2.1 Principe général des moindres carrés ordinaires

Avant de rentrer dans le cas général et dans des élaborations plus théoriques, on peut commencer par considérer un exemple simple dans lequel on examine la régression linéaire par la méthode des moindres carrés ordinaires du salaire horaire \(Y\) (en $ par heure) sur l’éducation \(X\) (en années passées dans le système scolaire) dans la population des salariés étatsuniens. Plus précisément, on estime cette régression à partir de données issues du Current Population Survey (CPS), une enquête statistique par sondage conduite par le Bureau of Census étatsunien, qui peut être regardée comme un analogue de l’Enquête Emploi en France. Dans la quasi-totalité des exemples de ce chapitre, on s’intéresse à la vague de mai 1985 de cette enquête, et on considère un extrait restreint à 534 salariés.

Effectuer cette régression permet de récupérer :

• pour chaque individu, une valeur du salaire prédit à partir de son niveau d’éducation \(\hat{Y}\) ;
• pour chaque individu, un terme résiduel \(\epsilon\) qui correspond à la différence entre la valeur prédite \(\hat{Y}\) et la valeur réalisée du salaire \(Y\) ;
• deux coefficients réels \(\alpha\) et \(\beta\) tels que \(\hat{Y}=\alpha + X\beta\), c’est-à-dire deux coefficients qui permettent d’exprimer la valeur prédite du salaire comme une fonction affine de l’éducation.

De surcroît, le terme résiduel possède deux propriétés importantes :

• il est nul en moyenne dans la population ;
• il n’est pas corrélé à l’éducation.

Le fragment de code suivant permet de vérifier empiriquement ces propriétés à partir des données du CPS, en examinant la régression estimée par la fonction lm.

library(AER,
        quietly=TRUE)
library(data.table,
        quietly=TRUE)
library(ggplot2,
        quietly=TRUE)

#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)

#On estime la régression du salaire horaire sur l'éducation
reg_wage_educ<-lm(wage~education,
                  data=CPS)

#On peut en lire les coefficients
reg_wage_educ

## 
## Call:
## lm(formula = wage ~ education, data = CPS)
## 
## Coefficients:
## (Intercept)    education  
##     -0.7460       0.7505

#On crée les variables qui correspondent à la décomposition, c'est-à-dire les
# valeurs prédites du salaire d'une part, les termes résiduels d'autre part
CPS$predi_wage<-reg_wage_educ$fitted.values
CPS$resid_wage<-reg_wage_educ$residuals

#On peut vérifier que la somme des deux variables est bien égale au salaire
all.equal(CPS$predi_wage+CPS$resid_wage,
          CPS$wage)

## [1] TRUE

#On peut vérifier que la valeur prédite du salaire est bien une fonction affine
# de l'éducation, qui peut s'écrire à l'aide des coefficients de la régression
all.equal(CPS$predi_wage,
          reg_wage_educ$coefficients["(Intercept)"]+
           CPS$education*
            reg_wage_educ$coefficients["education"])

## [1] TRUE

#On peut vérifier que la moyenne des résidus est nulle
all.equal(mean(CPS$resid_wage),
          0)

## [1] TRUE

#On peut aussi vérifier que les résidus ne sont pas corrélés à l'éducation
all.equal(cov(CPS$resid_wage,
              CPS$education),
          0)

## [1] TRUE

#On rajoute juste un peu de bruit à la variable d'éducation pour faciliter la 
# visualisation quand il y a plusieurs salariés avec le même niveau
# d'éducation
CPS$jitter_education<-
  CPS$education+
  (table(CPS$education)[as.character(CPS$education)]>1)*
  rnorm(nrow(CPS),sd=0.3)

#Visualisation

#Le fond commun aux deux panneaux : le nuage de points
nuage<-ggplot(data=CPS,
              aes(x=education,
                  y=wage))+
  geom_point(color="black",
             size=5,
             alpha=0.2,
             aes(x=jitter_education))+#nuage de points
  theme_classic()+#supprime l'arrière-plan gris par défaut
  coord_cartesian(ylim=c(-5,30))+#choix d'échelle des axes
  ylab("Salaire horaire ($ par heure)")+#titre des axes
  xlab("Années d'éducation")+
  theme(text=element_text(size=32),#taille du texte
        strip.text.x = element_text(size=32),
        panel.grid.minor = element_line(colour="lightgray",
                                        linewidth=0.01),#grille de lecture
        panel.grid.major = element_line(colour="lightgray",
                                        linewidth=0.01))

#Visualisation du nuage
nuage

#Visualisaton de la décomposition
nuage+geom_segment(aes(xend=jitter_education,
                       yend=wage,
                       x=jitter_education,
                       y=reg_wage_educ$coefficients["(Intercept)"]+
                         reg_wage_educ$coefficients["education"]*
                         jitter_education),
                   linewidth=0.001,
                   arrow = arrow(length = unit(0.5, "cm")))+
  geom_line(color="red",
            size=3,
             aes(x=jitter_education,
                 y=reg_wage_educ$coefficients["(Intercept)"]+
                   reg_wage_educ$coefficients["education"]*
                   jitter_education))

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.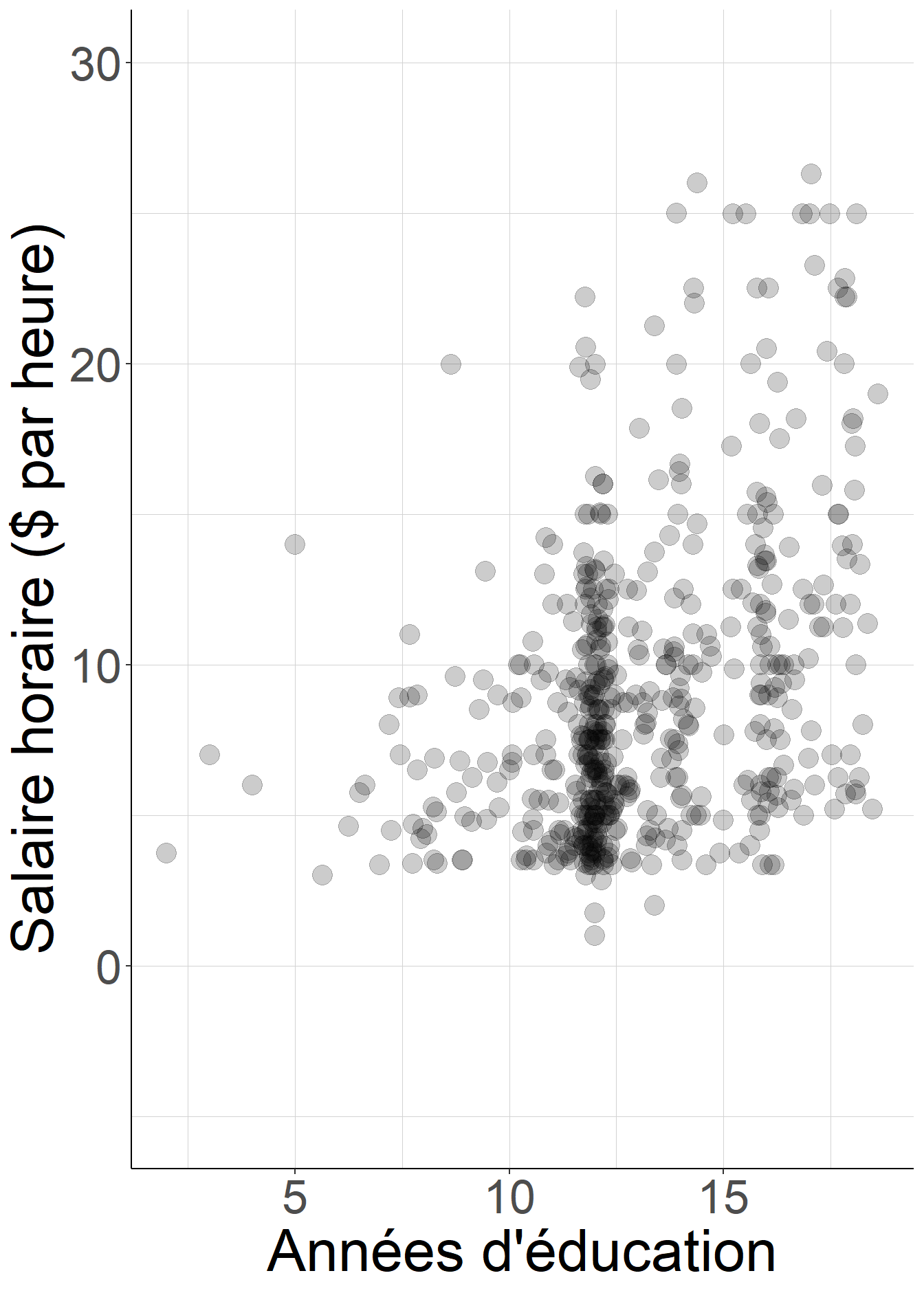

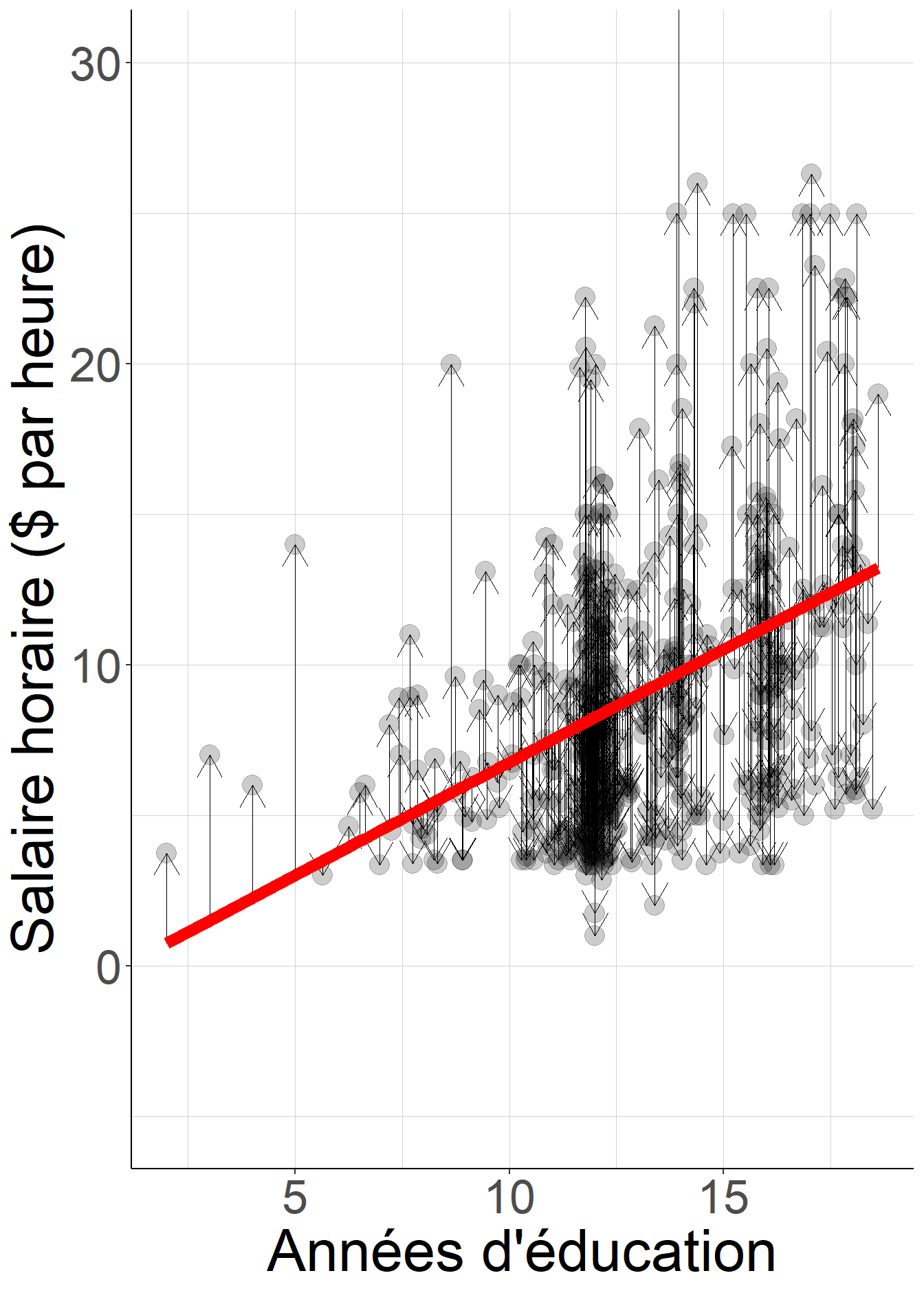
Figure 2.1: La régression linéaire par les moindres carrés décompose le salaire horaire, représenté par les points noirs, en une fonction affine de l’éducation, représentée par la droite rouge, et un terme résiduel de moyenne nulle et non-corrélé à l’éducation représenté par les flèches noires.

Tout cela peut se généraliser sous la forme d’une définition un peu plus abstraite.

Définition

La régression linéaire par les moindres carrés ordinaires d’une variable aléatoire réelle \(Y\) sur une variable aléatoire \(X\) possiblement multidimensionnelle définies sur la même expérience aléatoire est la décomposition de \(Y\) en la somme d’une fonction affine de \(X\) et d’un terme résiduel d’espérance nulle et non-corrélé à \(X\).

Formellement, la définition précédente affirme que si \(X\) et \(Y\) sont deux variables aléatoires réelles, \(X\) étant possiblement multidimensionnelle, définies sur la même expérience aléatoire, et si la matrice de variance-covariance de \(X\) est inversible³, alors la régression linéaire par les moindres carrés ordinaires consiste à chercher un réel \(\alpha\), un vecteur \(\beta\) dans \(\mathbb{R}^d\) et une variable aléatoire \(\epsilon\) définie sur la même expérience aléatoire que \(X\) et \(Y\) tels que : \[\left\{\begin{array}{l} Y = \alpha + X' \beta + \epsilon \\ \mathbb{E}[\epsilon] = 0 \\ \mbox{Pour tout }i \mbox{ dans }\{1, \dots, d\},\;\mathcal{C}(X_i,\epsilon)=0 \end{array}\right.\]

Pour un rappel sur l’approche en termes de variable aléatoire, se référer à 1.2. Pour revenir sur la définition de l’espérance \(\mathbb{E}\), voir 1.3.2. Enfin, la covariance \(\mathcal{C}\), et la corrélation sont définies en 1.3.5.

Définition

On appelle souvent le réel \(\alpha\) et les réels \(\beta_1\) à \(\beta_d\) les coefficients de la régression linéaire \(Y\) sur \(X\). La variable \(Y\) est souvent appelée variable dépendante, ou encore variable endogène. Les variables \(X_1\) à \(X_d\) sont souvent appelées variables indépendantes, régresseurs, ou variables exogènes, ou encore covariables. La variable aléatoire \(\epsilon\) est selon les contextes appelées résidu, choc idiosyncratique ou encore terme d’erreur. On appelle souvent la variable aléatoire \(\hat{Y}:=\alpha + X'\beta\) valeur prédite. Enfin, il est courant d’appeler l’équation \(Y=\alpha + X'\beta + \epsilon\) modèle de régression linéaire.

À retenir

Cette décomposition existe et est unique dés lors que la matrice de variance-covariance de \(X\) est inversible.

La preuve de cette proposition est détaillée à l’Annexe A.2⁴.

Lorsque \(X\) est multdimensionnelle de dimension \(d>1\), le terme \(X'\beta\) correspond au produit matriciel de la transposée⁵ de \(X\), c’est-à-dire la variable aléatoire à valeurs dans l’espace des matrices lignes de taille \(1 \times d\) \((X_1 \dots X_d)\) par le vecteur \(\beta\). Ce produit matriciel est tout simplement égal à la somme \(\sum_{i=1}^d X_i \beta_i\)⁶.

Remarque

En examinant l’exemple empirique construit à partir des données du CPS, on fait implicitement la confusion entre le paramètre \(\beta\) défini par le problème des moindres carrés ordinaires, qui est un paramètre défini par des espérances, et donc des quantités qui portent sur la population entière, et l’estimation de ces paramètres à partir de données observées dans une enquête portant sur un échantillon fini. Le lien entre ces deux quantités est très semblable à celui qui existent entre moyenne empirique et espérance et sera clarifié en 2.9.

Pour une discussion du lien entre espérance et moyenne empirique, voir 1.3.2 et 1.3.6.

Avertissement

L’existence et l’unicité de la décomposition fournie par le régression linéaire par les moindres carrés ordinaires ne dépendent pas de la structure causale du problème

En d’autres termes, quelles que soient les variables aléatoires \(X\) et \(Y\), pourvu que la condition d’inversibilité soit respectée, une telle décomposition est toujours possible et ne préjuge pas de ce que \(X\) puisse être interprétée comme une cause de \(Y\) ou non.

Avertissement

La validité de cette proposition ne dépend pas non plus de la loi de la variable dépendante \(Y\) ou des variables indépendantes \(X\), pour autant que l’hypothèse d’inversibilité soit respectée.

Ce résultat est ainsi tout aussi bien valable que \(Y\) soit une variable dichotomique à valeurs dans \(\{0, 1\}\), une variable discrète dont les valeurs sont des entiers naturels, une variable dont la distribution est continue…

---

3. Une matrice carrée \(A\) de taille \(d \times d\) est dite inversible lorsqu’il existe une matrice carrée \(B\) de taille \(d \times d\) telle que \(AB=BA=I_d\), où \(I_d\) est la matrice identité, c’est-à-dire la matrice carrée de taille \(d \times d\) dont tous les éléments diagonaux sont égaux à 1, et tous les éléments diagonaux sont égaux à 0. Cette matrice est unique, on l’appelle l’inverse de \(A\) et on la note en général \(A^{-1}\). Des résultats élémentaires d’algèbre linéaire montrent que \(A\) est inversible si et seulement si ses colonnes sont linéairement indépendantes, ou de façon équivalente si et seulement si ses lignes sont linéairement indépendantes.↩︎

4. La lectrice ou le lecteur attentif et rigoureux remarquera qu’en réalité l’existence et l’unicité de la fonction affine vérifiant les hypothèses des moindres carrés ordinaires est toujours assurée, et que c’est en fait l’unicité de l’écriture de cette fonction sous la forme \(\alpha + X'\beta\) qui est problématique lorsque la matrice de variance-covariance de \(X\) n’est pas inversible. Le premier exemple de la section 2.2 met ce fait en évidence en montrant que lorsque cette hypothèse n’est pas respectée, aussi bien la valeur prédite \(\hat{Y}\) que les résidus \(\epsilon\) associés à des solutions \((\alpha, \beta)\) différentes du problème sont en fait les mêmes.↩︎

5. La transposée d’une matrice de taille \(k \times l\) est la matrice de taille \(l \times k\) dont le coefficient à la \(i\)-ème ligne et à la \(j\)-ème colonne est égal au coefficient de la matrice de départ à la \(j\)-ème ligne et à la \(i\)-ème colonne. Ainsi, si \(x\) est une matrice colonne de taille \(d \times 1\), alors \(x'\) est une matrice ligne de taille \(1 \times d\).↩︎

6. Pour revoir la lecture du signe somme \(\sum\), se rendre en 1.1.2.↩︎