5.7 Quel rôle pour la régression linéaire ?
Parce que la régression linéaire par la méthode des moindres carrés ordinaires possède des liens très forts avec l’espérance conditionnelle, c’est-à-dire avec les valeurs prises par la moyenne de la variable dépendante dans des groupes définis par les valeurs des variables indépendantes, lorsque l’on considère la population d’intérêt tout entière et non seulement l’échantillon. C’est la raison pour laquelle elle peut être utilisée pour estimer les effets causaux moyens d’une intervention dans des situations empiriques où l’on peut justifier que lorsque l’on se place à l’intérieur de strates définies par les valeurs de certaines variables de conditionnement, l’assignation à l’intervention s’assimile à une expérience aléatoire contrôlée ou à une expérience naturelle.
Comme pour les approches passant par le score de propension, cela exige toutefois certaines précautions. Le reste de cette section vise à (i) montrer de quelle façon utiliser la régression linéaire pour estimer des effets causaux moyens et (ii) expliciter les précautions à prendre, au-delà de la justification de l’hypothèse d’indépendance conditionnelle qui assimile l’assignation à l’intervention à une expérience aléatoire stratifiée, pour évaluer la qualité de l’estimation de ces effets causaux moyens par régression linéaire.
5.7.1 Usage habituel de la régression linéaire
5.7.1.1 Cas des variables de conditionnement discrètes
On peut repartir de l’exemple de l’expérience aléatoire contrôlée défectueuse de Gerber et Green (2000) réanalysée par Imai (2005). Pour simplifier dans un premier temps la discussion, on va supposer comme on l’a fait auparavant que le seul problème dans la réalisation de cette expérience aléatoire contrôlée visant à évaluer l’effet d’un appel téléphonique incitant à voter sur la participation électorale tient à ce que la probabilité de recevoir un tel appel varie d’un quartier de New Haven à l’autre.
L’usage habituel de la régression linéaire dans ce cas serait de régresser la variable représentant le fait d’être allé voter en 1998 sur (i) la variable dichotomique qui représente le fait d’avoir reçu ou non l’appel et (ii) les variables dichotomiques représentant le fait d’habiter dans chacun des différents quartiers de New Haven.
La lectrice ou le lecteur qui garde en tête les résultats relatifs à la régression linéaire par les moindres carrés ordinaires se souvient que dans ce cas, le coefficient sur la variable représentant l’appel téléphonique est égal à la moyenne sur l’ensemble des quartiers de la différence de taux de participation électorale entre ceux qui ont reçu l’appel et ceux qui ne l’ont pas reçu à l’intérieur du même quartier, avec des poids qui donnent plus d’importance aux quartiers (i) dont la population est la plus grande et (ii) où la probabilité de recevoir un appel téléphonique est plus proche de 50% (voir 2.6.3 pour un rappel sur ce résultat).
Comme on suppose qu’à l’intérieur de chaque quartier, la situation peut bien s’assimiler à une expérience aléatoire contrôlée, ou à une expérience naturelle, la différence de taux de participation électorale entre ceux qui ont reçu l’appel et ceux qui ne l’ont pas reçu à l’intérieur d’un certain quartier identifier l’effet causal moyen de l’appel téléphonique sur la participation électorale dans ce quartier. Ainsi, le coefficient sur la variable représentant l’appel téléphonique dans la régression est égal à une moyenne d’effets causaux moyens spécifiques à chaque quartier. Ce coefficient a donc bien une interprétation causale.
La différence avec l’estimation naïve, ou bien celle que l’on obtient avec les techniques fondées sur le score de propension tient à ce que les poids avec lesquels on agrège ces effets causaux moyens spécifiques à chaque quartier ne sont pas les mêmes lorsque l’on passe par une régression linéaire. En effet, avec ces techniques on se contenterait de poids proportionnels à la taille de la population de chaque quartier, tandis que dans la régression linéaire le poids que l’on donne à un quartier dépend non seulement de sa population, mais aussi de la probabilité d’y recevoir un appel téléphonique.
Le fragment de code suivant permet d’examiner cet exemple à partir des données de Gerber et Green (2000) et Imai (2005), et montre bien que la différence entre les deux approches tient aux poids que l’on applique aux différents quartiers.
library(data.table)
library(ggplot2)
library(Matching)
#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)
#On estime le modèle de régression linéaire et on récupère le coefficient sur
# la variable représentant l'appel téléphonique
estimation_OLS<-lm(VOTED98 ~ PHN.C1 + WARD,
data=GerberGreenImai)$coefficients["PHN.C1"]
#Pour chaque quartier, on estime : la différence de taux de participation
# électorale entre ceux qui ont et ceux qui n'ont pas reçu l'appel téléphonique
# la taille du quartier et la probabilité d'y recevoir l'appel téléphonique
estimation_par_quartier<-GerberGreenImai[,
list(contraste_participation=
sum(PHN.C1*VOTED98)/
sum(PHN.C1)-
sum((1-PHN.C1)*VOTED98)/
sum(1-PHN.C1),
taille=.N,
proba_appel=sum(PHN.C1)/.N),
by=c("WARD")]
#On peut agréger ces différences de taux de participation avec des poids
# proportionnels à la taille du quartier et à la variance conditionnelle
# (1-proba_appel)*proba_appel
contraste_participation_agrege<-
estimation_par_quartier[!is.na(contraste_participation),
list(moyenne_effet_causal=
sum(taille*
(1-proba_appel)*proba_appel*
contraste_participation)/
sum(taille*
(1-proba_appel)*proba_appel))]
#On peut vérifier que cela permet bien de retrouver le coefficient portant sur
# la variable représentant l'appel téléphonique
all.equal(as.numeric(estimation_OLS),
as.numeric(contraste_participation_agrege))## [1] TRUE#On peut également estimer comme on le ferait spontanément l'effet causal moyen
# au niveau de New Haven prise toute entière
#La seule différence est que les poids sont seulement proportionnels à la
# taille de chaque quartier
ATE_New_Haven<-estimation_par_quartier[!is.na(contraste_participation),
list(moyenne_effet_causal=
sum(taille*
contraste_participation)/
sum(taille))]
#On peut tout mettre sur la même figure
#Pour visualiser les probabilités pour chaque quartier
ggplot(data=estimation_par_quartier[!is.na(contraste_participation)],
aes(x=proba_appel,
y=contraste_participation*100))+
geom_point(aes(size=taille/nrow(GerberGreenImai)),
alpha=0.5)+
theme_classic()+
scale_size(name="Part dans la \npopulation de \nNew Haven",
labels=scales::percent)+
geom_hline(yintercept = as.numeric(ATE_New_Haven)*100,
color="red",
size=1.5,
linetype="dashed")+
geom_hline(yintercept = as.numeric(estimation_OLS)*100,
color="red",
size=1.5)+
xlab("Probabilité de recevoir l'appel \ntéléphonique incitant à voter")+
ylab("Différence de taux de participation \nentre ceux qui ont reçu l'appel et \nles autres (en p.p.)")+
theme(text=element_text(size=16),#taille du texte
legend.title=element_text(size=12),
legend.text=element_text(size=12),
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
size=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
size=0.01))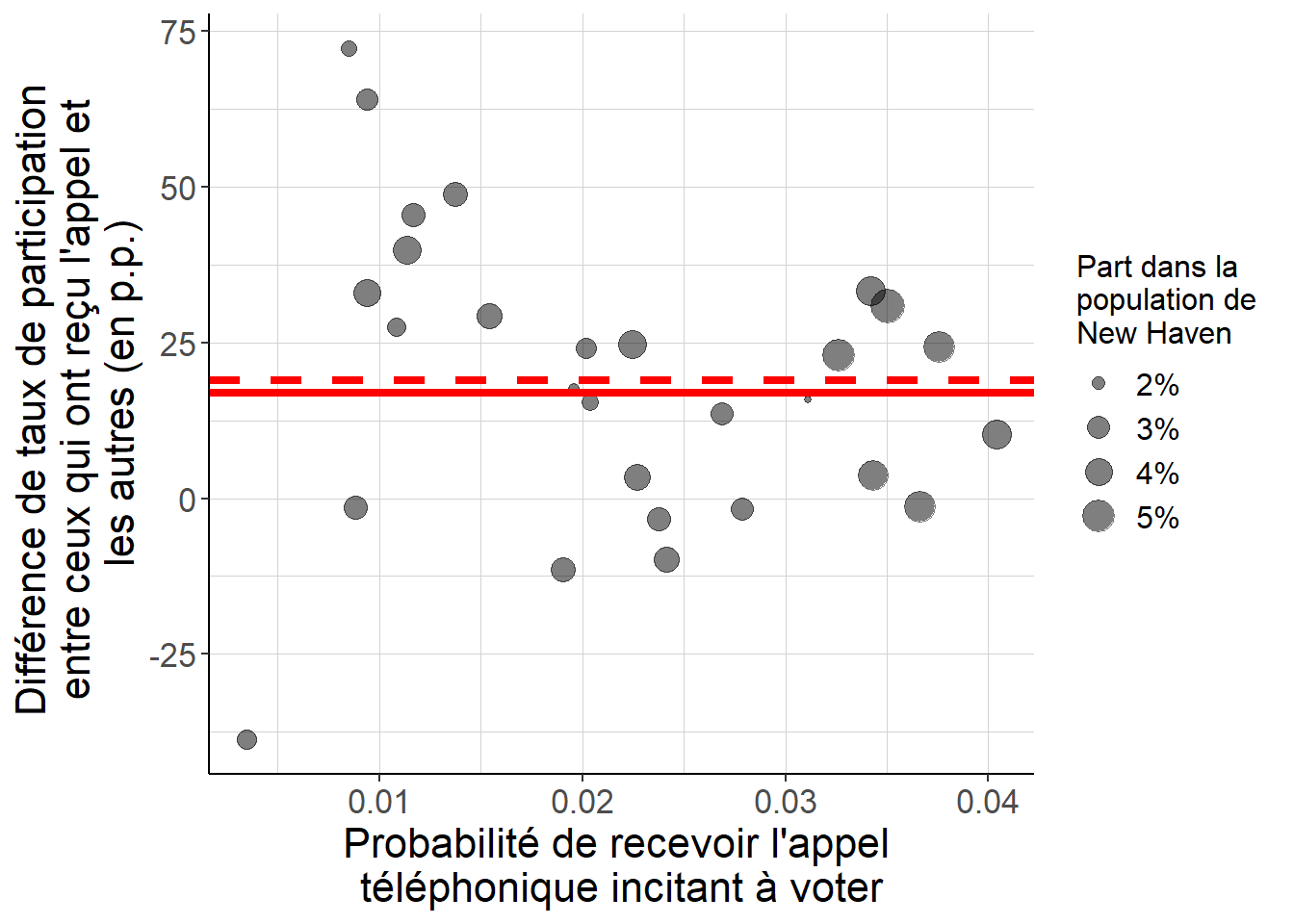
Figure 5.15: Lorsque l’on régresse en utilisant les moindres carrés ordinaires la participation électorale sur (i) la variable représentant le fait d’avoir reçu ou non l’appel téléphonique incitant à voter et (ii) toutes les variables dichotomiques représentant le fait d’habiter dans l’un ou l’autre des quartiers de New Haven, le coefficient sur la première variable, représenté par la droite horizontale rouge en trait plein, est égal à une moyenne des différences de taux de participation électorale entre ceux qui ont reçu l’appel et les autres à l’intérieur de chaque quartier, représentée par l’ordonnée de chacun des points. Les poids pour agréger ces différences sont proportionnels à (i) la part de chacun de ces quartiers dans la population de New Haven et (ii) un terme qui donne une plus grande importance aux quartiers dans lesquels la probabilité de recevoir un appel est plus proche de 50%, et est nul lorsqu’elle vaut 0 ou 100%. Les poids qui interviennent dans ce calcul sont la seule différence avec la façon dont on estimerait l’effet causal moyen à l’échelle de tout New Haven sous les seules hypothèses d’indépendance conditionnelle et de support commun, représenté par la droite rouge en traits pointillés. Dans ce second cas, on n’utiliserait que des poids proportionnels à la part de chaque quartier dans la population de New Haven, et la probabilité de recevoir l’appel n’interviendrait pas.
5.7.1.2 Cas général
Le résultat précédent tient en fait à ce que, lorsque l’on régresse la variable représentant le fait d’avoir reçu ou non l’appel téléphonique incitant à voter sur toutes les variables représentant le fait d’habiter ou non dans chacun des quartiers de New Haven, les valeurs prédites par cette régression sont égales à la part des habitants de chaque quartier qui a reçu un appel téléphonique, et s’identifie donc aux vraies valeurs du score de propension : on retombe sur le cas de la régression saturée (voir 2.6.2 et 5.5.2.1). C’est en fait le cas chaque fois que les variables de conditionnement que l’on inclut dans la régression peuvent se ramener à des variables dichotomiques décrivant des strates qui (i) recrouvrent tout l’espace des possibles et (ii) sont mutuellement exclusives.
Mais lorsque l’on se trouve dans une telle situation, le passage par l’estimation naïve où l’on commence par calculer les écarts moyens au sein de chaque strate, avant d’agréger ces écarts moyens en en prenant la moyenne avec des poids proportionnels à la taille de chaque strate n’est pas coûteux : il n’y a donc finalement pas vraiment de raison de passer par une régression linéaire. Il faut donc étudier le cas général qui est relativement plus difficile.
On dispose en fait d’un résultat théorique qui dit que, lorsque l’on régresse la variable d’intérêt sur la variable dichotomique représentant l’intervention d’une part, et les variables de conditionnement d’autre part, le coefficient sur la première est la somme de deux termes :
- une moyenne d’effets causaux moyens spécifiques à chaque strate, avec des poids proportionnels à la taille de chaque strate mais négatifs si et seulement si les valeurs du score de propension estimées à partir d’une régression linéaire sont plus grandes que 1, et ;
- un terme qui ne dépend pas des effets causaux de l’intervention, et qui est nul :
- si les valeurs estimées du score de propension à partir d’une régression linéaire coïncident avec les vraies valeurs du score de propension, ou bien si ;
- si, la moyenne des valeurs potentielles de la variable d’intérêt en l’absence d’intervention dans chacune des strates définies par la valeur exacte des variables de conditionnement s’identifie à la valeur prédite de cette variable à partir d’une régression linéaire de celle-ci sur les variables de conditionnement.
La lectrice ou le lecteur intéressé trouvera en Annexe A.16 une preuve formelle de ce résultat.
Cette interprétation du coefficient renvoyé par la régression linéaire comme une somme de deux termes a deux implications lorsque l’on cherche à utiliser cette approche pour estimer des effets causaux moyens.
- Dans le premier terme, on veut éviter au maximum de mettre un poids négatif sur certaines strates. En effet, ces poids négatifs ont comme conséquence fâcheuse que le coefficient peut se trouver en dehors de l’intervalle défini par les valeurs extrêmes des effets causaux moyens spécifiques à chaque strate. En particulier, lorsque l’on met un poids négatif sur certaines strates, on peut se retrouver dans la situation où le coefficient est négatif (respectivement positif) alors que tous les effets causaux moyens spécifiques à chaque strate sont positifs (respectivement négatifs).
- On veut que le deuxième terme, qui n’a pas d’interprétation causale, soit nul. Pour cela, il faut que l’on trouve une spécification telle que ou bien le score de propension puisse être estimé par une régression linéaire, ou bien la moyenne de la variable d’intérêt dans chaque strate, dans le groupe qui ne fait pas l’objet de l’intervention, puisse aussi être très bien approximée par une régression linéaire.
Les deux points justifient de se pencher sur la qualité de l’estimation du score de propension par régression linéaire. En effet, si l’on parvient à une estimation de bonne qualité à partir d’une régression linéaire, alors on s’assure que :
- il n’y a pas de poids négatifs dans le premier terme, et donc l’interprétation causale de celui-ci est raisonnable, et ;
- les valeurs du score de propension estimées à partir d’une régression linéaire sont très proches des vraies valeurs du score de propension, de sorte que le second terme est nul ou négligeable.
Par conséquent, on peut bien faire une interprétation causale du coefficient qui porte sur la variable représentant l’intervention.
L’intérêt de se pencher sur l’estimation du score de propension par une régression linéaire, plutôt que sur la validité de l’approximation linéaire de la variable d’intérêt dans le groupe non-traité est que l’on dispose déjà pour ce faire des outils que l’on a étudiés précédemment : on va tout bonnement évaluer de nouveau l’hypothèse de support commun d’une part, et la propriété équilibrante du score de propension estimé d’autre part.
5.7.1.3 Un exemple empirique
Le fragment de code suivant propose de faire ce travail sur l’exemple tiré de Gerber et Green (2000) et Imai (2005). Comme pour les exemples précédents, on estime dans un premier temps le score de propension, cette fois-ci à partir d’une régression linéaire. On représente ensuite la distribution des scores de propension dans les deux groupes définis par le fait d’avoir reçu ou non un appel téléphonique incitant à voter.
library(data.table)
library(ggplot2)
library(Matching)
#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)
#On estime le score de propension avec une régression linéaire
pscore_estimates_OLS<-lm(PHN.C1 ~ PERSONS +
WARD +
AGE +
MAJORPTY +
VOTE96.0 +
VOTE96.1 +
NEW +
AGE2 +
PERSONS*VOTE96.0 +
PERSONS*NEW,
data=GerberGreenImai)$fitted.values
#On remet ce score de propension estimé dans la table initiale
GerberGreenImai<-cbind(GerberGreenImai,
pscore_estimates_OLS)
#On peut regarder rapidement la distribution des valeurs ainsi estimées du
# score de propension
summary(GerberGreenImai$pscore_estimates_OLS)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.01793 0.01102 0.02178 0.02281 0.03385 0.07880#On peut commencer par regarder la distribution du score de propension
# dans chacun des deux groupes définis par le fait d'avoir reçu ou non
# un appel téléphonique
ggplot(data=GerberGreenImai,
aes(x=pscore_estimates_OLS,
fill=factor(PHN.C1, levels=c("1","0")),
color=factor(PHN.C1, levels=c("1","0"))))+
geom_histogram(binwidth = 0.005,
alpha=0.5,
aes(y=after_stat(density)*0.005),
position="identity")+
theme_classic()+
xlab("Score de propension estimé \n par régression linéaire")+
ylab("Fréquence")+
scale_colour_grey(start=0.1,
end=0.4,
labels=c("Oui",
"Non"),
name="A reçu un appel téléphonique \nencourageant à voter")+
scale_fill_grey(start=0.1,
end=0.9,
labels=c("Oui",
"Non"),
name="A reçu un appel téléphonique \nencourageant à voter")+
scale_y_continuous(labels = scales::percent)+
scale_x_continuous(labels = scales::percent)+
coord_cartesian(xlim=c(0,0.15))+
theme_classic()+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
legend.title=element_text(size=12),
legend.text=element_text(size=12),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))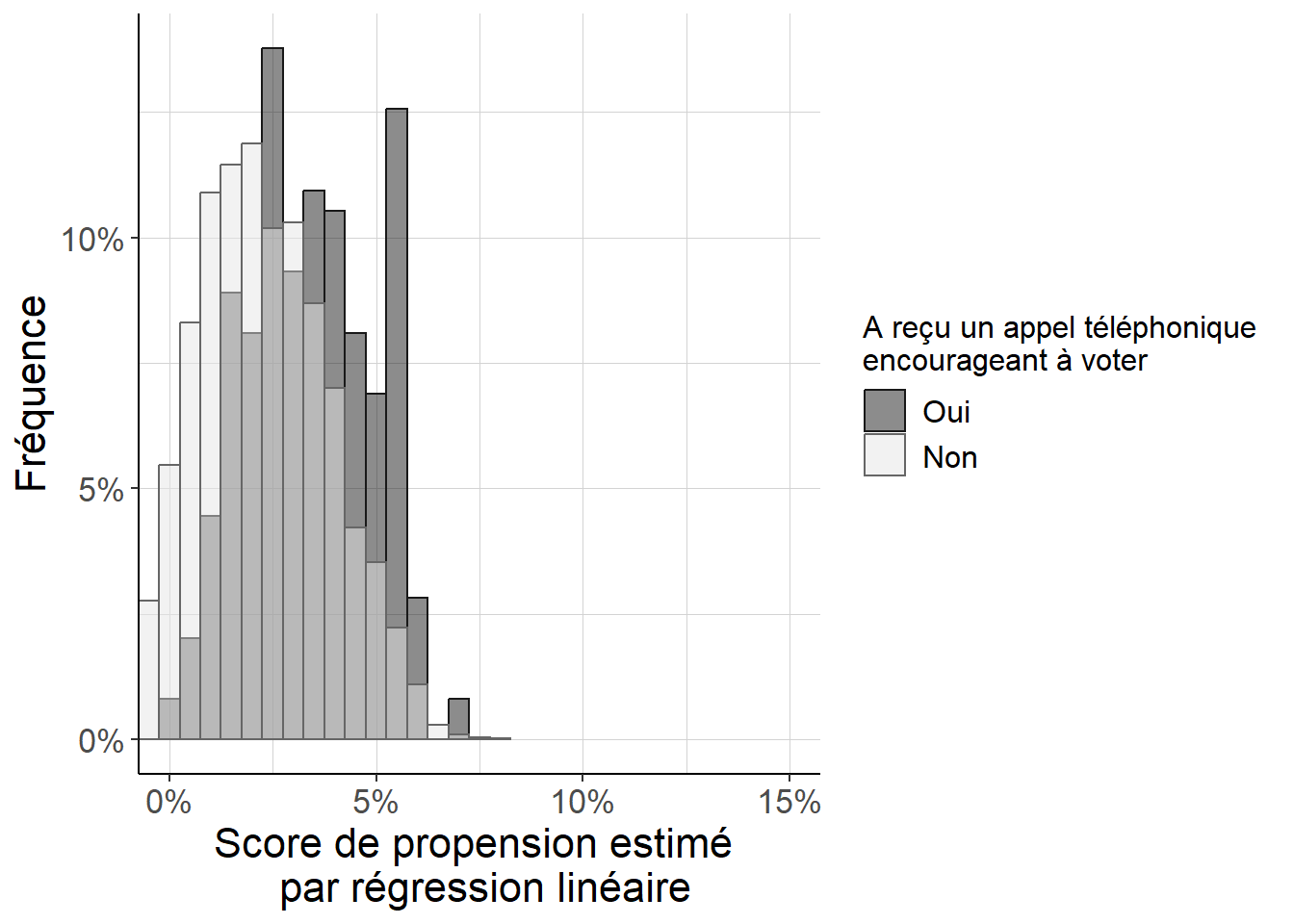
Figure 5.16: Histogramme répliquant Imai (2005) (figure 8), dans le cas d’un score de propension estimé par régression linéaire. Parce que l’on est, en dépit de ses défauts, dans un cas proche d’une expérience aléatoire contrôlée avec une faible probabilité de recevoir un appel téléphonique appelant à voter, on peut voir que (i) les scores de propension sont faibles pour tous les individus, et (ii) les différences entre individus ayant reçu ou n’ayant pas reçu d’appel téléphonique restent contenues. Cependant, on voit aussi que le score de propension est également en général plus important pour les individus ayant reçu un appel téléphonique que pour les autres. Un dernier trait potentiellement important ici est que l’on note quelques valeurs négatives du score de propension estimé : cela signale que l’approximation linéaire n’est pas parfaite.
Une fois que l’on a examiné l’hypothèse de support commun, il faut s’intéresser à la propriété équilibrante du score de propension estimé par régression linéaire. La façon la plus simple de procéder est de le faire par stratification, même si on pourrait tout à fait choisir de procéder différemment, par exemple par appariement ou par repondération. On utilise pour ce faire toutes les fonctions que l’on a créées en 5.6.
#On définit les strates à partir des quintiles de la distribution du score de
# propension estimé par régression linéaire
quintiles_pscore_OLS<-
quantile(GerberGreenImai$pscore_estimates_OLS,
probs=0.2*c(1:4))
GerberGreenImai[,
strates_pscore_OLS:=
findInterval(x=pscore_estimates_OLS,
vec=quintiles_pscore_OLS)]
#Au sein de chacune de ces strates, on va comparer du point de vue de la valeur
# des variables de conditionnement les individus selon qu'ils ont ou qu'ils
# n'ont pas reçu un appel téléphonique, et on va réagréger ces écarts avec
# des poids proportionnels à la taille de chaque strate dans la population
# (ici comme les strates sont définies par les valeurs des quintiles elles ont
# toutes le même poids).
#On va aussi comparer cet écart estimé via la stratification à l'écart brut
# sans stratification
#On applique cette fonction aux variables de conditionnement, d'abord sans
# stratification, ensuite avec la stratification
#On définit les variables de conditionnement sur lesquelles on va tester
# la propriété équilibrante du score de propension
variables_conditionnement<-c("PERSONS",
"AGE",
"MAJORPTY",
"VOTE96.0",
"VOTE96.1",
"NEW")
#Sans stratification : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement
contrastes_bruts<-GerberGreenImai[,
lapply(X=.SD,
FUN=function(x){
list(
diff_moy(
variable=x,
groupe_intervention=PHN.C1),
sqrt(0.5*var(x)))
}),
.SDcols=variables_conditionnement]
contrastes_bruts[,
stat:=c("diff_moy",
"spread")]
contrastes_bruts<-melt(contrastes_bruts,
variable.name="variable",
value.name="valeur",
id.vars="stat")
#Avec stratification
#On commence par calculer la différence moyenne dans chaque strate
contrastes_par_strates_OLS<-
GerberGreenImai[,
lapply(
X=.SD,
FUN=function(x){
diff_moy(variable=x,
groupe_intervention=
PHN.C1)
}),
.SDcols=variables_conditionnement,
by=c("strates_pscore_OLS")
]
#Ensuite on prend la moyenne de ces différences moyennes (comme on a défini
# les strates à partir des quintiles, elles ont toutes le même poids dans la
# population et on n'a pas besoin de spécifier les poids)
contrastes_agreges_stratifies_OLS<-
contrastes_par_strates_OLS[,
lapply(X=.SD,
mean),
.SDcols=variables_conditionnement]
contrastes_agreges_stratifies_OLS[,
stat:="diff_moy"]
contrastes_agreges_stratifies_OLS<-
melt(contrastes_agreges_stratifies_OLS,
id.vars="stat",
value.name="valeur",
variable.name="variable")
#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
contrastes_stratification_OLS<-
contrastes_propre(contrastes_bruts,
contrastes_agreges_stratifies_OLS)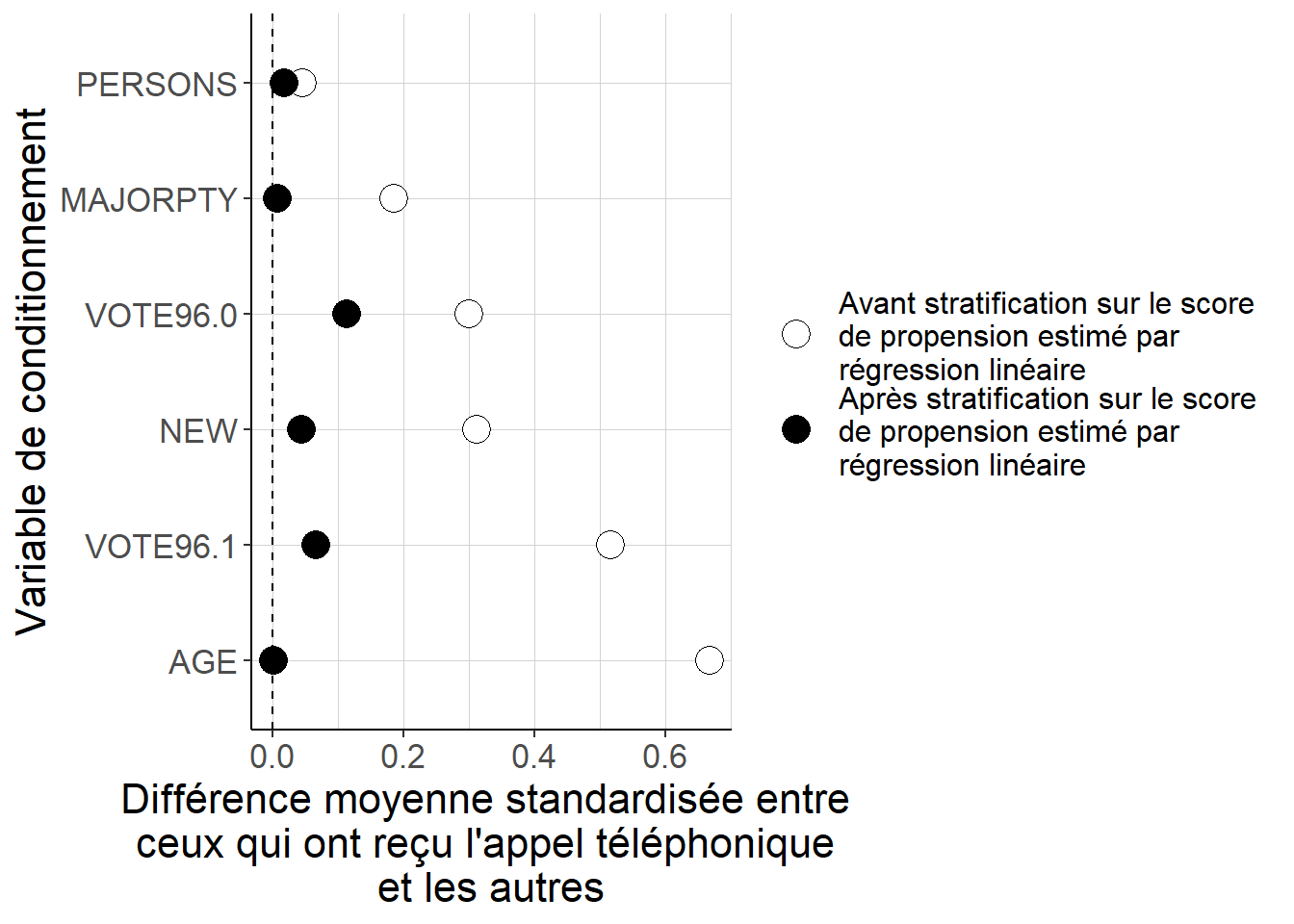
Figure 5.17: Alors que les différences quant aux valeurs des variables de conditionnement entre les individus qui ont reçu l’appel téléphonique et les autres peuvent être importantes lorsque l’on considère les données brutes, constituer 5 strates à partir des quintiles des valeurs du score de propension estimées à partir d’une régression linéaire permet de réduire de façon importante ces écarts. Cela suggère que ces valeurs estimées du score de propension permettent de mieux équilibrer les deux groupes du point de vue de ces variables de conditionnement. Cependant, il reste des différences importantes sur certaines dimensions qui signalent que l’équilibrage n’est pas parfait. Ainsi, la spécification que l’on a choisie n’est peut-être pas la plus adaptée et pourrait sans doute être améliorée.
Une fois passées ces étapes où l’on examine la qualité de l’estimation du score de propension par régression linéaire, on peut procéder à l’estimation des effets causaux moyens de l’appel téléphonique sur la participation électorale en procédant simplement à la régression que l’on envisageait de faire depuis le début.
#On estime la régression à proprement parler
effet_causal_OLS<-lm(VOTED98 ~
PHN.C1 +
PERSONS +
WARD +
AGE +
MAJORPTY +
VOTE96.0 +
VOTE96.1 +
NEW +
AGE2 +
PERSONS*VOTE96.0 +
PERSONS*NEW,
data=GerberGreenImai)$coefficients["PHN.C1"]
effet_causal_OLS## PHN.C1
## 0.09497093Au total, même si l’estimation du score de propension par régression linéaire n’est pas parfaite, on n’est pas ici dans un cas catastrophique lorsque l’on compare la situation à celle que l’on obtient par exemple en passant par un modèle logit, comme on le faisait en 5.6. Cela explique vraisemblablement pourquoi les résultats obtenus quand aux effets causaux moyens de l’appel téléphonique incitant à voter sur la participation électorale ne sont pas très différents de ce que l’on avait obtenu avec les méthodes fondées de façon plus évidente sur le score de propension.
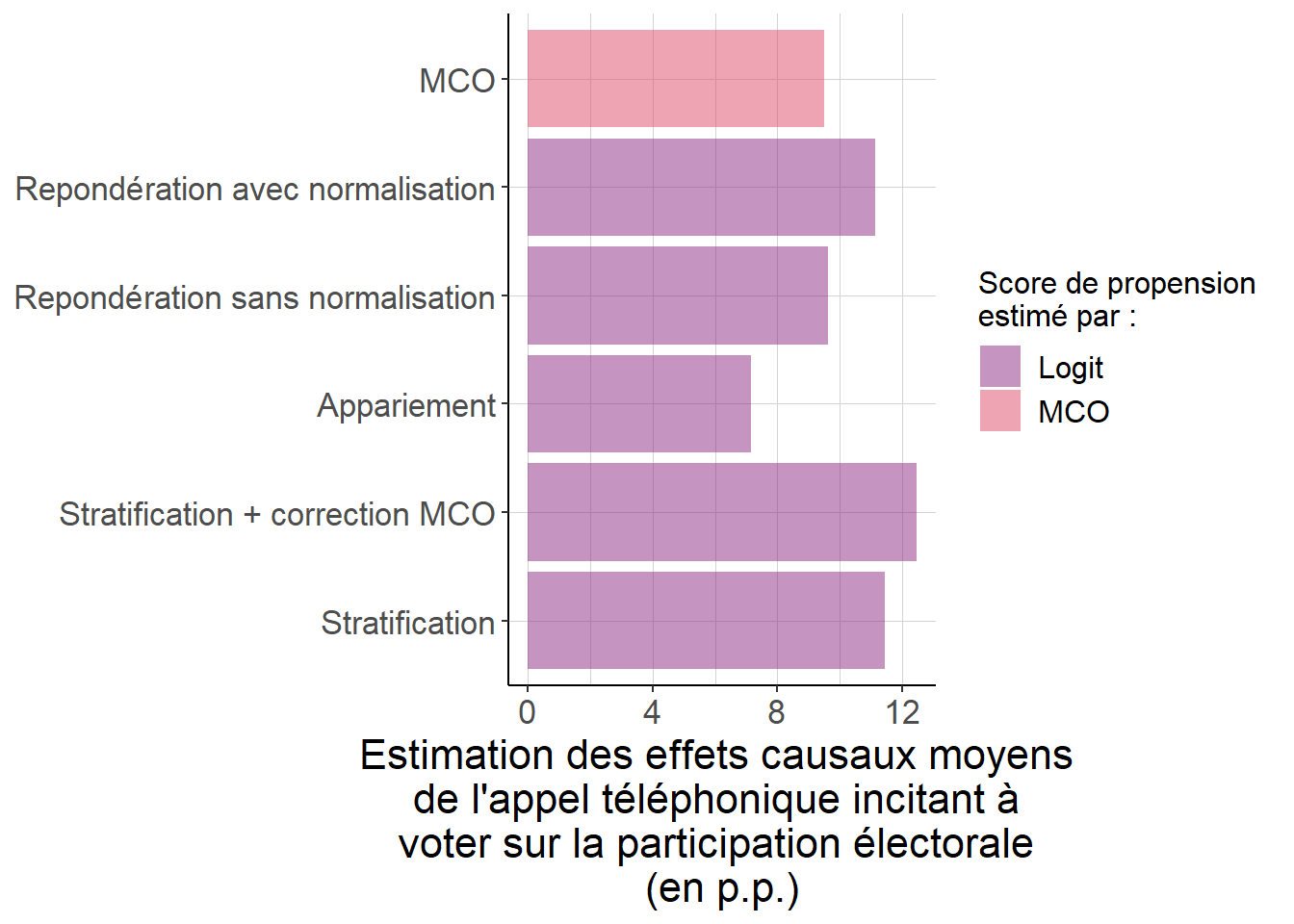
Figure 5.18: Les résultats obtenus en passant par une régression linéaire sont ici assez comparables à ceux que l’on obtient lorsque l’on passe par les techniques fondées explicitement sur le score de propension. Cela tient au fait que l’approximation linéaire pour le score de propension est peut-être raisonnable, comme en témoignent les figures évaluant la validité de l’hypothèse de support commun (figure 5.16) et celle se penchant sur la propriété équilibrante du score de propension estimé par régression linéaire (figure 5.17). Il faut toutefois faire attention au fait que la quantité estimée n’est pas tout à fait la même : les autres techniques donnent à chaque strate un poid qui ne dépend que de sa taille, alors que la régression linéaire donne aux strates une importance qui dépend de leur taille, mais aussi de ce que la probabilité d’y recevoir l’appel téléphonique est plus ou moins proche de 50%.
5.7.2 Pourquoi utiliser une régression linéaire ?
Au total, sous les hypothèses d’indépendance conditionnelle et de support conditionnel, l’approche habituelle par régression linéaire renvoie donc à des quantités estimées qui ont une interprétation causale dés lors que l’estimation du score de propension par une régression linéaire renvoie des valeurs suffisamment proches des vraies valeurs du score de propension, ce que l’on peut regarder au moins dans un premier temps en évaluant la qualité de l’équilibrage lorsque l’on utilise ces valeurs estimées du score de propension. Comme évaluer cela suppose finalement de faire le même travail d’évaluation de la qualité du score de propension que pour les autres approches, on peut légitimement se demander quel peut être l’intérêt de recourir à cette technique. Il y a à cela au moins deux réponses
5.7.2.1 Une inférence facilitée
Une première bonne raison de recourir à l’approche par régression linéaire est que l’inférence, c’est-à-dire la quantification de l’incertitude quant à l’estimation y est un sujet très balisé (voir 2.9). Ainsi, bien que cela ne soit pas toujours d’une simplicité enfantine, les outils permettant d’évaluer l’incertitude sur les résultats que l’on obtient ainsi sont en général facilement disponibles dans la plupart des logiciels statistiques, et pas trop difficiles à implémenter lorsque cela n’est pas le cas.
Cela n’est pas toujours vrai des approches fondées plus explicitement sur le score de propension. Ainsi, certains auteurs privilégient des approches où l’incertitude découle du fait que l’on examine un échantillon de taille finie extrait d’une population beaucoup plus grande, tandis que d’autres privilégient des approches qui reviennent à supposer que l’on travaille à partir de données exhaustives sur la population, mais que l’incertitude découle du caractère aléatoire de l’assignation des différents individus à l’intervention (Imbens (2015)). De plus, certaines approches courantes pour évaluer l’incertitude ne peuvent être appliquées lorsque l’on a recours aux techniques d’appariement sur les plus proches voisins (Abadie et Imbens (2008)). Au total, il s’agit là de questions moins balisées que l’inférence sur les régressions linéaires, et cela peut justifier de s’en tenir, au moins dans un premier temps, à une approche par régression linéaire. C’est ainsi la recommandation formulée par Angrist et Pischke (2008).
5.7.2.2 Une estimation plus efficace
Par rapport aux autres techniques fondées plus explicitement sur le score de propension, un des désavantages de l’usage de la régression linéaire pour estimer des effets causaux tient à ce que la quantité estimée n’est pas définie comme les effets causaux moyens de l’intervention pour toute la population. Au contraire, elle est définie comme une moyenne d’effets causaux moyens spécifiques à chaque strate correspondant à la valeur des variables de conditionnement, avec des poids qui reflètent non seulement la taille de chacune de ces strates, mais aussi dépendent aussi, lorsque l’approximation linéaire pour l’estimation du score de propension est valable, de la probabilité de faire l’objet de l’intervention dans chaque strate d’une façon qui donne une plus grande importance aux strates dans lesquelles cette probabilité est proche de 50%, et une importance beaucoup plus faible à celles dans lesquelles cette part est proche de 0 ou 100%.
Si cela peut sembler décevant à première vue, cela n’est pas nécessairement un défaut. En effet, ce qui importe dans l’évaluation des effets causaux de l’intervention est non seulement de produire une évaluation non-biaisée, mais aussi une évaluation qui soit assez précise pour être réellement informative. En fait, Goldsmith-Pinkham, Hull et Kolesár (2021) montrent que, parmi toutes les moyennes pondérées d’effets causaux moyens spécifiques à chaque strate que l’on peut construire, celle que l’on peut estimer le plus précisément possible est exactement celle qui est estimée par la régression linéaire lorsque l’approximation linéaire pour le score de propension est valable.
Dans la mesure où les effets causaux moyens de l’intervention sur toute la population est aussi une moyenne pondérée d’effets causaux moyens spécifiques à chaque strate – tout bonnement avec des poids proportionnels à la taille de chaque strate – ce résultat n’est pas anodin. Il signifie que l’estimation de ces effets causaux moyens sera toujours moins précise que celle que l’on obtient en passant par une régression linéaire. Ainsi, dans le cas où l’approche par régression linéaire renvoie des résultats relativement imprécis, on sait d’avance et sans même avoir besoin de passer par une des autres techniques que les données utilisées seront très peu informatives quant aux effets causaux moyens de l’intervention dans toute la population.
Enfin, il est tout de même possible par une utilisation astucieuse des régressions linéaires d’estimer les effets causaux moyens d’une intervention sous l’hypothèse d’indépendance conditionnelle et de support commun. L’Annexe B.5 développe ce point un peu plus précisément.