4.1 Pour commencer : les admissions à Berkeley sont-elles biaisées selon le genre ?
Ce chapitre débute par un retour sur un exemple historique, l’étude de l’éventuel biais de genre de la procédure d’admission en graduate school à l’Université de Californie à Berkeley dans les années 1970. Dans cet article, Bickel, Hammel et O’Connell (1975) mobilisent des données administratives qui correspondent aux remontées de décisions d’admission à Berkeley à l’automne 1973. La question qu’ils posent, à savoir l’existence de pratiques discriminatoires sexistes dans la procédure d’admission est bien une question causale. En effet, elle revient essentiellement à se demander si, face à une candidature données, le jury d’admission prendrait la même décision si cette candidature émanait d’un candidat de l’autre sexe.
L’approche naïve de la question consiste à considérer la population de l’ensemble des candidatures déposées à l’université pour cette session, et à contraster la part d’admis selon le sexe. Le fragment de code suivant reprend cette approche, sur un extrait des données utilisées par Bickel, Hammel et O’Connell (1975) restreint aux six départements les plus importants de l’université.
library(datasets)
library(data.table)
sexbias_dat<-data.table(UCBAdmissions)
#On compare la part d'admis parmi les candidats selon le sexe
sexbias_dat[,
list(part=sum(as.numeric(Admit=="Admitted")*
N)/
sum(N)*
100),
by="Gender"]## Gender part
## 1: Male 44.51877
## 2: Female 30.35422Cette estimation indique un taux d’admission de 44% pour les hommes et de 30% pour les femmes. La différence entre les deux taux d’admission est donc de -14 points de pourcentage. Interprétée comme un effet causal, c’est-à-dire en assimilant le sexe des candidats au résultat d’une expérience aléatoire contrôlée13, cette différence signifierait que 14% des dossiers de candidature envoyés par des hommes n’auraient pas été retenus s’ils avaient été envoyés par des femmes, et conduirait à conclure à l’existence de décisions discriminatoires relativement fréquentes de la part des jurys d’admission.
L’hypothèse centrale de cette comparaison est pourtant très critiquable : en effet, si le sexe des candidats, tel qu’il renseigné dans les candidatures, pouvait être assimilé à une expérience aléatoire contrôlée au niveau de l’université, alors la distribution des départements auxquels sont adressés les dossiers des femmes devrait être la même que celle des départements auxquels sont adressés les dossiers des hommes. Ce n’est pas le cas : Bickel, Hammel et O’Connell (1975) montrent ainsi que (i) femmes et hommes ne postulent pas aux mêmes départements et (ii) les femmes sont plus nombreuses à postuler à des départements dans lequel la sélectivité, mesurée par la part de candidatures rejetées, est plus élevée.
Cela conduit à se demander comment la sélectivité du jury d’admission varie selon le sexe lorsque l’on compare femmes et hommes qui candidatent au même département. En l’espèce, les auteurs montrent que lorsque l’on fait cette comparaison département par département, la part de candidatures rejetées parmi les femmes est en général très proche de celle mesurée parmi les hommes, et que les différences les plus marquées seraient plutôt en faveur des femmes.
Ainsi, lorsque l’on interprète de façon causale ces différences mesurées département par département, c’est-à-dire en supposant que pour chaque département considéré séparément, le sexe déclaré pour chaque candidature est assimilable au résultat d’une expérience aléatoire contrôlée, alors on est conduit à conclure que les pratiques sexistes discriminatoires lors de la phase d’admission sont vraisemblablement peu fréquentes, ou au détriment des hommes.
library(ggplot2)
#On va étudier les décisions d'admission prises par les départements en
# les distinguant les uns des autres
sexbias_dat_dpt<-sexbias_dat[,
list(part_femmes=sum(as.numeric(Gender=="Female")*
N)/
sum(N),
selectivite_hommes=
sum(as.numeric(Admit=="Rejected")*
as.numeric(Gender=="Male")*
N)/
sum(as.numeric(Gender=="Male")*
N),
selectivite_femmes=
sum(as.numeric(Admit=="Rejected")*
as.numeric(Gender=="Female")*
N)/
sum(as.numeric(Gender=="Female")*
N),
taille=sum(N)),
by=Dept]
#Pour mieux visualiser
#Eléments communs aux deux figures
base_fig<-ggplot(data=sexbias_dat_dpt,
aes(x=selectivite_hommes,
size=taille))+
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(ylim=c(0,1),
xlim=c(0,1.05))+#choix d'échelle des axes
scale_y_continuous(labels = scales::percent)+
scale_x_continuous(labels = scales::percent,
breaks=c(0,0.5,1))+
xlab("Candidatures rejetées\n parmi les hommes")+
scale_size(range=c(3,15)
)+
theme(text=element_text(size=32),#taille du texte
strip.text.x = element_text(size=32),
legend.position="none",
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))
#On représente la part de femmes parmi les candidats selon la sélectivité du
# département mesurée par la part de candidatures rejetées parmi les
# candidatures adressées par des hommes à ce département
base_fig+
geom_point(aes(y=part_femmes),
alpha=0.5)+
ylab("\nPart de femmes parmi les candidats")#titre des axes
#On représente la sélectivité à l'égard des femmes en fonction de la sélectivité
# à l'égard des hommes, en comparant à la situation fictive où elles seraient
# exactement la même
base_fig+
geom_point(aes(y=selectivite_femmes),
alpha=0.5)+
geom_line(aes(y=selectivite_hommes),
size=1,
linetype="dashed")+
ylab("Candidatures rejetées\n parmi les femmes")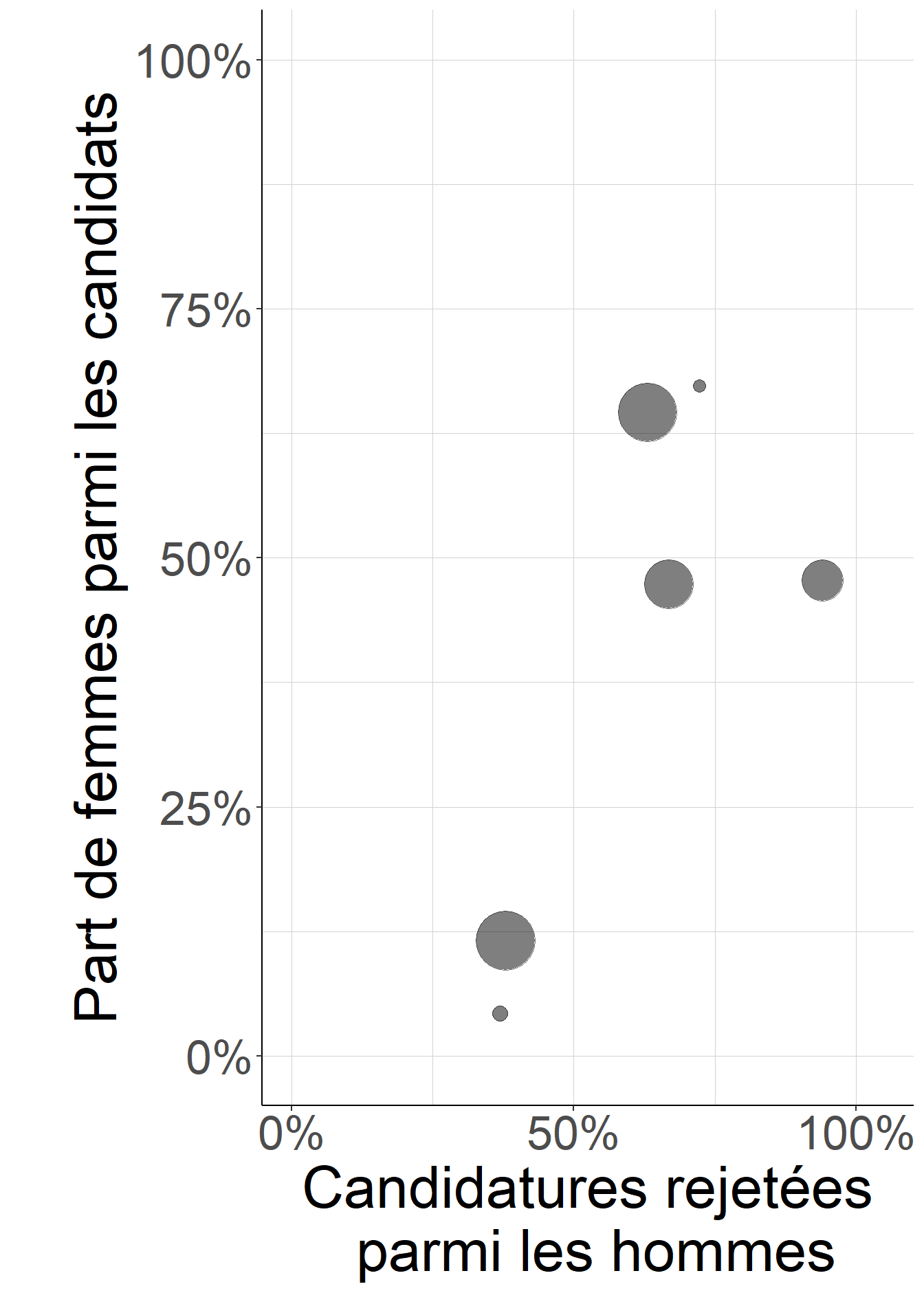
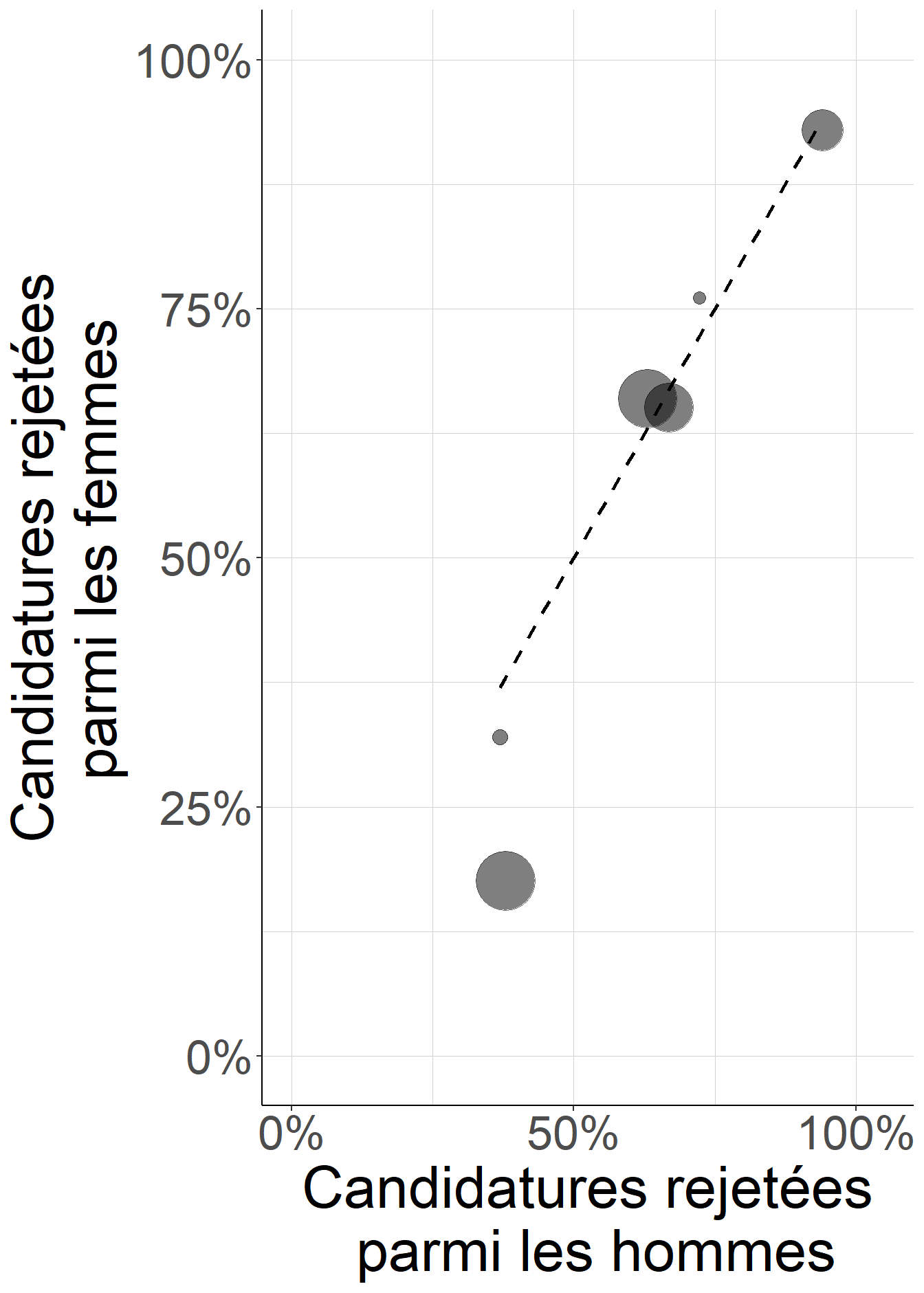
Figure 4.1: Les femmes sont plus nombreuses à candidater dans les départements où la sélectivité mesurée chez les hommes est la plus forte. Lorsque l’on considère les départements séparément les uns des autres, la différence entre la sélectivité vis-à-vis des femmes et la sélectivité vis-à-vis des hommes n’est en général pas flagrante ; lorsqu’elle existe, elle serait plutôt en faveur des femmes qui ont une moindre part de candidatures rejetées (la ligne pointillée représentant la situation d’égalité parfaite).
Ce qui compte ici est le sexe des candidats tel qu’il est perçu par le jury de sorte qu’on peut bien imaginer une expérience hypothétique qui permettrait de le manipuler : cela revient à recourir à la méthodologie des études de correspondance et d’audit. La lectrice ou le lecteur intéressé pourra se référer à cet égard à Bertrand et Mullainathan (2004) pour un exemple sur les catégories raciales aux États-Unis, et Bertrand et Duflo (2017) pour une revue de l’usage de ces techniques.↩︎