2.3 Pourquoi le nom de “moindres carrés ordinaires” ?
Régresser grâce aux moindres carrés ordinaires le salaire horaire (en $ par heure) sur l’éducation (en années passées dans le système scolaire) dans la population des salariés étatstuniens, c’est rechercher un jeu de coefficients \(\alpha\) et \(\beta\) de sorte que la différence entre la valeur du salaire prédite à partir de l’éducation \(\hat{Y}=\alpha + X\beta\) et sa valeur observée \(Y\) soit (i) nulle en moyenne dans la population et (ii) non-corrélée à l’éducation.
Le terme résiduel, c’est-à-dire la différence entre le salaire prédit et le salaire observé, est nul en moyenne ; on peut s’intéresser à sa variance. La variance de ce terme permet en un sens de quantifier combien ce terme est proche de 0, son espérance : plus cette variance est faible, plus rares seront les individus de la population d’intérêt pour lesquels la différence entre salaire prédit et salaire observé dépasse un certain seuil8.
En fait, parmi toutes les façons de construire un salaire prédit comme une fonction affine de l’éducation, la régression linéaire fondée sur la méthode des moindres carrés ordinaires est (i) celle pour laquelle le terme résiduel est de moyenne nulle et de variance minimale dans la population, ou encore, de façon équivalente (ii) celle pour laquelle le carré du terme résiduel est en moyenne le plus faible. Pour le dire autrement, c’est la façon de construire un salaire prédit comme fonction affine de l’éducation telle que ce salaire prédit soit en un sens particulier le plus proche possible du salaire observé quand on se place à l’échelle de la population.
Le fragment de code suivant illustre ce résultat à partir des données du CPS. Il permet de comparer les valeurs de la quantité \(\mathbb{E}[(Y - \hat{Y})^2]\), où \(Y\) correspond au salaire horaire observé et \(\hat{Y}=\alpha + X\beta\) au salaire prédit comme fonction affine de l’éducation lorsque l’on fait varier les valeurs des paramètres \(\alpha\) et \(\beta\). En d’autres termes, il s’intéresse à la moyenne du carré du terme résiduel pour un très grand nombre de façon de prédire le salaire comme fonction affine de l’éducation
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
library(viridis,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On estime la régression du salaire horaire sur l'éducation
reg_wage_educ<-lm(wage~education,
data=CPS)
reg_wage_educ##
## Call:
## lm(formula = wage ~ education, data = CPS)
##
## Coefficients:
## (Intercept) education
## -0.7460 0.7505#On crée une fonction qui pour tout jeu de réels a et b calcul la moyenne du
# carré de l'écart entre le salaire horaire et a+b*education
ecart_carre<-function(a,b){
mean((CPS$wage-a-b*CPS$education)^2)
}
#On la fait tourner sur une grille de valeurs possibles de a et b autour de la
# valeur estimée de coefficients de régression
grille_intercept<-reg_wage_educ$coefficients["(Intercept)"]+
sqrt(vcov(reg_wage_educ)["(Intercept)",
"(Intercept)"])*
1.96/100*
(-100:100)
grille_pente<-reg_wage_educ$coefficients["education"]+
sqrt(vcov(reg_wage_educ)["education",
"education"])*
1.96/100*
(-100:100)
ecart_carre_estime<-rbindlist(lapply(grille_intercept,
function(x){
data.table(
cbind(rep(x,length(grille_pente)),
grille_pente,sapply(
grille_pente,
function(y){
ecart_carre(x,y)
})))
}))
colnames(ecart_carre_estime)[1]<-"grille_intercept"
colnames(ecart_carre_estime)[3]<-"ecartcarre"
#Visualisation
ggplot(data=ecart_carre_estime,
aes(x=grille_intercept,
y=grille_pente,
z=sqrt(ecartcarre)))+
geom_contour(bins=150,
aes(colour = after_stat(level)))+
scale_color_viridis(option="magma",
name="Racine carrée de la moyenne
\ndu carré de l'écart entre le
\nsalaire prédit et le salaire
\nobservé ($ par heure)")+
theme_classic()+#supprime l'arrière-plan gris par défaut
ylab("Coefficient de l'éducation dans le modèle")+#titre des axes
xlab("Intercept dans le modèle")+
geom_hline(yintercept=reg_wage_educ$coefficients["education"],
color="red")+
geom_vline(xintercept=reg_wage_educ$coefficients["(Intercept)"],
color="red")+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
legend.title = element_text(size=12),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))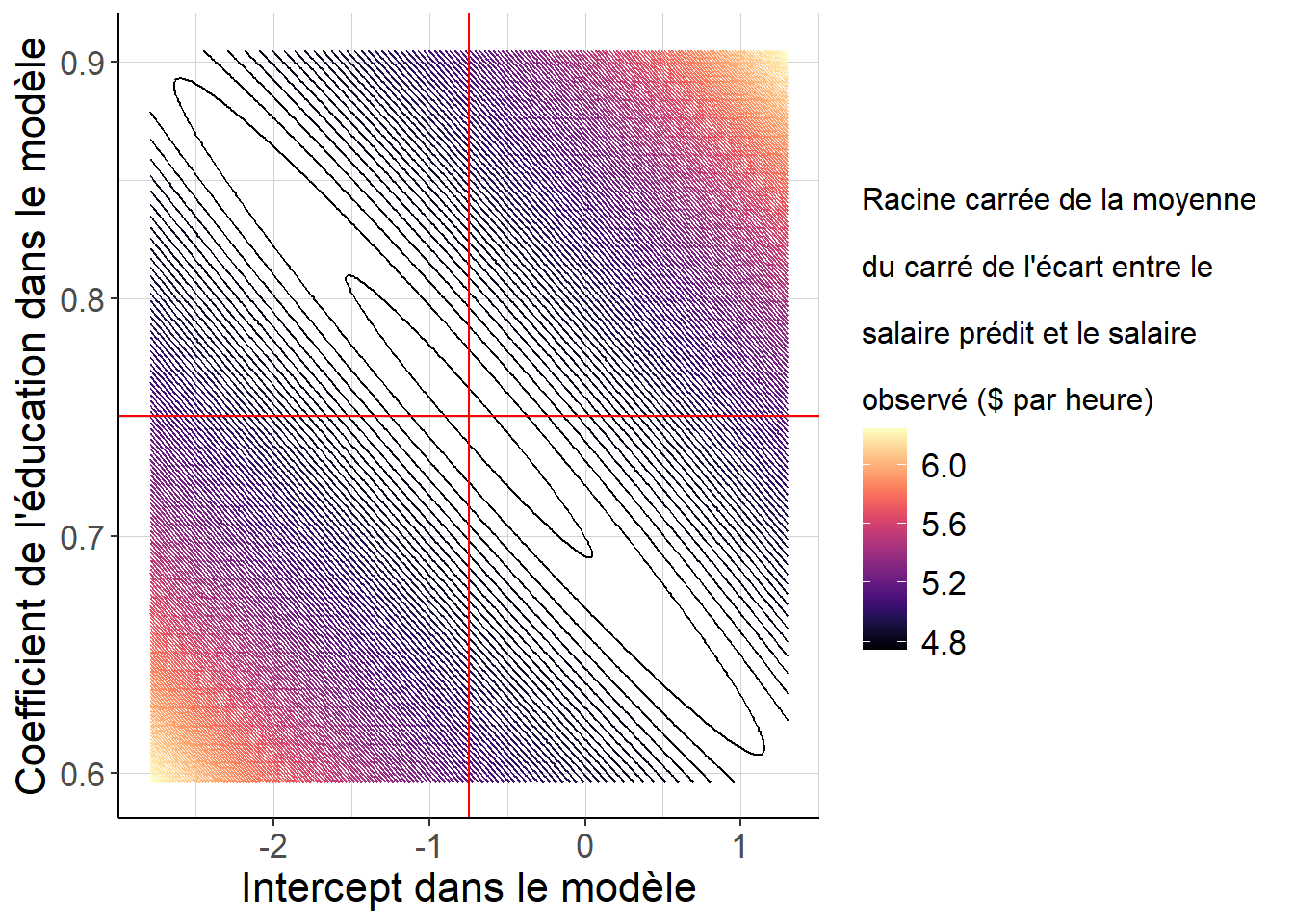
Figure 2.2: Les lignes de niveau de la moyenne du carré de l’écart entre le salaire prédit et le salaire réalisé, lorsque l’on fait varier l’intercept et la pente du modèle, sont des ellipses centrées autour du couple de coefficients renvoyés par la méthode des moindres carrés ordinaires, représenté par l’intersection des deux lignes rouges. La valeur de la moyenne du carré de l’écart entre salaire prédit et salaire réalisé est minimale en ce point précis.
À retenir
Le problème initial consistant à décomposer une variable aléatoire \(Y\) en la somme d’une fonction affine d’une autre variable aléatoire \(X\) et d’un terme d’espérance nulle et non-corrélé avec \(X\) est équivalent au problème consistant à décomposer \(Y\) en la somme d’une fonction affine de \(X\) et un terme d’espérance nulle et de variance minimale, ou encore de façon équivalente un terme dont l’espérance du carré soit aussi faible que possible.
Formellement, la proposition précédente affirme que chercher un réel \(\alpha\), un vecteur \(\beta\) et une variable aléatoire \(\epsilon\) tels que : \[\left\{\begin{array}{l} Y = \alpha + X' \beta + \epsilon \\ \mathbb{E}[\epsilon] = 0 \\ \mbox{Pour tout }i \mbox{ dans }\{1, \dots, d\},\;\mathcal{C}(X_i,\epsilon)=0 \end{array}\right.\] est équivalent au problème consistant à déterminer un réel \(\alpha\) et un vecteur \(\beta\) tels que \(\mathbb{E}[(Y - \alpha- X'\beta)^2]\) soit aussi petit que possible. En d’autres termes, le problème étudié revient à choisir le réel \(\alpha\) et le vecteur \(\beta\) de sorte que la variable \(\hat{Y}=\alpha + X'\beta\) soit en un sens aussi proche que possible de \(Y\), ou de façon équivalente que l’écart entre ces deux variables soit aussi proche que possible de 0, au sens d’une distance qui est l’analogue de la distance euclidienne et qui fait intervenir l’espérance du carré de cet écart.
La lectrice ou le lecteur désireux de pousser plus loin son investigation trouvera une démonstration de ce fait à l’Annexe A.4.