2.7 Agréger les coefficients entre plusieurs groupes
Supposons que l’on régresse, dans la population des salariés étatsuniens, le salaire horaire sur (i) l’éducation mesurée en années passées dans le système scolaire et (ii) une variable dichotomique indiquant que le salarié vit dans un Etat du Sud. Existe-t-il un rapport entre le coefficient sur la variable d’éducation obtenue par cette régression, et ceux que l’on obtiendrait en considérant séparément les salariés qui vivent dans un Etat du Nord d’une part, et ceux qui vivent dans un Etat du Sud d’autre part ?
La réponse à cette question est positive. Il est possible de montrer que lorsque l’on effectue la première régression, le coefficient qui porte sur la variable d’éducation est égal à une moyenne pondérée des coefficients issus des deux régressions distinctes du salaire horaire sur le niveau d’éducation, spécifiques aux Etats du Nord ou du Sud, avec des poids qui donnent davantage d’importance à (i) la région dans laquelle vivent le plus de salariés et (ii) celle où la dispersion du niveau d’éducation entre salariés est la plus prononcée.
Les coefficients de la régression du salaire horaire sur le niveau d’éducation pour les salariés vivant dans un Etat du Nord (respectivement du Sud) s’obtient en comparant deux à deux tous les couples possibles de salariés de ces Etats (voir 2.4). Cela implique donc que lorsque l’on considère sur l’ensemble des salariés étatsuniens, la régression du salaire horaire sur l’éducation et une indicatrice de région, le coefficient portant sur la variable d’éducation (i) résulte de multiples comparaisons de salariés de la même région dont le niveau d’éducation diffère mais (ii) exclut toutes les comparaisons entre salariés vivant dans des régions différentes.
Le fragment de code suivant permet de mettre en évidence ce résultat sur les données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
library(viridis,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On régresse le salaire sur l'éducation et l'indicatrice de région
reg_full_spec<-lm(wage~education + region,
data=CPS)
reg_full_spec##
## Call:
## lm(formula = wage ~ education + region, data = CPS)
##
## Coefficients:
## (Intercept) education regionother
## -1.1394 0.7259 1.0078#On régresse le salaire sur l'éducation dans chaque groupe défini par la région
# et on récupère le coefficient correspondant
reg_educ_region<-lapply(levels(CPS$region),
function(x){
lm(wage~education,
data=CPS[region==x])$coefficients["education"]
})
reg_educ_region<-data.table(reg_educ_region)
reg_educ_region$region<-levels(CPS$region)
#On agrège les coefficients sur l'éducation avec des poids proportionnels à
# 1.la part des effectifs dans chaque région
# 2.la variance de l'éducation dans chaque région
CPS_region<-CPS[,
list(taille_region=.N,
variance=var(education)*
#Attention ici il faut corriger car le dénominateur
# utilisé pour le calcul de la variance est n-1
(sum(as.numeric(wage>=0))-1)/
sum(as.numeric(wage>=0))),
by="region"]
CPS_region<-merge(CPS_region,
reg_educ_region,
by="region")
aggreg_coefficient<-CPS_region[,
list(aggreg_coefficient=
sum(taille_region*
variance*
as.numeric(reg_educ_region))/
sum(taille_region*
variance))]
aggreg_coefficient## aggreg_coefficient
## 1: 0.7258807#On compare les deux coefficients
all.equal(as.numeric(aggreg_coefficient$aggreg_coefficient),
as.numeric(reg_full_spec$coefficients["education"]))## [1] TRUE#Visualisation
#On rajoute juste un peu de bruit à la variable d'éducation pour faciliter la
# visualisation quand il y a plusieurs salariés avec le même niveau
# d'éducation
CPS$jitter_education<-
CPS$education+
(table(CPS$education)[as.character(CPS$education)]>1)*
rnorm(nrow(CPS),sd=0.3)
#Il faut aussi récupérer l'intercept
reg_intercept_region<-lapply(levels(CPS$region),
function(x){
lm(wage~education,
data=CPS[region==x])$coefficients["(Intercept)"]
})
reg_intercept_region<-data.table(reg_intercept_region)
reg_intercept_region$region<-levels(CPS$region)
#Fond commun aux deux panneaux : le nuage de points
nuage<-ggplot(data=CPS,
aes(x=education,
y=wage,
color=region))+
geom_point(alpha=0.3,
aes(x=jitter_education),
linewidth=5)+#génère le nuage de points
scale_color_viridis(discrete = TRUE,
option="magma",
begin=0.2,
end=0.8,
name="Région")+#échelle des couleurs
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(ylim=c(-5,30))+#choix de l'échelle
ylab("Salaire horaire ($ par heure)")+#titre des axes
xlab("Années d'éducation")+
theme(text=element_text(size=32),#taille du texte
strip.text.x = element_text(size=32),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))## Warning in geom_point(alpha = 0.3, aes(x = jitter_education), linewidth = 5):
## Ignoring unknown parameters: `linewidth`#Superposition du nuage de points et des droites issues des régressions séparées
# pour chaque région
nuage+
#droite de régression pour la région south
geom_line(color=viridis_pal(option = "magma",
begin=0.2,
end=0.2)(1),
linewidth=3,
aes(x=jitter_education,
y=as.numeric(reg_intercept_region[region=="south"]$
reg_intercept_region)+
as.numeric(reg_educ_region[region=="south"]$
reg_educ_region)*
jitter_education))+
#droite de régression pour la région other
geom_line(color=viridis_pal(option = "magma",
begin=0.8,
end=0.8)(1),
linewidth=3,
aes(x=jitter_education,
y=as.numeric(reg_intercept_region[region=="other"]$
reg_intercept_region)+
as.numeric(reg_educ_region[region=="other"]$
reg_educ_region)*
jitter_education))
#Superposition du nuage de points et des droites de même pente issue de la
# régression jointe du salaire sur l'éducation et les indicatrices de région
nuage+
#droite de régression pour la région south
geom_line(color=viridis_pal(option = "magma",
begin=0.2,
end=0.2)(1),
linewidth=3,
data=CPS[region=="south"],
aes(x=jitter_education,
y=reg_full_spec$coefficients["(Intercept)"]+
reg_full_spec$coefficients["education"]*jitter_education))+
#droite de régression pour la région other
geom_line(color=viridis_pal(option = "magma",
begin=0.8,
end=0.8)(1),
linewidth=3,
data=CPS[region=="other"],
aes(x=jitter_education,
y=reg_full_spec$coefficients["(Intercept)"]+
reg_full_spec$coefficients["regionother"]*
as.numeric(region=="other")+
reg_full_spec$coefficients["education"]*
jitter_education))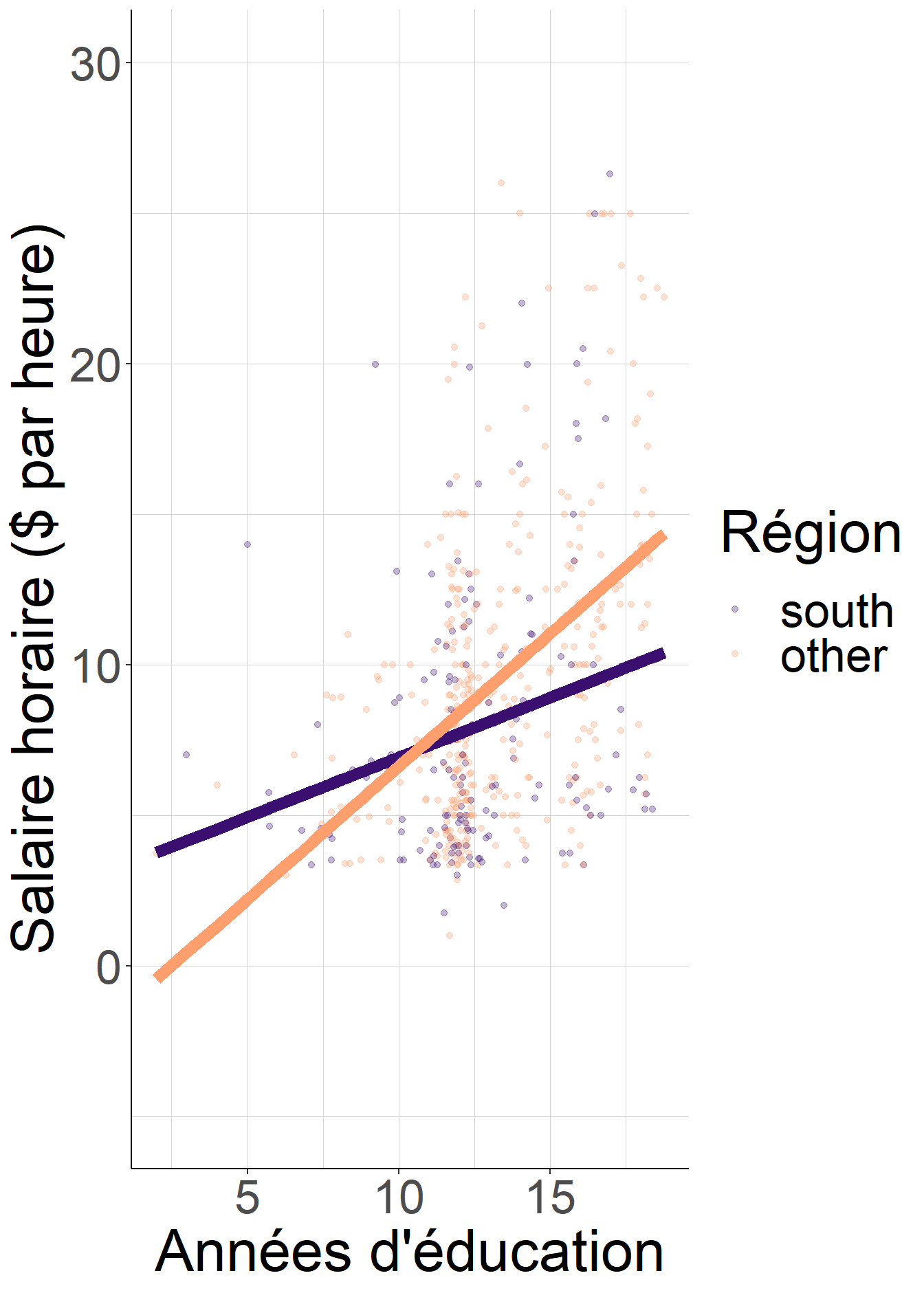
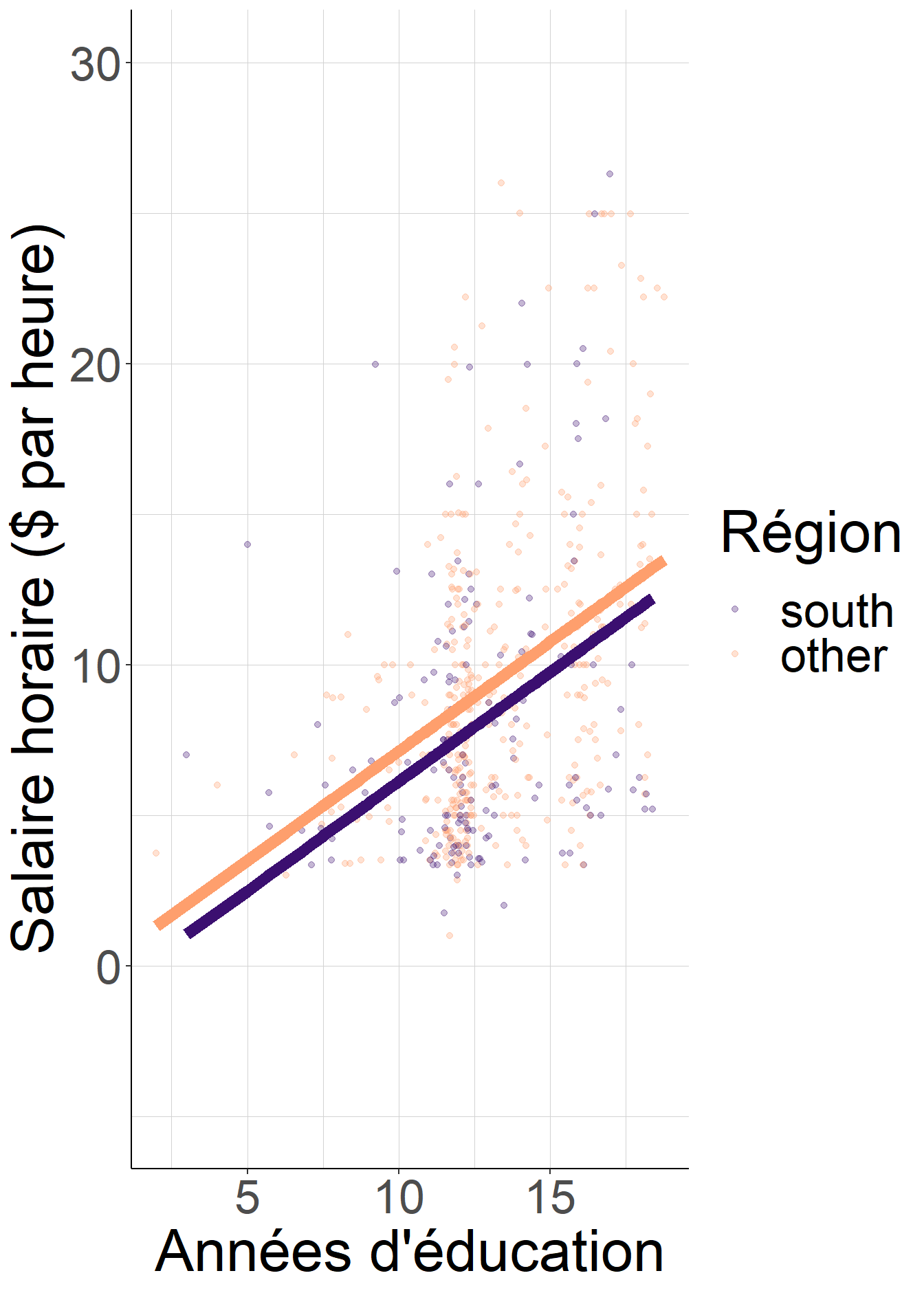
Figure 2.7: Les pentes des droites de régression sont différentes lorsque l’on considère chaque région séparément. Lorsque l’on impose que la pente soit la même quelle que soit la région, en régressant le salaire sur l’éducation et les indicatrices de région, la nouvelle pente commune est égale à une moyenne pondérée des pentes spécifiques à chaque région.
Ce résultat a bien entendu une portée plus générale que ce seul exemple.
À retenir
Lorsque l’on régresse par les moindre carrés ordinaires une variable aléatoire \(Y\) sur (i) une variable quelconque \(X\) et (ii) un lot de variables dichotomiques \(D_i\) qui découpent l’ensemble des résultats possibles en autant de sous-ensembles disjoints, le coefficient sur la variable \(X\) est égal à la moyenne des coefficients que l’on obtient en régressant \(Y\) sur \(X\) à l’intérieur de chacun des groupes définis par \(X_i=1\), avec des poids qui donnent davantage d’importance (i) aux groupes les plus nombreux dans la population d’intérêt et (ii) aux groupes au sein desquels la variance conditionnelle de \(X\) est plus grande.
La preuve de ce résultat est développée en Annexe A.10.