B.5 Approche à la Oaxaca-Blinder pour estimer les effets causaux moyens d’une intervention
La décomposition d’Oaxaca-Blinder (Oaxaca (1973); Blinder (1973)) est un outil couramment utilisé pour décomposer les disparités entre groupes sur le marché du travail, et notamment les écarts de salaire entre femmes et hommes, ou entre catégories ethno-raciales aux États-Unis. Schématiquement, le principe en est de régresser dans une première étape le salaire sur les caractéristiques productives, c’est-à-dire les caractéristiques observables importantes pour la fixation du salaire, séparément pour les femmes et pour les hommes, puis d’utiliser les coefficients estimés chez les femmes pour imputer aux hommes, sur la base de leurs caractéristiques productives, ce qu’aurait été leur salaire s’ils avaient été des femmes. Quelques manipulations algébriques faciles permettent de montrer que l’écart de salaire moyen entre femmes et hommes peut alors s’écrire comme la somme de la différence entre le salaire moyen observé des hommes et leur salaire moyen imputé, ce que l’on appelle souvent la part inexpliquée, et la différence entre le salaire moyen imputé des hommes et le salaire moyen observé des femmes, ce que l’on appelle la part expliquée et qui quantifie en un sens la contribution des différences moyennes de caractéristiques productives entre femmes et hommes à l’écart de salaire moyen.
On peut transposer avec quelques adaptations cette idée simple à l’exemple de l’expérience aléatoire contrôlée défectueuse de Gerber et Green (2000) réanalysée par Imai (2005), en supposant donc valables les hypothèses d’indépendance conditionnelle et de support commun que l’on a fait pour toutes les approches précédentes. L’approche proposée ici est une adaptation avec quelques différences d’une procédure proposée par Kline (2011). La marche à suivre est :
- on régresse le taux de participation électorale sur les variables de conditionnement séparément pour les individus qui ont reçu l’appel téléphonique incitant à voter et pour ceux qui ne l’ont pas reçu ;
- on utilise ces coefficients pour imputer à chaque individu, qu’il ait ou qu’il n’ai pas reçu l’appel téléphonique, les deux valeurs prédites par les deux régressions linéaires précédentes ;
- on calcule pour toute la population de New Haven la moyenne de la différence entre ces deux valeurs prédites.
On peut montrer que cette approche est équivalente à une approche par repondération, à la différence – potentiellement importante – près que les poids utilisés ne sont pas l’inverse (des valeurs estimées) du score de propension, mais les valeurs prédites des poids fondés sur les vraies valeurs, inconnues, du score de propension par une régression linéaire infaisable de ces poids sur les variables de conditionnement. Ainsi, la quantité estimée par la différence moyenne entre les valeurs prédites par les deux régressions coïncide avec les effets causaux moyens de l’appel téléphonique sur la participation électorale :
- si, dans chacun des deux groupes définis par le fait d’avoir reçu ou non l’appel téléphonique, les valeurs des poids, prédites par une régression linéaire, et les vraies valeurs des poids coïncident, ou ;
- si, dans chacun des deux groupes définis par le fait d’avoir reçu ou non l’appel téléphonique, le taux de participation électorale dans chaque strate définie par la valeur des variables de conditionnement coïncide avec le taux de participation électorale estimé par une régression linéaire.
La lectrice ou le lecteur intéressé par un développement plus formel sur ce résultat le trouvera en Annexe A.17.
Parce que ce résultat fait référence non pas au score de propension en lui-même, mais aux valeurs prédites par une régression linéaire des poids calculés à partir des vraies valeurs du score de propension sur les variables de conditionnement, il peut sembler difficile à utiliser. En fait, il est possible de calculer ces pseudo-poids à partir des données, et donc d’en inférer (parce que les poids sont définis à un facteur multiplicatif près comme l’inverse du (complément du ) score propension) les valeurs estimées du score de propension qu’utiliserait une approche par repondération qui donnerait exactement les mêmes résultats. Une fois que l’on a calculé ces valeurs estimées du score de propension, on peut revenir au travail que l’on fait ordinairement pour les approches fondées sur le score de propension, c’est-à-dire évaluer la crédibilité de l’hypothèse de support commun, et mettre à l’épreuve la propriété équilibrante du score de propension.
Le fragment de code suivante effectue ce travail sur l’exemple de Gerber et Green (2000) et Imai (2005).
library(data.table)
library(ggplot2)
library(Matching)
#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)[WARD!="22"]
#pour éliminer le problème de support commun
#On veut connaître le score de propension sur lequel est implicitement
# fondé cette approche
#Pour cela, il faut commencer par estimer les pseudo-poids
#Le plus pratique pour cela est de récupérer les matrices qui servent à
# l'estimation des régressions linéaires
#On va donc commencer par estimer ces régressions
reg_imai_appel<-
lm(VOTED98 ~
PERSONS +
WARD +
AGE +
MAJORPTY +
VOTE96.0 +
VOTE96.1 +
AGE2 +
PERSONS*VOTE96.0 +
PERSONS*NEW -
NEW,
data=GerberGreenImai[PHN.C1==1],
x=TRUE)
reg_imai_sans_appel<-
lm(VOTED98 ~
PERSONS +
WARD +
AGE +
MAJORPTY +
VOTE96.0 +
VOTE96.1 +
AGE2 +
PERSONS*VOTE96.0 +
PERSONS*NEW -
NEW,
data=GerberGreenImai[PHN.C1==0],
x=TRUE)
#Ce dont on a en particulier besoin : l'inverse de X'X
termeXprimeX_appel<-
nrow(GerberGreenImai[PHN.C1==1])*
solve(t(reg_imai_appel$x)%*%(reg_imai_appel$x))
termeXprimeX_sans_appel<-
nrow(GerberGreenImai[PHN.C1==0])*
solve(t(reg_imai_sans_appel$x)%*%(reg_imai_sans_appel$x))
#On a aussi besoin d'un terme qui estime la moyenne de chaque variable
# des régressions linéaires, non pas dans les groupes séparément mais
# dans toute la population de New Haven
#Le plus simple pour ça
matrice_population<-
lm(VOTED98 ~
PERSONS +
WARD +
AGE +
MAJORPTY +
VOTE96.0 +
VOTE96.1 +
AGE2 +
PERSONS*VOTE96.0 +
PERSONS*NEW -
NEW,
data=GerberGreenImai,
x=TRUE)$x
moyenne_population<-
1/nrow(GerberGreenImai)*
colSums(matrice_population)
#Une fois qu'on a ça on peut calculer le vecteur de coefficients qui permet
# de construire les poids à partir des covariables
coeff_poids_appel<-
termeXprimeX_appel%*%as.matrix(moyenne_population)
coeff_poids_sans_appel<-
termeXprimeX_sans_appel%*%as.matrix(moyenne_population)
#Et on peut finalement construire les poids eux-mêmes
poids_appel<-reg_imai_appel$x%*%coeff_poids_appel
poids_sans_appel<-reg_imai_sans_appel$x%*%coeff_poids_sans_appel
#On remet ça dans la table de départ
GerberGreenImai$poids_oaxaca_blinder<-rep(NA_real_,nrow(GerberGreenImai))
GerberGreenImai[PHN.C1==1]$poids_oaxaca_blinder<-poids_appel
GerberGreenImai[PHN.C1==0]$poids_oaxaca_blinder<-poids_sans_appel
#Et on calcule finalement le score de propension implicite
GerberGreenImai[,
pscore_oaxaca_blinder:=
fcase(
PHN.C1==1,
mean(GerberGreenImai$PHN.C1)/
poids_oaxaca_blinder,
PHN.C1==0,
(poids_oaxaca_blinder-
1+
mean(GerberGreenImai$PHN.C1))/
poids_oaxaca_blinder
)]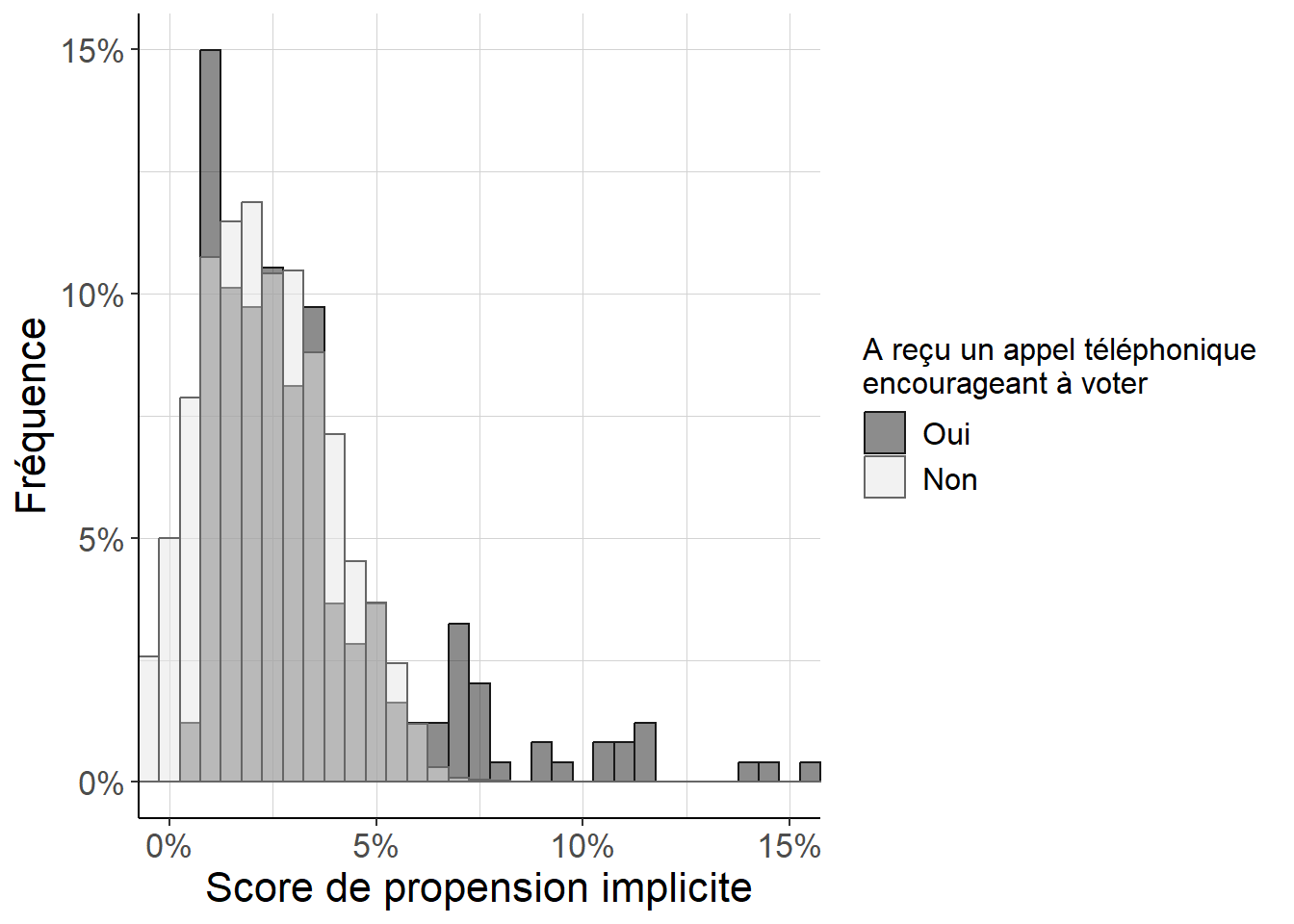
Figure B.2: Histogramme répliquant Imai (2005) (figure 8) pour examiner la distribution des scores de propension implicites dans l’estimation à la Oaxaca-Blinder. Parce que l’on est, en dépit de ses défauts, dans un cas proche d’une expérience aléatoire contrôlée avec une faible probabilité de recevoir un appel téléphonique appelant à voter, on peut voir que (i) les scores de propension sont faibles pour tous les individus, et (ii) les différences entre individus ayant reçu ou n’ayant pas reçu d’appel téléphonique restent relativement faibles. Cependant, on voit aussi que le score de propension est également en général plus important pour les individus ayant reçu un appel téléphonique que pour les autres. Un dernier trait potentiellement important ici est que l’on note quelques valeurs négatives du score de propension estimé : cela signale que l’approximation linéaire pour les poids (et non pour le score de propension comme c’est le cas pour l’usage habituel de la régression linéaire) n’est pas parfaite.
Une fois que l’on connaît les poids et le score de propension, il est naturel de mettre à l’épreuve la propriété équilibrante du score de propension. Il y a ici une difficulté par rapport au cas habituel : mécaniquement et indépendamment de la qualité de l’estimation, les poids implicites sont tels que si l’on considère les moyennes des variables incluses dans les régressions, l’écart entre les deux groupes après repondération est strictement égal à 0. Le fragment de code suivant met en évidence ce fait.
#Avec ces poids implicites, on va comparer du point de vue de la valeur
# des variables de conditionnement les individus selon qu'ils ont ou qu'ils
# n'ont pas reçu un appel téléphonique
#Fonction qui renvoie la différence moyenne entre le groupe qui fait
# l'objet de l'intervention et celui qui n'en fait pas l'objet
diff_moy<-function(variable,
groupe_intervention,
poids=NULL){
if(is.null(poids)){
(sum(groupe_intervention*variable)/
sum(groupe_intervention)-
(sum((1-groupe_intervention)*variable))
/sum(1-groupe_intervention))
}
else{
(sum(poids*groupe_intervention*variable)/
sum(poids*groupe_intervention)-
(sum(poids*(1-groupe_intervention)*variable))
/sum(poids*(1-groupe_intervention)))
}
}
#On applique la fonction diff_moy aux variables de conditionnement, d'abord sans
# repondération, puis avec les nouveaux poids
#On définit les variables de conditionnement sur lesquelles on va tester
# la propriété équilibrante du score de propension
variables_conditionnement<-c("PERSONS",
"AGE",
"MAJORPTY",
"VOTE96.0",
"VOTE96.1",
"NEW")
#Sans repondération : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement
contrastes_bruts<-GerberGreenImai[,
lapply(X=.SD,
FUN=function(x){
list(
diff_moy(
variable=x,
groupe_intervention=PHN.C1),
sqrt(0.5*var(x)))
}),
.SDcols=variables_conditionnement]
contrastes_bruts[,
stat:=c("diff_moy",
"spread")]
contrastes_bruts<-melt(contrastes_bruts,
variable.name="variable",
value.name="valeur",
id.vars="stat")
#Avec repondération
contrastes_agreges_reponderation_oaxaca_blinder<-
GerberGreenImai[,
lapply(
X=.SD,
FUN=function(x){
diff_moy(variable=x,
groupe_intervention=
PHN.C1,
poids=poids_oaxaca_blinder)
}),
.SDcols=variables_conditionnement]
contrastes_agreges_reponderation_oaxaca_blinder[,
stat:="diff_moy"]
contrastes_agreges_reponderation_oaxaca_blinder<-
melt(contrastes_agreges_reponderation_oaxaca_blinder,
id.vars="stat",
value.name="valeur",
variable.name="variable")
#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
#On crée une fonction qui fait ça et qui sera utile pour les autres techniques
contrastes_propre<-function(contrastes_bruts_dat,
contrastes_pscore_dat){
contrastes_propre_dat<-rbind(contrastes_bruts_dat,
contrastes_pscore_dat,
idcol="etape")
contrastes_propre_dat<-rbind(contrastes_propre_dat,
contrastes_propre_dat[stat=="spread",
-c("etape")],
fill=TRUE)[is.na(etape),
etape:=2]
contrastes_propre_dat<-
contrastes_propre_dat[,
list(diff_std=
sum(as.numeric(stat=="diff_moy")*
as.numeric(valeur))/
sum(as.numeric(stat=="spread")*
as.numeric(valeur))),
by=c("variable",
"etape")]
}
contrastes_reponderation_oaxaca_blinder<-
contrastes_propre(contrastes_bruts,
contrastes_agreges_reponderation_oaxaca_blinder)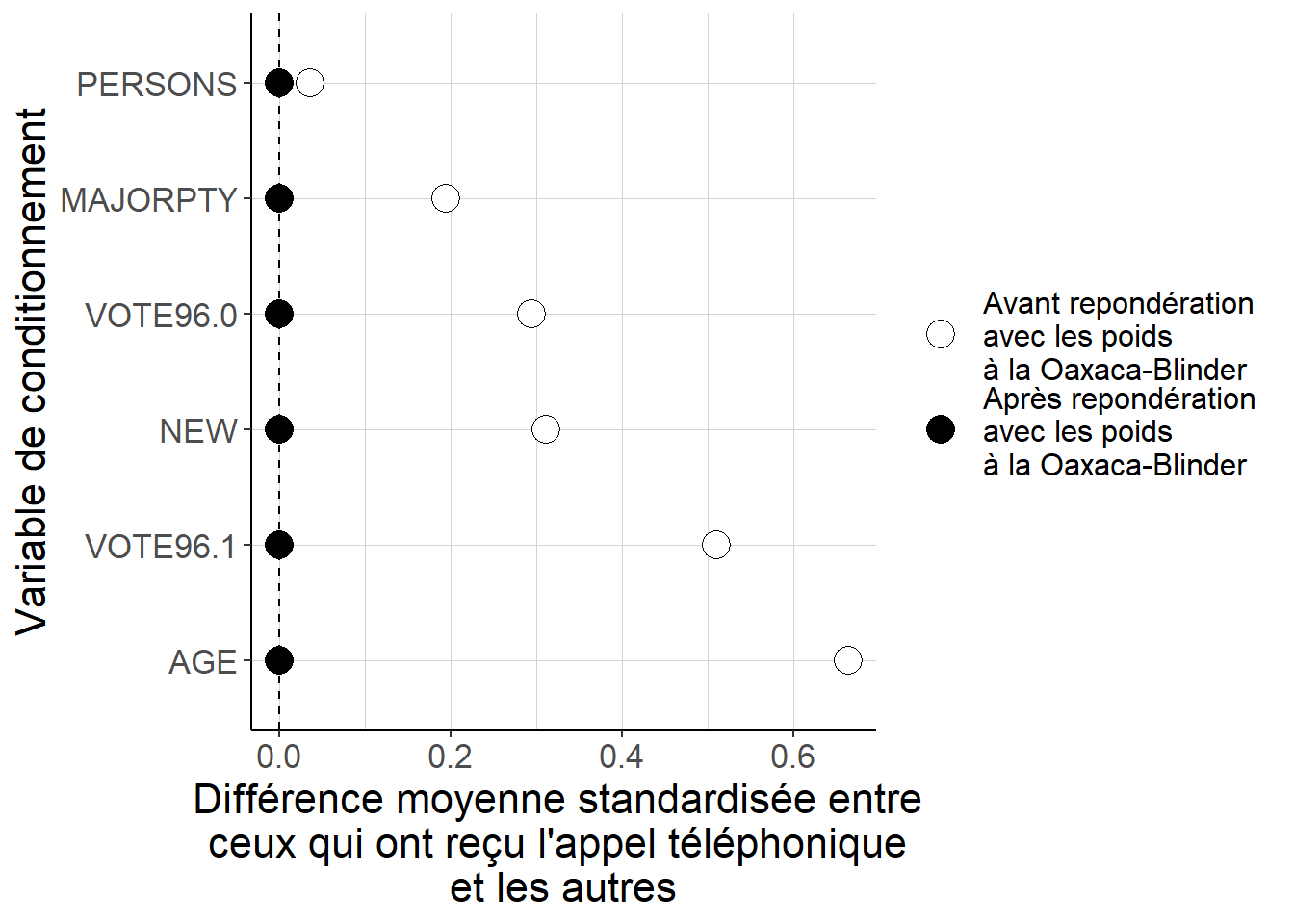
Figure B.3: Mécaniquement et indépendamment de la qualité de l’approximation linéaire pour les poids, les différences moyennes entre les deux groupes après repondération lorsque l’on utilise les poids implicites liés à l’approche à la Oaxaca-Blinder sont identiquement nulles. Il n’est donc pas possible d’utiliser ces différences pour évaluer la qualité de l’estimation.
La propriété équilibrante du score de propension ne concerne pas seulement les moyennes des différentes variables de conditionnement, mais bien toute leur distribution dans chacun des groupes. La solution pour résoudre ce problème est donc ou bien de passer par une stratification, ou bien de se concentrer sur d’autres mesures que les différences de moyennes des variables incluses dans les régressions. Par exemple, on peut choisir de considérer plutôt des écarts de médiane lorsque l’on considère des variables continues ; on peut aussi considérer par exemple le ratio des variances. Pour des variables dichotomiques, le passage par la médiane ou la variance ne sera pas informatif : il faut continuer à regarder des écarts de moyenne, mais on peut imaginer de considérer plutôt des interactions entre variables dichotomiques que l’on a pas incluses dans la régression. Le framgent de code suivant propose de conserver la différence des moyennes, mais de considérer des variables définies de façon non-linéaire à partir de celles incluses dans la régression.
#Avec ces poids implicites, on va comparer du point de vue de la valeur
# des variables de conditionnement les individus selon qu'ils ont ou qu'ils
# n'ont pas reçu un appel téléphonique
#On applique la fonction diff_moy aux variables de conditionnement, d'abord sans
# repondération, puis avec les nouveaux poids
#On définit les variables de conditionnement sur lesquelles on va tester
# la propriété équilibrante du score de propension
#Il faut les définir de façon non-linéaire à partir des variables incluses
# dans les régressions
GerberGreenImai[,
c("AREA*VOTE96.0",
"OLD",
"YOUNG",
"NEW*MAJORPTY",
"NEW*AGE"):=list(
as.numeric(as.numeric(WARD)<15)*VOTE96.0,
as.numeric(AGE>quantile(GerberGreenImai$AGE,
probs=0.75)),
as.numeric(AGE<=quantile(GerberGreenImai$AGE,
probs=0.25)),
NEW*MAJORPTY,
NEW*AGE)]
variables_conditionnement_nonlin<-
c("AREA*VOTE96.0",
"OLD",
"YOUNG",
"NEW*MAJORPTY",
"NEW*AGE")
#Sans repondération : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement
contrastes_bruts_nonlin<-
GerberGreenImai[,
lapply(X=.SD,
FUN=function(x){
list(
diff_moy(
variable=x,
groupe_intervention=PHN.C1),
sqrt(0.5*var(x)))
}),
.SDcols=variables_conditionnement_nonlin]
contrastes_bruts_nonlin[,
stat:=c("diff_moy",
"spread")]
contrastes_bruts_nonlin<-melt(contrastes_bruts_nonlin,
variable.name="variable",
value.name="valeur",
id.vars="stat")
#Avec repondération
contrastes_agreges_reponderation_oaxaca_blinder_nonlin<-
GerberGreenImai[,
lapply(
X=.SD,
FUN=function(x){
diff_moy(variable=x,
groupe_intervention=
PHN.C1,
poids=poids_oaxaca_blinder)
}),
.SDcols=variables_conditionnement_nonlin]
contrastes_agreges_reponderation_oaxaca_blinder_nonlin[,
stat:="diff_moy"]
contrastes_agreges_reponderation_oaxaca_blinder_nonlin<-
melt(contrastes_agreges_reponderation_oaxaca_blinder_nonlin,
id.vars="stat",
value.name="valeur",
variable.name="variable")
#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
contrastes_reponderation_oaxaca_blinder_nonlin<-
contrastes_propre(contrastes_bruts_nonlin,
contrastes_agreges_reponderation_oaxaca_blinder_nonlin)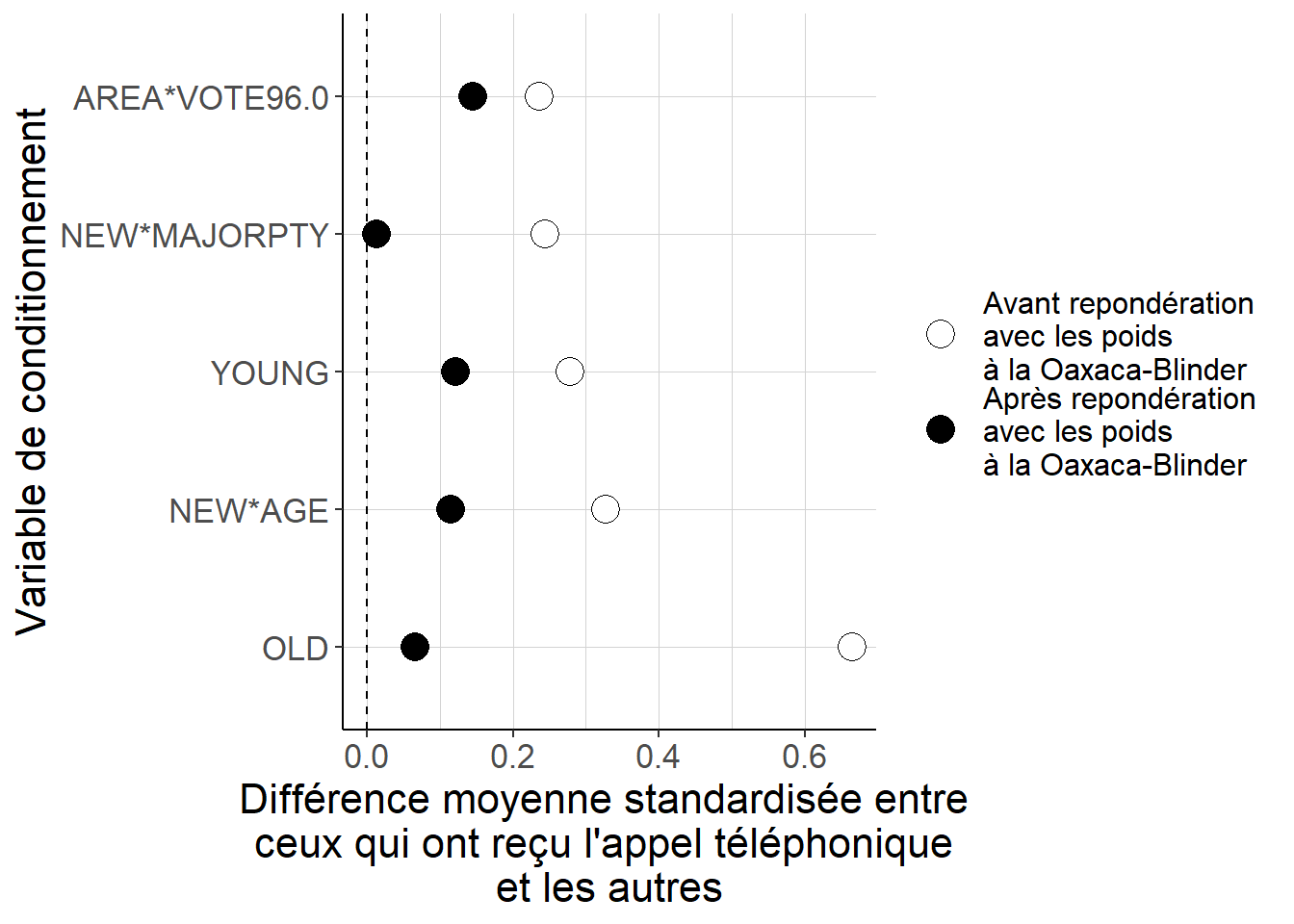
Figure B.4: Lorsque l’on considère des variables définies de façon non-linéaire à partir des variables incluses dans les régressions, on peut voir que les différences de moyenne entre les groupes après repondération avec les poids implicites liés à l’approche à la Oaxaca-Blinder sont plus faibles qu’avant, mais qu’elles ne sont pas mécaniquement égales à 0. En d’autres termes, ces poids permettent vraisemblablement de s’approcher d’un meilleur équilibrage de deux groupes, mais celui-ci n’est pas parfait : l’approximation linéaire des poids n’est pas tout à fait satisfaisante.
Une fois ce travail réalisé, on peut passer à l’estimation proprement dite. On vérifie ici que l’estimation en passant par les valeurs prédites sur l’ensemble de la population des régressions estimées séparément dans chaque groupe donnent bien un résultat semblable à celui que l’on obtient avec la repondération. Ici utiliser les poids normalisés ou non ne change rien : comme la constante est incluse dans les covariables, la moyenne des poids, c’est-à-dire la moyenne de 1 pondérée avec les poids est égale à la moyenne de 1 dans toute la population, c’est-à-dire 1. Le fragment de code suivant réalise ce travail.
#On commence par l'estimation par repondération
#Estimation de l'ATE avec les poids non-normalisés
ATE_reponderation_oaxaca_blinder_nonnorm<-
GerberGreenImai[,
list(ATE=
sum(poids_oaxaca_blinder*PHN.C1*VOTED98)/
sum(PHN.C1)-
sum(poids_oaxaca_blinder*(1-PHN.C1)*VOTED98)/
sum(1-PHN.C1))]
ATE_reponderation_oaxaca_blinder_nonnorm## ATE
## 1: 0.1256683#Estimation de l'ATE avec les poids normalisés
ATE_reponderation_oaxaca_blinder_norm<-
GerberGreenImai[,
list(ATE=
sum(poids_oaxaca_blinder*PHN.C1*VOTED98)/
sum(poids_oaxaca_blinder*PHN.C1)-
sum(poids_oaxaca_blinder*(1-PHN.C1)*VOTED98)/
sum(poids_oaxaca_blinder*(1-PHN.C1)))]
ATE_reponderation_oaxaca_blinder_norm## ATE
## 1: 0.1256683#On vérifie qu'ici la normalisation n'apporte rien
all.equal(
ATE_reponderation_oaxaca_blinder_nonnorm,
ATE_reponderation_oaxaca_blinder_norm)## [1] TRUE#On compare à l'approche avec les valeurs prédites
#Il faut partir de la matrice avec tous les individus en ligne et des
# vecteurs de coefficients récupérés avec les régressions
prediction_appel<-
matrice_population%*%as.matrix(reg_imai_appel$coefficients)
prediction_sans_appel<-
matrice_population%*%as.matrix(reg_imai_sans_appel$coefficients)
ATE_oaxaca_blinder<-
mean(prediction_appel)-
mean(prediction_sans_appel)
ATE_oaxaca_blinder## [1] 0.1256683all.equal(
as.numeric(ATE_reponderation_oaxaca_blinder_nonnorm),
ATE_oaxaca_blinder)## [1] TRUE