2.9 Estimation et inférence
L’estimation d’une régression linéaire à partir de données observées pose des questions très semblables à celles qui se présentent quand on considère l’estimation de l’espérance à partir de la moyenne empirique (voir 1.3.6). On peut considérer le tirage aléatoire d’un échantillon de quelques individus au sein d’une population plus grande. Soit \(n\) un entier naturel non-nul, qui correspond au nombre d’individus tirés, et soient \((X_1, Y_1)\) jusqu’à \((X_n, Y_n)\) des couples de variables aléatoires indépendantes de même loi jointe, les variables aléatoires \(X_1\) à \(X_n\) étant à valeurs dans \(\mathbb{R}^d\) et \(Y_1\) à \(Y_n\) à valeurs dans \(\mathbb{R}\). La variable alatoire \(X_i\) désigne ici la valeur de la variable \(X\) à laquelle on s’intéresse pour le \(i\)-ème tirage d’un individu dans la population, de même que la variable \(Y_i\) désigne la valeur de la variable \(Y\) pour le \(i\)-ème individu tiré. Comme on tire de façon équiprobable dans la population, toutes les variables \(X_i\) doivent avoir la même espérance, qui est essentiellement la moyenne de la variable \(X\) dans la population entière, par opposition à la moyenne dans l’échantillon que l’on vient de tirer. De même la matrice de variance-covariance de la variable aléatoire \(X_i\) ne dépend pas de \(i\) et s’identifie à la matrice de variance-covariance de \(X\) prise dans toute la population. La même remarque vaut pour les variables \(Y_i\). En fait, de façon générale, pour toute fonction \(\phi\) on peut considérer sans ambiguïté la quantité \(\mathbb{E}[\phi(X, Y)]\), c’est-à-dire la moyenne de \(\phi(X, Y)\) dans toute la population, et l’espérance \(\mathbb{E}[\phi(X_i, Y_i)]\) est égale à cette moyenne pour chaque tirage \(i\) considéré.
Remarque
Tout ce qui suit par du principe que le problème posé par l’inférence est celui du passage de quantités estimées dans un petit échantillon à des quantités définies à l’échelle d’une grande population. Cette approche n’est pas toujours très convaincante, en particulier lorsque l’on utilise des données exhaustives. Des auteurs importants recommandents de s’appuyer sur des approches un peu différentes de l’incertitude, qui s’apparentent beaucoup à celles qui sont souvent employées lorsque l’on étudie les résultats d’expériences aléatoires contrôlées (Abadie et al. (2020)).
2.9.1 Représentation matricielle
À partir de ces \(n\) tirages, on peut former une variable aléatoire à valeurs dans l’espace des matrices de taille \(n \times d\) notée \(\mathbf{X}\) dont la première ligne est la transposée variable aléatoire \(X_1\), la deuxième ligne la transposée de variable aléatoire \(X_2\) et ainsi de suite jusqu’à \(X_n\). Ainsi, la \(i\)-ème ligne \(j\)-ème colonne de \(\mathbf{X}\) correspond à la \(j\)-ème composante de la variable aléatoire \(X_i\), c’est-à-dire à la \(j\)-ème composante du \(i\)-ème tirage dans la population. En d’autres termes, la matrice \(\mathbf{X}\) empile les \(n\) observations qui apparaissent comme autant de lignes qui listent les valeurs des différentes variables indépendantes.
On peut en faire de même pour la variable dépendante en créant une variable aléatoire à valeurs dans l’espace des matrices colonne de taille \(n \times 1\) notée \(\mathbf{Y}\) dans laquelle on stocke les \(n\) tirages de la variable dépendante, dans le même ordre que pour \(\mathbf{X}\). Pour bien distinguer les composantes des tirages, dans tout ce qui suit on notera les composantes en exposants et les tirages en indices. Ainsi, \(X_{i}^{k}\) désigne la \(k\)-ème composante du \(i\)-ème tirage, envisagée comme une variable aléatoire. En définitive : \[\begin{array}{cc} \mathbf{X}:=\left(\begin{array}{ccccc} X_1^1 & X_1^2 & \cdots & X_{1}^{d-1} & X_i^d \\ X_2^1 & X_2^2 & \cdots & X_2^{d-1} & X_2^d \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ X_{n-1}^1 & X_{n-1}^2 & \cdots & X_{n-1}^{d-1} & X_{n-1}^d \\ X_n^1 & X_n^2 & \cdots & X_n^{d-1} & X_n^d \\ \end{array}\right) & n\mbox{ observations}\\ d \mbox{ variables} & \\ \end{array}\]
On peut multiplier à gauche \(\mathbf{X}\) par sa transposée \(\mathbf{X}'\), et le résultat de cette multiplication est une variable aléatoire à valeurs dans l’espace des matrices de taille \(d \times d\). Compte-tenu de la définition du produit matriciel, la \(k\)-ème ligne \(l\)-ème colonne de \(\mathbf{X}'\mathbf{X}\) est égale à la somme sur tous les individus tirés du produit des \(k\)-ème et \(l\)-ème composante des variables indépendantes : \(\sum_{i=1}^n X_i^k X_{i}^l\). Par conséquent, en vertu de la discussion sur le comportement asymptotique de la moyenne empirique, pour \(k\) et \(l\) dans \(\{1,\dots, d\}\), on sait que lorsque \(n\) tend vers l’infini, \(\frac{1}{n}\sum_{i=1}^n X_j^k X_{i}^l\) s’approche de \(\mathbb{E}[X_kX_l]\). En d’autres termes, la variable aléatoire \(\frac{1}{n}\mathbf{X}'\mathbf{X}\) s’identifie dans la limite d’un très grand nombre de tirages à la matrice \(\mathbb{E}[XX']\).
On peut faire de même en multipliant \(\mathbf{Y}\) à gauche \(\mathbf{X}'\), et le résultat de cette multiplication est une variable aléatoire à valeurs dans l’espace des matrices colonnes de taille \(d \times 1\). En revenant à la définition du produit matriciel, la \(k\)-ème ligne de \(\mathbf{X}'\mathbf{Y}\) est égale à la somme sur tous les individus tirés du produit de la \(k\)-ème composante des variables indépendantes par la variable dépendante : \(\sum_{j=1}^n X_{j}^k Y_j\). En suivant ce qui précède, la variable aléatoire \(\frac{1}{n}\mathbf{X}'\mathbf{Y}\) s’identifie dans la limite d’un très grand nombre de tirages à la matrice \(\mathbb{E}[XY]\).
Tous les résultats précédents reposent sur la loi des grands nombres qui dicte le comportement asymptotique de la moyenne empirique. La lectrice ou le lecteur désireux de se remettre en mémoire l’étude asymptotique de la moyenne empirique est invité à se rendre en 1.3.6 et 1.4.3.
2.9.2 Estimateur des moindres carrés ordinaires
On a vu dans ce qui précède que si pour tout \(i\) dans \(\{1, \dots, n\}\) les composantes des variables aléatoires \(X_i\) sont linéairement indépendantes, alors il existe un unique vecteur \(\beta\) de \(\mathbb{R}^d\) et une unique famille de variables aléatoires \(\epsilon_1\) à \(\epsilon_n\) tel que : \[\left\{\begin{array}{c} Y_i = X_i' \beta + \epsilon_i \\ \mathbb{E}[\epsilon_i]=0 \\ \mathbb{E}[X_i \epsilon_i]=0 \end{array} \right.\] De plus, on sait exprimer le vecteur \(\beta\) en fonction des variables aléatoires en question : \(\beta = \mathbb{E}[XX']^{-1}\mathbb{E}[XY]\). La difficulté est bien entendu que ces quantités ne peuvent pas être observées directement dans les données.
Le paragraphe précédent permet toutefois d’approcher ces quantités. En effet, la discussion précédente implique que dans la limite d’un très grand nombre de tirages, \(\frac{1}{n}\mathbf{X}'\mathbf{X}\) s’identifie à la matrice \(\mathbb{E}[XX']\) et \(\frac{1}{n}\mathbf{X}'\mathbf{Y}\) à la matrice \(\mathbb{E}[XY]\).
Définition
Avec les notations précédentes, la variable aléatoire \((\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{Y}\), souvent notée \(\hat{ \beta}\) est appelée l’estimateur des moindres carrés ordinaires.
À retenir
L’estimateur des moindres carrés ordinaires \(\hat{\beta}\) s’identifie lorsque le nombre d’observations tend vers l’infini avec le vecteur \(\beta\).
Ainsi dans le formalisme utilisé \(\beta\) est un vecteur de \(\mathbb{R}^d\) qui ne varie pas, tandis que \(\hat{\beta}\) est une variable aléatoire qui fluctue en fonction du tirage des individus observés dans les données.
Avertissement
Il importe ici encore plus qu’ailleurs de bien faire la distinction entre \(\beta\), qui est la quantité que l’on souhaite connaître mais qui ne peut pas être observée directement dans les données, et \(\hat{\beta}\), qui est une variable aléatoire qui dépend du tirage de multiples observations, et qui correspond à une tentative de reconstruction de \(\beta\) à partir des données observées.
Le fragment de code suivant permet de vérifier sur un cas simple que les coefficients renvoyés par la fonction pré-implémentée de R sont bien estimés par l’estimateur des moindres carrés ordinaires tel qu’il est défini plus haut.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On estime la régression du salaire horaire sur l'éducation et l'âge
reg_wage_educ_age<-lm(wage~education + age,
data=CPS)
reg_wage_educ_age##
## Call:
## lm(formula = wage ~ education + age, data = CPS)
##
## Coefficients:
## (Intercept) education age
## -5.5342 0.8211 0.1050#On construit la matrice X
matrice_covariables<-as.matrix(cbind(rep(1,
nrow(CPS)),
CPS[,
c("education",
"age")]))
#On peut vérifier que X ressemble bien à la matrice que l'on pense
head(matrice_covariables)## V1 education age
## [1,] 1 8 35
## [2,] 1 9 57
## [3,] 1 12 19
## [4,] 1 12 22
## [5,] 1 12 35
## [6,] 1 13 28#On calcule X'X : c'est bien une matrice 3*3
XprimeX<-t(matrice_covariables)%*%matrice_covariables
XprimeX## V1 education age
## V1 534 6952 19669
## education 6952 94152 253613
## age 19669 253613 797769#On calcule X'Y : c'est bien un vecteur de dimension 3 (ou une matrice de taille
# 3*1)
XprimeY<-t(matrice_covariables)%*%as.matrix(CPS$wage)
XprimeY## [,1]
## V1 4818.85
## education 65471.33
## age 183178.61#On multiple à gauche X'Y par l'inverse de X'X
estimateurMCO<-solve(XprimeX)%*%XprimeY
#On vérifie que l'on retombe bien sur les coefficients estimés par lm
all.equal(as.numeric(estimateurMCO),
as.numeric(reg_wage_educ_age$coefficients))## [1] TRUE2.9.3 Précision de l’estimateur des moindres carrés ordinaires
Les paragraphes précédents montrent que dans la limite d’un nombre infini d’observations, la variable aléatoire \(\hat{\beta}:=(\mathbf{X}'\mathbf{X})^{-1}\mathbf{X}'\mathbf{Y}\) s’identifie au vecteur \(\beta\) de \(\mathbb{R}^d\). La question suivante est de quantifier les fluctuations de cette variable aléatoire autour de cette valeur afin de pouvoir examiner la précision, c’est-à-dire en somme la qualité des inférences que l’on peut faire sur \(\beta\) à partir de \(\hat{\beta}\).
À retenir
Lorsque le nombre d’observations tend vers l’infini, la loi de l’estimateur des moindres carrés ordinaires s’identifie à une loi normale multidimensionnelle centrée (c’est-à-dire d’espérance nulle) et de matrice de variance-covariance (i) proportionnelle à l’inverse du nombre d’observations et (ii) à un terme qui ne dépend que de la distribution jointe des variables dépendantes et indépendantes.
Ce résultat est particulièrement utile lorsqu’il s’agit de mettre en place des tests de nullité ou d’égalité de certains coefficients, et plus généralement lorsque l’on veut connaître la précision de l’estimation fondée sur cet estimateur. Une démonstration de ce résultat est proposée en Annexe A.11, qui fait également figurer l’expression exacte de la matrice de variance-covariance.
Remarque
Le fait que lorsque le nombre d’observations tend vers l’infini, la matrice de variance-covariance de \(\hat{\beta}\) soit proportionnelle à l’inverse du nombre d’observations signifie que lorsque l’on se place dans le cas d’un grand nombre d’observations, doubler la taille d’échantillon permet de diviser par deux la variance, et donc de réduire d’environ 30% l’ampleur des intervalles de confiance.
2.9.4 Homoscédasticité et hétéroscédasticité
Le résultat précédent est toujours vrai pourvu que la condition de rang soit respectée. En particulier, il ne fait pas d’hypothèse sur la distribution du résidu en dehors de la nullité de l’espérance, ni sur sa distribution jointe avec les variables indépendantes, en dehors de l’hypothèse d’absence de corrélation.
La difficulté dans l’usage du résultat précédent est que la matrice de variance-covariance en question n’est pas observée directement dans les données. D’abord, son expression fait intervenir des espérances et non des moyennes empiriques. Ensuite, elle fait intervenir le résidu \(\epsilon\) qui n’est jamais observé dans les données au contraire de \(X\) et \(Y\).
Si la variable aléatoire \(\epsilon\) n’est jamais observée dans les données, on dispose en revanche de variables aléatoires \(\hat{\epsilon_i}:=Y_i-X_i'\hat{\beta}\) qui peuvent elles être calculées pour chaque observation. Tout le principe de l’estimation de la variance asymptotique de l’estimateur des moindres carrés ordinaires est de simplement remplacer \(\epsilon_i\) par \(\hat{\epsilon_i}\), et les espérances par des moyennes empiriques. L’argument en faveur de cette approche est tout simplement qu’à mesure que le nombre d’observations s’approche de l’infini, \(\hat{\beta}\) s’identifie à \(\beta\), et donc \(\hat{\epsilon_i}=Y_i-X_i'\hat{\beta}\) s’identifie à \(\epsilon_i=Y_i-X_i'\beta\).
Deux approches peuvent être distinguées à partir de là. La première, qui est celle qui est suivie par défaut pour la grande majorité des logiciels de calcul statistique, consiste à faire l’hypothèse d’homoscédasticité, c’est-à-dire à supposer non seulement comme auparavant que la corrélation du terme \(\epsilon\) avec les variables indépendantes \(X\) est nulle comme auparavant, mais encore que \(\epsilon\) et \(X\) sont indépendantes12. Dans ce cas, le terme \(\mathbb{E}[\epsilon^2 \mid X]\) est constant, égal à un réel positif \(\sigma^2\).
La seconde approche consiste à relâcher cette hypothèse, et donc à supposer que l’on est devant un cas d’hétéroscédasticité. L’estimateur de la variance le plus souvent utilisé dans ce cas est parfois appelé d’estimateur sandwich, et les écarts-types obtenus à partir de cette estimation sont souvent appelés les écarts-types robustes à l’hétéroscédasticité.
L’Annexe B.3 détaille la construction de ces estimateurs de la matrice de variance-covariance de l’estimateur des moindres carrés ordinaires.
Avertissement
Utiliser les écarts-types fondés sur l’hypothèse d’homoscédasticité revient à faire une hypothèse très forte sur le problème étudié.
Pour le voir, on peut considérer le cas simple où \(Y\) est une variable dichotomique, par exemple une variable qui vaut 1 si un individu est observé en emploi et 0 sinon, que l’on régresse sur une autre variable dichotomique qui indique le sexe à l’état-civil et une constante : \(Y=\alpha + \beta X_f + \epsilon\). On a vu que dans ce cas le terme \(\alpha + \beta X_f\) coïncide avec l’espérance conditionnelle, c’est-à-dire avec le taux d’emploi pour chaque sexe. Dés lors, \(\epsilon = 1 - \mathbb{E}[Y \mid X_f]\) pour les individus en emploi, et \(\epsilon = - \mathbb{E}[Y \mid X_f]\) sinon, d’où l’on déduit \(\mathbb{E}[\epsilon^2 \mid X_f]=\mathbb{E}[Y \mid X_f]\{1-\mathbb{E}[Y \mid X_f]\}\). En d’autres termes, dans ce cas, faire l’hypothèse d’homoscédasticité revient à supposer que le taux d’emploi des femmes est égal au taux d’emploi des hommes, ou à 1 moins le taux d’emploi des hommes. Cette hypothèse est au total assez peu vraisemblable.
Plus largement, on peut montrer que : \[\mathbb{E}[\epsilon^2 \mid X] = \mathcal{V}(Y \mid X) + \left\{\mathbb{E}[Y \mid X] - X'\beta\right\}^2\] Ainsi, en excluant les cas pathologiques, faire l’hypothèse d’homoscédasticité revient à supposer non seulement que la dispersion de la variable dépendante \(Y\) ne dépend pas de la valeur des variables indépendantes, mais encore que (ii) la valeur prédite \(X'\beta\) s’identifie à l’espérance conditionnelle \(\mathbb{E}[Y \mid X]\). De la sorte, cette hypothèse est logiquement incohérente avec l’usage qui consiste à utiliser la régression linéaire pour agréger des contrastes ou des coefficients hétérogènes entre plusieurs groupes qui est discuté en 2.6.3 et 2.7. Cette hypothèse impose de supposer que l’espérance conditionnelle \(\mathbb{E}[Y \mid X]\) est linéaire en \(X\), ce qui n’est pas évident en dehors du cas de la régression saturée.
Remarque
Dans l’ensemble, on privilégiera donc dans les applications empiriques les écarts-types robustes à l’hétéroscédasticité, qui ont l’avantage de ne pas faire d’hypothèse forte sur la distribution de la variable dépendante. Le calcul en est un peu plus coûteux que pour les écarts-types fondés sur l’hypothèse d’homoscédasticité, mais il reste très accessible avec les moyens informatiques disponibles aujourd’hui.
Le fragment de code suivant illustre la discussion précédente dans le cas de la régression du salaire sur le niveau d’éducation mesurée en années passées dans le système scolaire, à partir des données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On estime la régression du salaire horaire sur l'éducation
reg_wage_educ<-lm(wage~education,
data=CPS)
#L'hypothèse d'homoscédasticité suppose que la dispersion des salaires est la
# même quel que soit le niveau d'éducation
#Cette hypothèse semble peu plausible quand on observe la forme du nuage de
# points : les salaires sont bien plus dispersés pour les individus les plus
# éduqués
#On rajoute juste un peu de bruit à la variable d'éducation pour faciliter la
# visualisation quand il y a plusieurs salariés avec le même niveau
# d'éducation
CPS$jitter_education<-
CPS$education+
(table(CPS$education)[as.character(CPS$education)]>1)*
rnorm(nrow(CPS),sd=0.3)
ggplot(data=CPS,
aes(x=education,
y=wage))+
geom_point(color="black",
size=5,
alpha=0.2,
aes(x=jitter_education))+#nuage de points
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(ylim=c(-5,30))+#choix d'échelle des axes
ylab("Salaire horaire ($ par heure)")+#titre des axes
xlab("Années d'éducation")+
theme(text=element_text(size=32),#taille du texte
strip.text.x = element_text(size=32),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))
#On vérifie cela en estimant l'écart-type du salaire pour chaque niveau
# d'éducation
var_wage_educ<-CPS[,
list(std_wage=sqrt(var(wage))),
by="education"]
ggplot(data=var_wage_educ,
aes(x=education,
y=std_wage))+
geom_point(color="black",
size=5,
alpha=0.2)+#points
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(ylim=c(0,10))+#choix d'échelle des axes
ylab("Écart-type du salaire horaire ($ par heure)")+#titre des axes
xlab("Années d'éducation")+
theme(text=element_text(size=32),#taille du texte
strip.text.x = element_text(size=32),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))## Warning: Removed 4 rows containing missing values (`geom_point()`).#On peut à présent comparer les écarts-types et les intervalles de confiance
# sous l'hypothèse d'homoscédasticité
coeftest(reg_wage_educ)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.745980 1.045454 -0.7135 0.4758
## education 0.750461 0.078734 9.5316 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#Avec ceux que l'on a quand on corrige la matrice de variance-covariance
coeftest(reg_wage_educ,
vcov=vcovHC(reg_wage_educ))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.745980 1.048221 -0.7117 0.477
## education 0.750461 0.084905 8.8389 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#L'hypothèse d'homoscédasticité conduit à sous-estimer l'écart-type du
# coefficient de la variable d'éducation de 7%
1-
sqrt(vcov(reg_wage_educ)["education",
"education"])/
sqrt(vcovHC(reg_wage_educ)["education",
"education"])## [1] 0.072682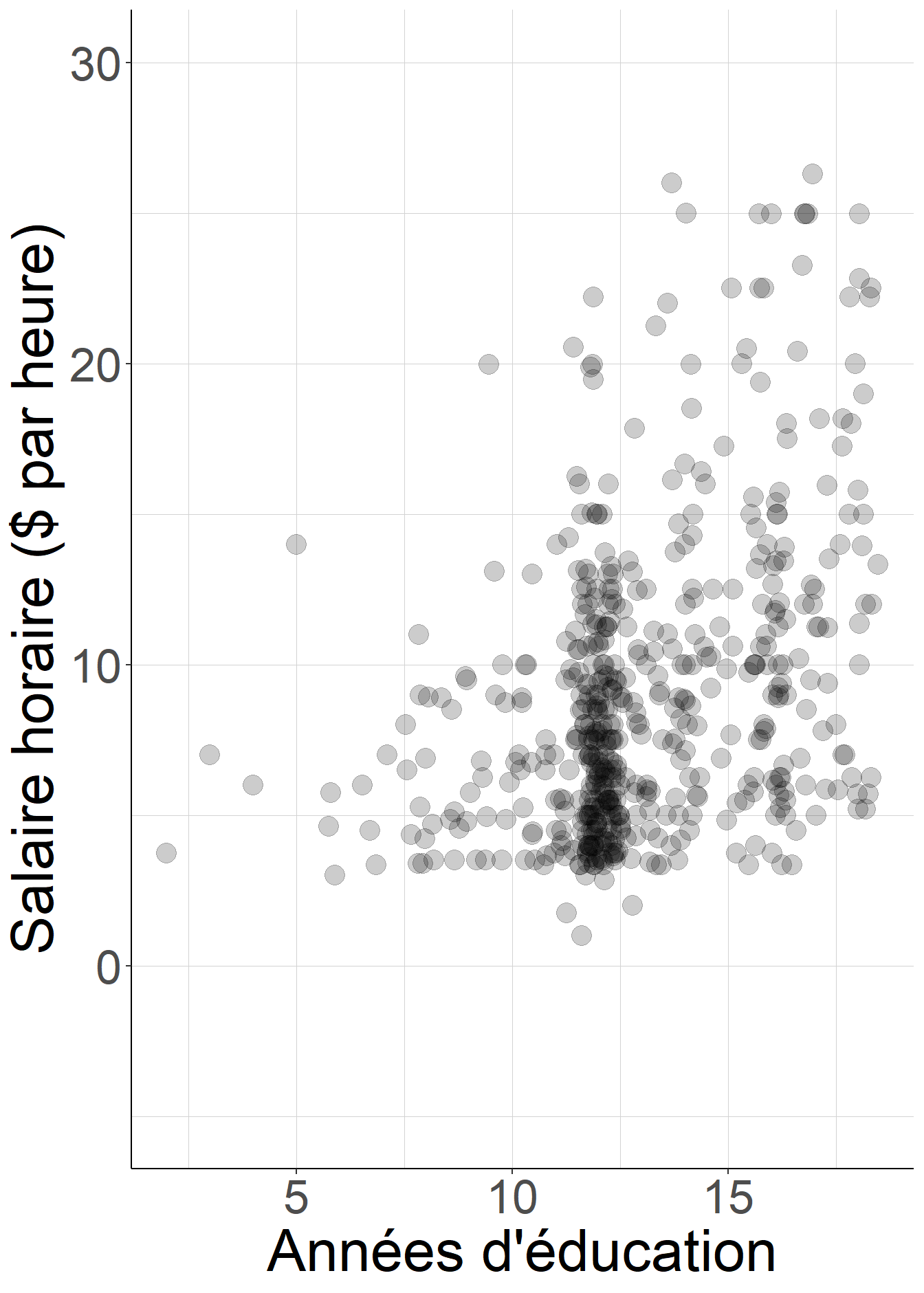
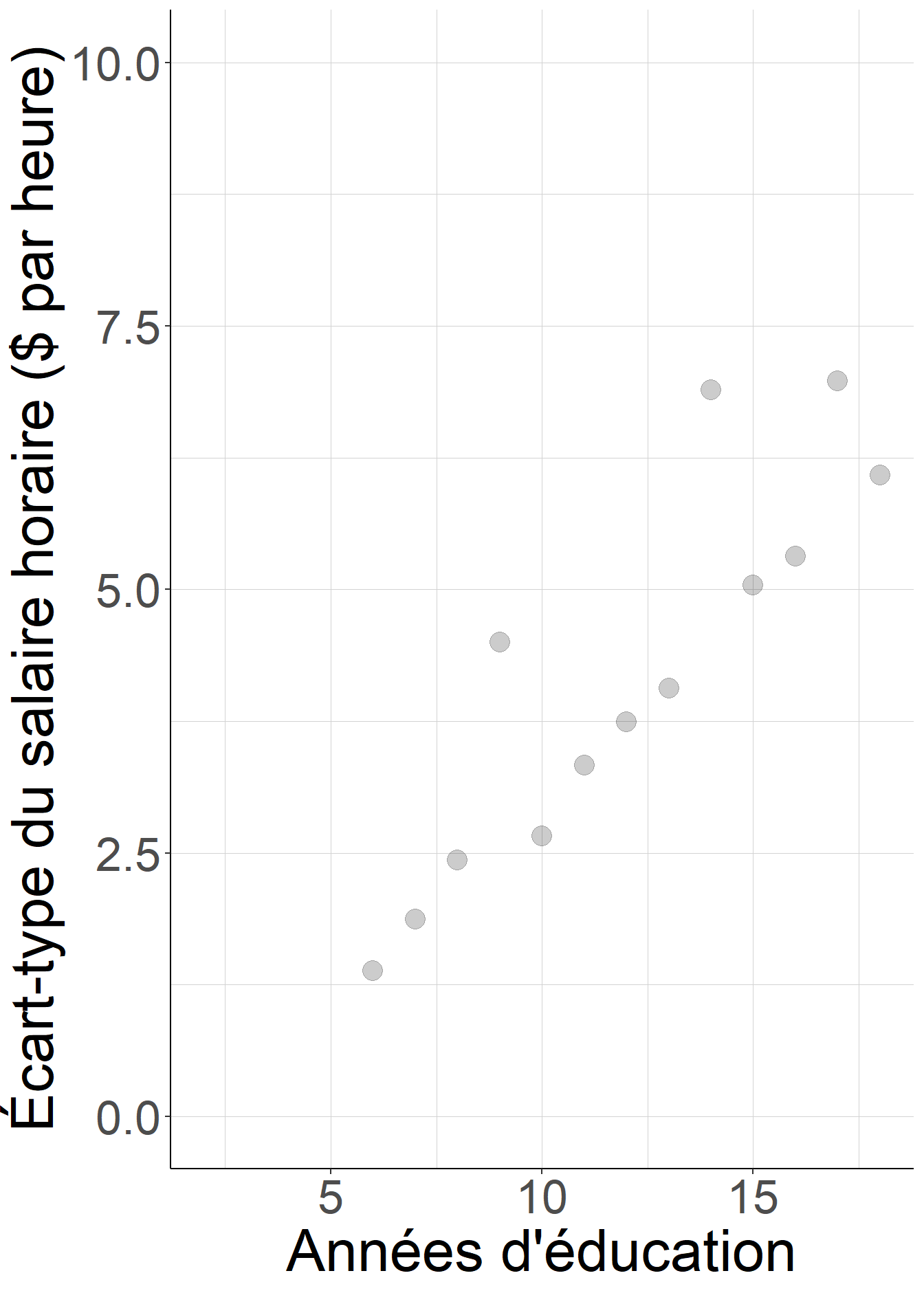
Figure 2.10: L’hypothèse d’homoscédasticité n’est pas plausible : la dispersion des salaires horaires n’est pas la même pour les individus ayant passé le plus de temps dans le système scolaire et pour ceux qui ont passé le moins de temps.
Le fragment de code suivant examine les conséquences du choix de méthode de calcul des écarts-types à partir de données simulées pour lesquelles (i) la dispersion de la variable dépendante est la même pour tous les niveaux de variable indépendante, mais (ii) l’espérance conditionnelle et la droite de régression ne s’identifient parce que l’espérance conditionnelle présente une nette non-linéarité.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
set.seed(20220921)
#On simule 10000 observations de la variable indépendantes à partir d'une loi
# normale centrée réduite, et on fait de même pour créer une autre variable
# qui va jouer le rôle de résidu
simuldat<-data.table(c(rnorm(10000)),
c(rnorm(10000)))
colnames(simuldat)<-c("x",
"epsilon")
#On crée à partir de ces deux variables une variable dépendante y. Cette
# variable s'écrit comme la somme d'une fonction quadratique de x et d'un résidu
# indépendant de x.
#Ainsi, la variance conditionnelle de la variable indépendante V(epsilon | x)
# ne dépend pas de x, mais l'espérance conditionnelle E[y2 | x] est une fonction
# quadratique et n'appartient pas à l'ensemble des fonctions affines de x.
simuldat[,
y:=5+2*x-1.5*x^2+epsilon]
#On régresse la variable dépendante y sur la variable indépendante x
reg<-lm(y~x,
data=simuldat)
#On peut à présent comparer les écarts-types et les intervalles de confiance
# sous l'hypothèse d'homoscédasticité
coeftest(reg)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.510262 0.023797 147.508 < 2.2e-16 ***
## x 1.971879 0.023793 82.877 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#Avec ceux que l'on a quand on corrige la matrice de variance-covariance
coeftest(reg,
vcov=vcovHC(reg))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.510262 0.023823 147.347 < 2.2e-16 ***
## x 1.971879 0.048984 40.256 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#L'hypothèse d'homoscédasticité conduit à sous-estimer l'écart-type du
# coefficient de la variable indépendante de plus de moitié
1-
sqrt(vcov(reg)["x",
"x"])/
sqrt(vcovHC(reg)["x",
"x"])## [1] 0.514273#On visualise les nuages de points, ainsi que les droites de régression et
# l'espérance conditionnelle pour les deux cas considérés.
nuage<-ggplot(data=simuldat,
aes(x=x))+
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(xlim=c(-2.5,2.5),
ylim=c(-7.5,12.5))+#choix d'échelle des axes
ylab("Variable dépendante")+#titre des axes
xlab("Variable indépendante")+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))
nuage+
geom_point(aes(y=y),
alpha=0.2,
size=5)+#le nuage de points
geom_line(color="red",
linewidth=3,
aes(y=reg$coefficients["(Intercept)"]+
reg$coefficients["x"]*x))+#la droite de régression
geom_line(aes(y=5+2*x-1.5*x^2),
color="red",
linetype="dashed",
linewidth=3)+#l'espérance conditionnelle
annotate("text",
x=-2,
y=10,
hjust=0,
label=paste0(paste0("Ecart-type par défaut : ",
round(sqrt(vcov(reg)["x",
"x"]),
digits=2),
"\n"),
paste0("Ecart-type robuste : ",
round(sqrt(vcovHC(reg)["x",
"x"]),
digits=2))),
size=4)#afficher les écarts-types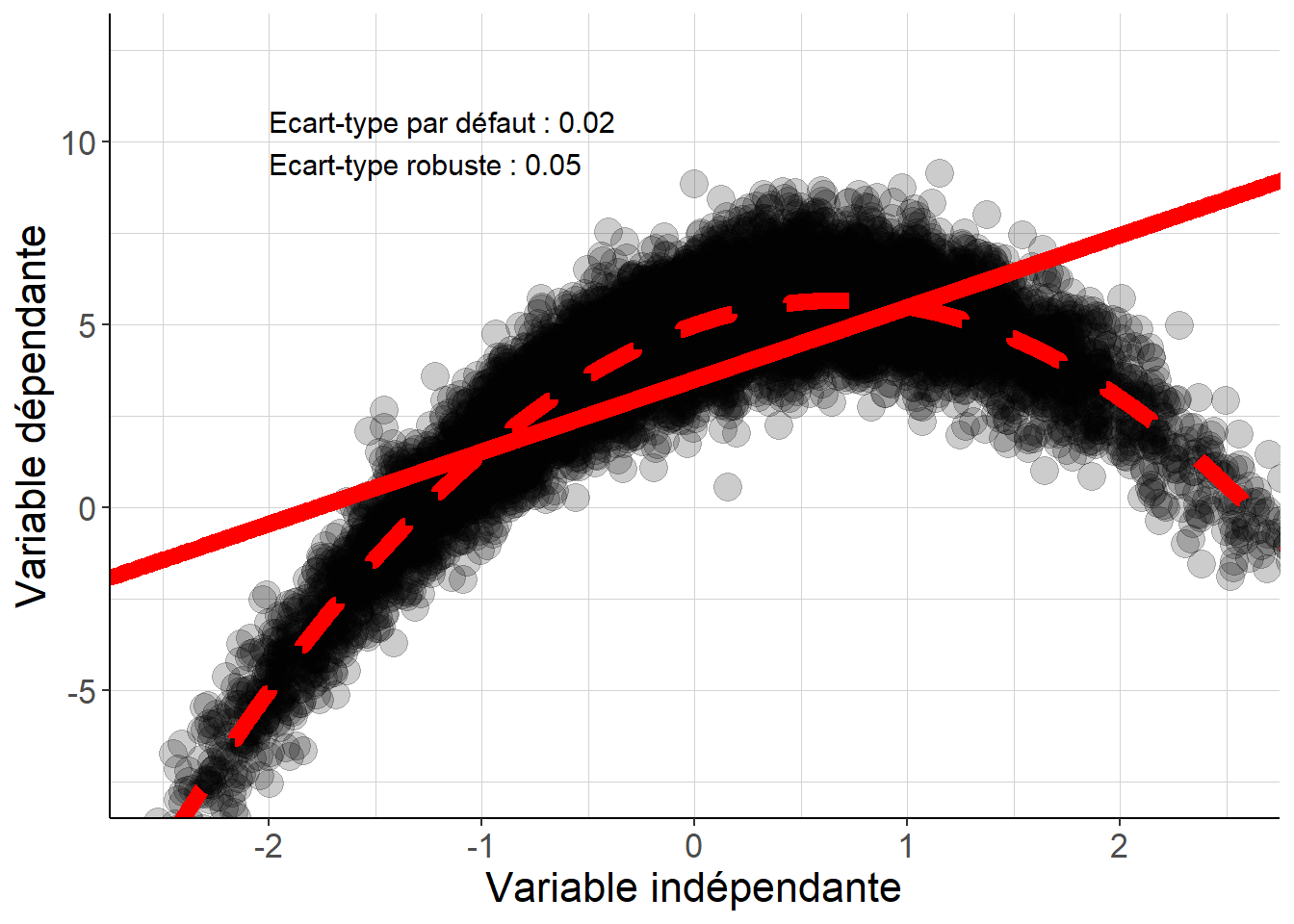
Figure 2.11: Même lorsque la dispersion de la variable dépendante est la même pour tous les niveaux de la variable indépendante, si l’espérance conditionnelle présente des non-linéarités, faire l’hypothèse d’homoscédasticité conduit à nettement sous-estimer l’incertitude qui porte sur les coefficients de la régression linéaire.
2.9.5 Données en clusters
Tout ce qui précède repose sur l’hypothèse que dans le tirage que l’on effectue en vue d’estimer le vecteur \(\beta\), les observations sont indépendantes entre elles. Cette hypothèse peut être mise à mal dans plusieurs cas que l’on rencontre fréquemment dans la pratique. On peut considérer par exemple le travail de Hamermesh et Parker (2005), qui considèrent la régression du score attribué aux enseignants par leurs étudiants de l’Université du Texas à Austin lors de l’évaluation de leur enseignement, sur un score composite de beauté attribué indépendamment par six étudiants, ainsi que quelques autres variables destinées à décrire ces enseignants.
La variable indépendante qui concentre l’attention dans ce travail, à savoir le score de beauté, est calculé au niveau de chaque enseignant. En revanche, les données employées sont agrégées au niveau de chaque cours donné par chaque enseignant. Ainsi, comme chaque enseignant est susceptible de donner plusieurs cours et donc d’être évalué plusieurs fois, la structure des données fait apparaître une corrélation entre les valeurs des variables indépendantes sur des observations différentes. Par exemple, si ce score de beauté était mesuré avec erreur, par exemple parce qu’il y a des erreurs de saisie, alors cette erreur doit être la même pour toutes les lignes concernant le même enseignant.
Le fragment de code suivant permet de visualiser cette structure de cluster dans les données utilisées pour cet article.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
library(viridis,
quietly=TRUE)
#On charge dans un premier temps les données nécessaires
data("TeachingRatings")
TeachingRatings<-data.table(TeachingRatings)
#Pour visualiser un peu le problème
#Réordonner les enseignants selon leur beauté estimée
TeachingRatings$prof<-factor(TeachingRatings$prof,
levels=
setorder(unique(TeachingRatings[,
c("prof",
"beauty")]),
beauty)$prof)
ggplot(data=TeachingRatings,
aes(x=beauty,
y=eval,
color=prof,
group=prof))+
theme_classic()+#supprime l'arrière-plan gris par défaut
coord_cartesian(xlim=c(-1.5,2),
ylim=c(2,5))+#choix d'échelle des axes
xlab("Score de beauté de l'enseignant")+#titre des axes
ylab("Evaluation par les étudiants \nayant suivi le cours")+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))+
geom_point()+
geom_line()+
scale_color_viridis(discrete=TRUE,
option="magma",
end=0.9)+
theme(legend.position = "none")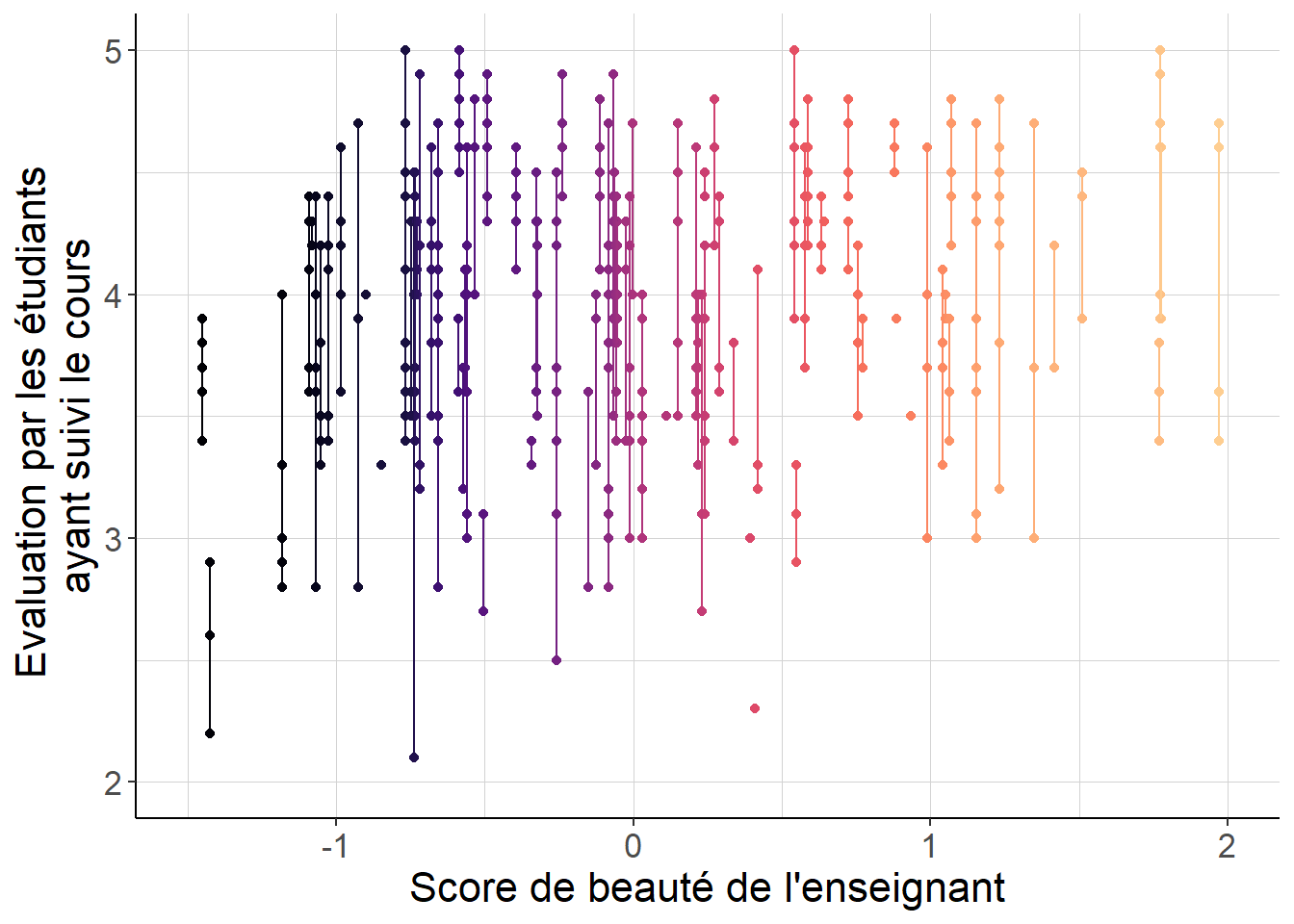
Figure 2.12: Le score composite de beauté est le même pour toutes les observations associées à l’évaluation d’un enseignant par les étudiants ayant suivi un de ses cours. De ce fait, si ce score est par exemple reporté avec erreur, cette erreur est la même pour toutes les observations associées à chacun des cours donnés par le même enseignant, qui ne peuvent plus être supposées indépendantes. Les écarts-types usuels ne peuvent plus être utilisés dans cette situation.
Ce problème se rencontre fréquemment dans la pratique, essentiellement pour deux raisons différentes.
La première est celle que l’on rencontre dans l’exemple présenté ci-dessus : on peut être intéressé par le coefficient qui porte sur une variable qui n’est pas assignée au niveau de chaque observation individuelle, mais à un niveau plus agrégé. Par exemple, on pourrait imaginer régresser le salaire de chaque salarié sur un ensemble de variables dichotomiques indiquant la couverture de l’entreprise par une convention collective. Dans ce cas, si cette couverture par une convention collective est mesurée avec erreur, cette erreur sera la même pour tous les salariés de la même entreprise, et l’on ne peut donc plus supposer que l’hypothèse d’indépendance est respectée.
Un autre cas dans lequel on souhaite pouvoir relâcher l’hypothèse d’indépendance est celle des sondages à plusieurs degrés. Supposons par exemple que l’on étudie une enquête sur les élèves dont le protocole consiste à tirer dans un premier temps des établissements scolaires, puis à tirer ensuite à l’intérieur de chaque établissement sélectionné plusieurs élèves. Dans ce cas, l’hypothèse d’indépendance qui conduit à considérer que l’on a autant d’observations que d’élèves reflète mal l’incertitude qui émerge de la structure du sondage. On a bien l’intuition que pour extraire une information portant sur toute la population des élèves au niveau national, il ne revient pas du tout au même de tirer 2 fois 500 élèves dans 2 établissements différents, ou 500 fois 2 élèves dans 500 établissements différents. L’hypothèse d’indépendance conduit pourtant à regarder les deux protocoles de la même façon puisque dans ce cas la variance asymptotique de \(\hat{\beta}\) fait toujours figurer le terme \(\frac{1}{n}\).
La solution à ce problème consiste à supposer que l’on peut maîtriser sa gravité en découpant la population d’intérêt en plusieurs groupes ou clusters, tels que l’on puisse supposer que les observations de deux observations appartenant à deux groupes différents sont bien indépendantes, mais que cela n’est pas le cas si elles appartiennent à deux groupes identiques. En d’autres termes, cette solution ne vise pas à régler des problèmes très généraux de dépendance mutuelle qui aboutiraient à conclure que le concept d’indépendance probabiliste n’a de toute façon aucun rôle à jouer en sciences sociales. Elle vise plutôt à quantifier la gravité du problème en supposant que celui-ci est plus marqué dans certaines situations que dans d’autres. Ainsi, dans l’exemple du premier paragraphe, on fera l’hypothèse que les observations relatives à deux salariés sont indépendantes s’ils appartiennent à deux entreprises différentes, mais qu’elles ne sont pas indépendantes s’ils appartiennent à la même entreprise.
Sous ces hypothèses, lorsque l’on se place dans un cas où le nombre de clusters est suffisamment grand, on dispose de nouveau de résultats asymptotiques portant sur la précision de l’estimateur des moindres carrés ordinaires
À retenir
Lorsque le nombre de clusters tend vers l’infini, la loi de l’estimateur des moindres carrés ordinaires s’identifie à une loi normale multidimensionnelle centrée (c’est-à-dire d’espérance nulle) et de matrice de variance-covariance (i) proportionnelle à l’inverse du nombre de clusters et (ii) à un terme qui ne dépend que de la distribution jointe des variables dépendantes et indépendantes et de la corrélation des ces variables entre observations appartenant au même cluster.
Une démonstration de ce résultat est proposée en Annexe A.12. L’Annexe B.3.3 examine avec encore davantage de détail l’estimation de la matrice de variance-covariance de l’estimateur de moindres carrés ordinaires sous ces nouvelles hypothèses.
Le fragment de code suivant reprend l’exemple de Hamermesh et Parker (2005) en comparant les écarts-types obtenus sous l’hypothèse habituelle d’indépendance d’une part, et en relâchant cette hypothèse d’autre part. Cette comparaison permet de montrer que faire appel à l’hypothèse d’indépendance conduirait dans ce cas à des écarts-types trop faibles, et donc à une sous-estimation de l’incertitude qui pèse sur les résultats.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
#On charge dans un premier temps les données nécessaires
data("TeachingRatings")
TeachingRatings<-data.table(TeachingRatings)
#On réplique Hamermesh and Parker, 2005, Table 3
reg_eval<-lm(eval ~ beauty +
gender +
minority +
native +
tenure +
division +
credits,
weights = students,
data = TeachingRatings)
#On considère d'abord l'inférence robuste à l'hétéroscédasticité
coeftest(reg_eval,
vcov=vcovHC(reg_eval))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.223142 0.066182 63.8106 < 2.2e-16 ***
## beauty 0.274805 0.036160 7.5997 1.708e-13 ***
## genderfemale -0.238993 0.058767 -4.0668 5.617e-05 ***
## minorityyes -0.248937 0.094617 -2.6310 0.008802 **
## nativeno -0.252713 0.103409 -2.4438 0.014911 *
## tenureyes -0.135923 0.062073 -2.1897 0.029051 *
## divisionlower -0.045895 0.062249 -0.7373 0.461335
## creditssingle 0.686507 0.120289 5.7071 2.074e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#On peut vérifier que le score de beauté est bien le même pour plusieurs cours
# du même enseignant
#Exemple d'un enseignant qui donne 5 cours différents
all.equal(TeachingRatings[prof==56][1]$beauty,
TeachingRatings[prof==56][5]$beauty)## [1] TRUE#On considère l'inférence une fois prise en compte cette structure de dépendance
# dans les données
coeftest(reg_eval,
vcov = vcovCL,
cluster = TeachingRatings$prof)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.223142 0.097456 43.3339 < 2.2e-16 ***
## beauty 0.274805 0.058726 4.6794 3.800e-06 ***
## genderfemale -0.238993 0.085124 -2.8076 0.005206 **
## minorityyes -0.248937 0.111681 -2.2290 0.026301 *
## nativeno -0.252713 0.133994 -1.8860 0.059930 .
## tenureyes -0.135923 0.094226 -1.4425 0.149845
## divisionlower -0.045895 0.100740 -0.4556 0.648912
## creditssingle 0.686507 0.165541 4.1471 4.019e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#Ne pas prendre en compte cette structure de dépendance conduit à sous-estimer
# l'écart-type du coefficient sur le score de beauté de plus de 38%
1-
sqrt(vcovHC(reg_eval)["beauty",
"beauty"])/
sqrt(vcovCL(reg_eval,
cluster=TeachingRatings$prof)["beauty",
"beauty"])## [1] 0.384267Remarque
La motivation pour le choix d’un niveau ou d’un autre de clustering n’est pas toujours évidente. En règle générale, pour les données d’enquête par sondage, il est possible de connaître le plan de sondage et donc de savoir s’il faut prendre en compte des degrés supplémentaires de sondage dans l’inférence. Lorsque la motivation est liée à la structure de dépendance dans les données indépendamment de ces considérations sur les plans de sondage, la motivation n’est pas toujours aussi claire. La littérature récente suggère que le choix doit en fait dépendre de la question à laquelle on cherche à répondre à l’aide de la régression. Lorsqu’il s’agit d’une question causale, Abadie et al. (2022) conseillent de considérer que le niveau auquel le traitement est assigné doit être considéré comme le bon niveau de clustering. C’est bien ce qui est fait dans le cas de l’exemple empirique considéré : si on interprète la beauté de l’enseignant comme un traitement, alors celle-ci est assignée à niveau de l’enseignant et pas au niveau du cours, et c’est donc bien au niveau de l’enseignant qu’il faut se mettre dans le clustering.
Remarque
Il peut arriver qu’il y ait plusieurs niveaux non-imbriqués les uns dans les autres pour lesquels il serait pertinent de considérer des clusters. Cela pourrait être le cas par exemple lorsque l’on considère des salariés qui peuvent travailler pour plusieurs entreprises, qui elles-mêmes emploient plusieurs salariés, et que l’on s’intéresse à des données de salaire au niveau de couples salariés-employeurs. Dans ce cas, certains logiciels de calcul statistique proposent de faire le calcul d’une matrice de variance-covariance qui prend en compte ces multiples niveaux de dépendance. Cela étant, ce calcul est parfois problématique, et Davezies, D’Haultfœuille et Guyonvarch (2021) montrent que la solution théoriquement la plus pertinente est (i) d’estimer la matrice de variance-covariance séparément pour chaque niveau de clustering et (ii) de sommer ces matrices de variance-covariance pour obtenir la matrice de variance-covariance correcte.