5.6 Utilisation du score de propension : en pratique

Il s’agit à présent, une fois le score de propension estimé, de l’utiliser en s’appuyant sur une des trois techniques proposées : stratification, appariement ou repondération. Lorsque l’on passe de l’application un peu mécanique justifiée par la théorie à l’application pratique à des données empiriques, chacune de ces techniques exige de se poser des questions différentes sur ce que l’on fait.

Un des enjeux importants dans l’utilisation de ces techniques est que, maintenant que l’on a accepté une première forme d’extrapolation dans l’estimation du score de propension, il faut accepter une deuxième forme d’extrapolation dans son utilisation. Il n’est plus question ici en fait d’utiliser les valeurs exactes du score de propension pour définir les strates ou les individus à apparier. L’idée est plutôt d’utiliser les valeurs du score de propension comme une mesure de proximité entre individus : deux individus sont d’autant plus susceptibles de pouvoir former une comparaison intéressant que les valeurs du score de propension qui leur sont associées sont plus proches. On va ainsi constituer des strates et des couples d’individus dont les valeurs estimées du score de propension sont proches, et non plus rigoureusement égales.

On va tenter d’appliquer ces trois techniques au même exemple, celui de Gerber et Green (2000) et Imai (2005), en s’approchant autant que possible du travail effectivement réalisé par Imai (2005). Dans les trois cas, tout commence encore une fois par l’estimation du score de propension. Cette fois on ne se limite plus à l’hypothèse très simplificatrice selon laquelle le seul défaut de l’expérience aléatoire contrôlée initiale tient à ce que la probabilité de recevoir un appel téléphonique différe d’un quartier à l’autre. Comme Imai (2005), on va considérer tout un ensemble d’autres variables observables : comportement électoral passé, type de ménage, âge etc.

Avant de passer à l’utilisation des différentes techniques, le fragment de code suivant propose simple de faire l’estimation du score de propension, puis de représenter l’histogramme du score de propension pour chaque groupe défini par l’intervention pour s’assurer de la validité de l’hypothèse de support commun.

library(data.table)
library(ggplot2)
library(Matching)

#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)

#On estime le score de propension avec un modèle logit
pscore_estimates<-glm(PHN.C1 ~ PERSONS + 
                        WARD +
                        AGE +
                        MAJORPTY +
                        VOTE96.0 +
                        VOTE96.1 +
                        NEW + 
                        AGE2 +
                        PERSONS*VOTE96.0 + 
                        PERSONS*NEW,
                      data=GerberGreenImai,
                      family=binomial(link=logit))$fitted.values

#On remet ce score de propension estimé dans la table initiale
GerberGreenImai<-cbind(GerberGreenImai,
                       pscore_estimates)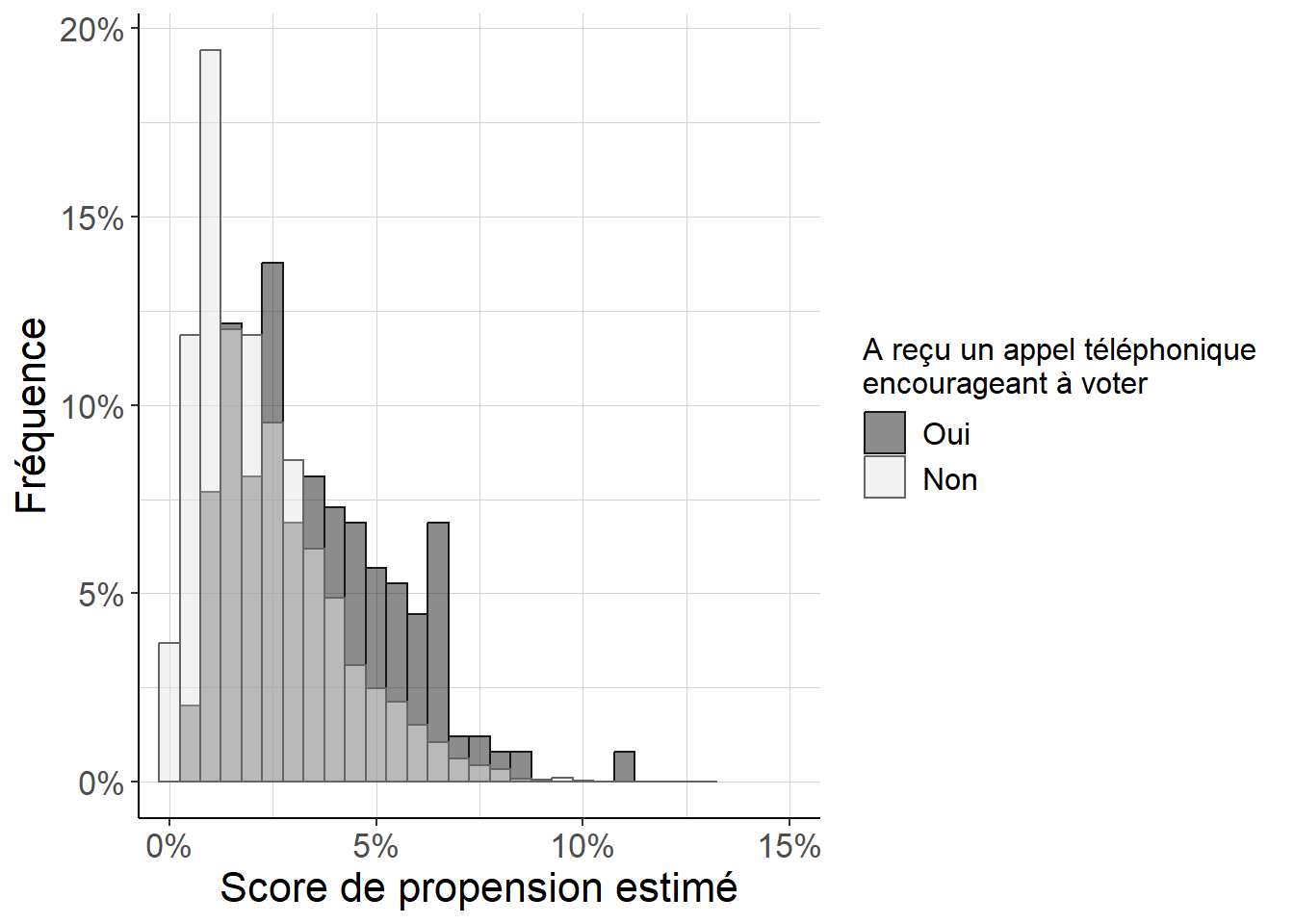

Figure 5.10: Histogramme répliquant Imai (2005) (figure 8). Parce que l’on est, en dépit de ses défauts, dans un cas proche d’une expérience aléatoire contrôlée avec une faible probabilité de recevoir un appel téléphonique appelant à voter, on peut voir que (i) les scores de propension sont faibles pour tous les individus, et (ii) les différences entre individus ayant reçu ou n’ayant pas reçu d’appel téléphonique restent relativement faibles. Cependant, on voit aussi que le score de propension est également en général plus important pour les individus ayant reçu un appel téléphonique que pour les autres.

5.6.1 Stratification

En pratique, l’utilisation de la stratification pour estimer les effets causaux moyens de l’intervention revient à utiliser les valeurs estiméees du score de propension pour délimiter des strates au sein desquelles on compare simplement les individus selon qu’ils ont fait ou non l’objet de l’intervention. Cette approche est justifiée en théorie par le fait que si l’on utilisait les vraies valeurs du score de propension pour délimiter ces strates de façon exacte (une valeur du score de propension différente pour chaque strate), alors à l’intérieur de ces strates, la situation serait équivalente à celle d’une expérience aléatoire contrôlée, ou d’une expérience naturelle.

On ne va pas ici définir les strates de façon exacte : la raison pour cela est que si l’on utilise par exemple des variables de conditionnement continues, alors en général les valeurs estimées du score de propension seront différentes pour tous les individus, de sorte que les strates exactes ne contiendront qu’un individu et ne permettront pas de faire la comparaison pertinente. Il faut donc définir des strates plus larges, c’est-à-dire des strates qui contiennent plusieurs valeurs estimées possibles du score de propension.

Tout l’intérêt du score de propension est ici de pouvoir être utilisé comme une mesure de proximité entre individus : on va donc définir des strates qui regroupent des individus pour lesquels les valeurs estimées du score de propension sont sinon exactement égales, du moins relativement proches. Pour ce faire, ces strates sont définies comme des intervalles avec des bornes \(\underline{p}\) et \(\overline{p}\), de sorte qu’une strate rassemble tous les individus pour lesquels la valeur estimée du score de propension \(\hat{p}(X_i)\) est comprise entre \(\underline{p}\) et \(\overline{p}\).

L’enjeu est donc de déterminer :

1. le nombre de strates à considérer, et ;
2. les bornes qui séparent chaque strates de ses voisines.

Il est courant de se contenter de 5 strates, et de définir ces bornes à partir des quantiles (et plus précisément des quintiles) de la distribution des valeurs estimées du score de propension. D’autres approches, davantage guidées par les données elles-mêmes peuvent pourtant être proposés (Imbens (2015)).

Le fragment de code suivant met en place cette stratification en 5 strates définies par les valeurs des quintiles sur l’exemple emprunté à Imai (2005), pour lequel on a au préalable estimé le score de propension. On commence par utiliser ces strates pour tester la propriété équilibrante du score de propension, puis on procède à l’estimation des effets causaux moyens du score de propension à proprement parler.

#On définit les strates à partir des quintiles de la distribution du score de
# propension
quintiles<-quantile(GerberGreenImai$pscore_estimates,
                    probs=0.2*c(1:4))
GerberGreenImai[,
                strates_pscore:=findInterval(x=pscore_estimates,
                                             vec=quintiles)]

#Au sein de chacune de ces strates, on va comparer du point de vue de la valeur
# des variables de conditionnement les individus selon qu'ils ont ou qu'ils 
# n'ont pas reçu un appel téléphonique, et on va réagréger ces écarts avec
# des poids proportionnels à la taille de chaque strate dans la population
# (ici comme les strates sont définies par les valeurs des quintiles elles ont
# toutes le même poids).
#On va aussi comparer cet écart estimé via la stratification à l'écart brut
# sans stratification

#Fonction qui renvoie la différence moyenne entre le groupe qui fait
# l'objet de l'intervention et celui qui n'en fait pas l'objet
diff_moy<-function(variable,
                            groupe_intervention,
                            poids=NULL){
  
  if(is.null(poids)){
    
    (sum(groupe_intervention*variable)/
       sum(groupe_intervention)-
       (sum((1-groupe_intervention)*variable))
     /sum(1-groupe_intervention))
    
  }
  
  else{
    
    (sum(poids*groupe_intervention*variable)/
       sum(poids*groupe_intervention)-
       (sum(poids*(1-groupe_intervention)*variable))
     /sum(poids*(1-groupe_intervention)))
    
  }
  
}

#On applique cette fonction aux variables de conditionnement, d'abord sans 
# stratification, ensuite avec la stratification

#On définit les variables de conditionnement sur lesquelles on va tester 
# la propriété équilibrante du score de propension 
variables_conditionnement<-c("PERSONS",
                             "AGE",
                             "MAJORPTY",
                             "VOTE96.0",
                             "VOTE96.1",
                             "NEW")

#Sans stratification : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement
contrastes_bruts<-GerberGreenImai[, 
                                  lapply(X=.SD,
                                         FUN=function(x){
                                           list(
                                             diff_moy(
                                               variable=x,
                                               groupe_intervention=PHN.C1),
                                             sqrt(0.5*var(x)))
                                           }),
                                  .SDcols=variables_conditionnement]
contrastes_bruts[,
                 stat:=c("diff_moy",
                         "spread")]
contrastes_bruts<-melt(contrastes_bruts,
                      variable.name="variable",
                      value.name="valeur",
                      id.vars="stat")

#Avec stratification
#On commence par calculer la différence moyenne dans chaque strate
contrastes_par_strates<-GerberGreenImai[, 
                                  lapply(
                                    X=.SD,
                                    FUN=function(x){
                                      diff_moy(variable=x,
                                               groupe_intervention=
                                                 PHN.C1)
                                      }),
                                  .SDcols=variables_conditionnement, 
                                  by=c("strates_pscore")
                                  ]

#Ensuite on prend la moyenne de ces différences moyennes (comme on a défini
# les strates à partir des quintiles, elles ont toutes le même poids dans la
# population et on n'a pas besoin de spécifier les poids)
contrastes_agreges_stratifies<-
  contrastes_par_strates[,
                         lapply(X=.SD,
                                mean),
                         .SDcols=variables_conditionnement]
contrastes_agreges_stratifies[,
                              stat:="diff_moy"]
contrastes_agreges_stratifies<-
  melt(contrastes_agreges_stratifies,
       id.vars="stat",
       value.name="valeur",
       variable.name="variable")

#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
#On crée une fonction qui fait ça et qui sera utile pour les autres techniques
contrastes_propre<-function(contrastes_bruts_dat,
                            contrastes_pscore_dat){
  
  contrastes_propre_dat<-rbind(contrastes_bruts_dat,
                               contrastes_pscore_dat,
                               idcol="etape")
  
  contrastes_propre_dat<-rbind(contrastes_propre_dat,
                               contrastes_propre_dat[stat=="spread",
                                                     -c("etape")],
                               fill=TRUE)[is.na(etape),
                                          etape:=2]
  
  contrastes_propre_dat<-
    contrastes_propre_dat[,
                          list(diff_std=
                                 sum(as.numeric(stat=="diff_moy")*
                                       as.numeric(valeur))/
                                 sum(as.numeric(stat=="spread")*
                                       as.numeric(valeur))),
                          by=c("variable",
                               "etape")]
  
}

contrastes_stratification<-contrastes_propre(contrastes_bruts,
                                             contrastes_agreges_stratifies)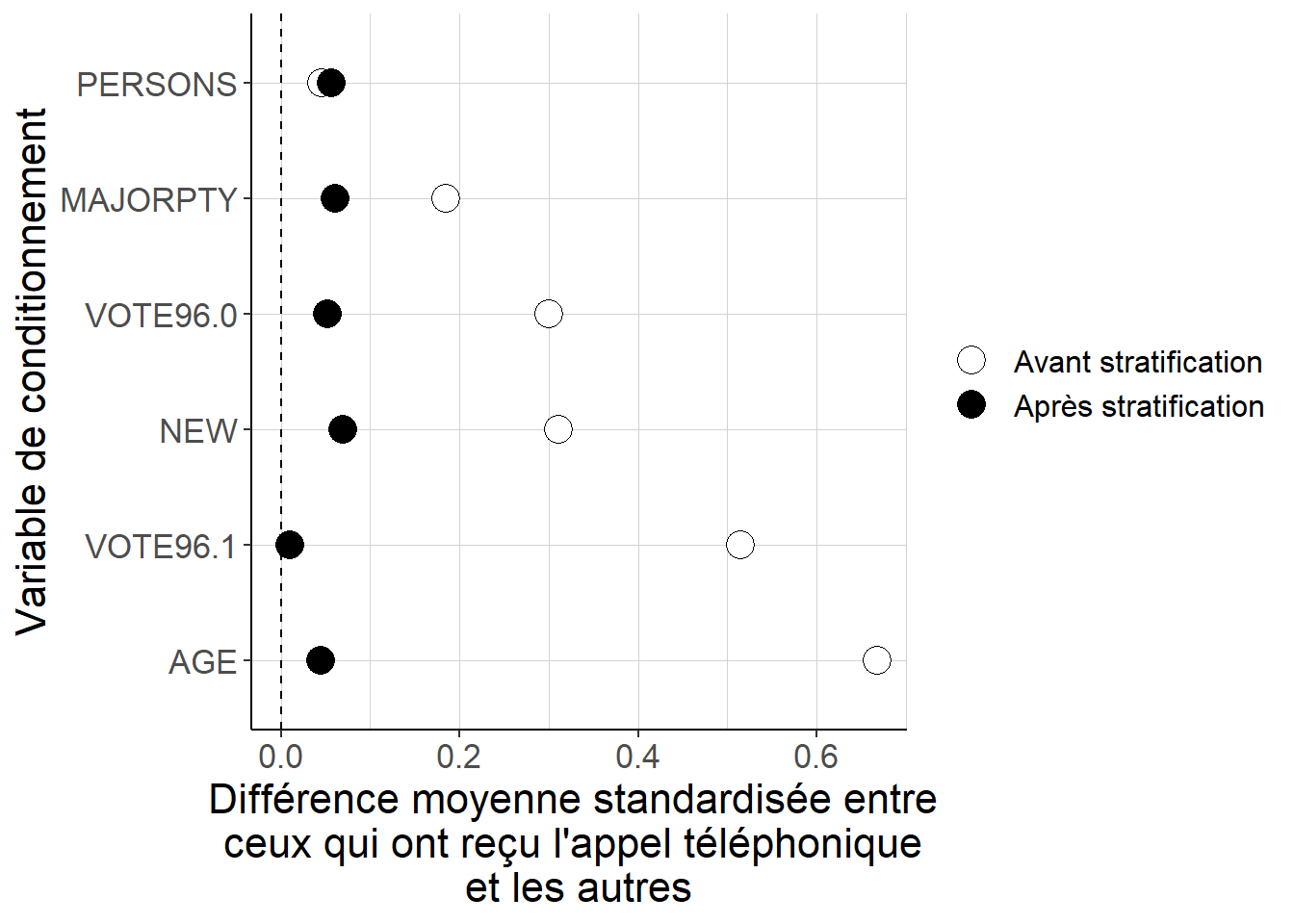

Figure 5.11: Alors que les différences quant aux valeurs des variables de conditionnement entre les individus qui ont reçu l’appel téléphonique et les autres peuvent être importantes lorsque l’on considère les données brutes, constituer 5 strates à partir des quintiles des valeurs estimées du score de propension permet de réduire de façon importante ces écarts. Cela suggère que la stratification permet de mieux équilibrer les deux groupes du point de vue de ces variables de conditionnement.

Mettre à l’épreuve la propriété équilibrante du score de propension en utilisant la technique de stratification permet de vérifier qu’une fois que l’on se place à l’intérieur de strates définies par les quintiles des valeurs estimées du score de propension, les différences observables entre les individus ayant reçu un appel téléphonique et les autres sont beaucoup plus faibles que lorsque l’on considère les écarts bruts entre ces deux groupes. En toute rigueur, ces différences ne sont toutefois pas nulles même après l’étape de stratification.

Après cette étape préalable, on peut passer à l’estimation des effets causaux moyens à proprement parler. Pour ce faire, on peut simplement commencer par calculer l’écart du taux de partcipation entre ceux qui ont reçu l’appel téléphonique incitant à voter et les autres à l’intérieur de chaque strate, puis prendre la moyenne de ces différences (avec des poids proportionnels à la taille de chaque strate dans la population : ici comme les strates sont définies à partir des quintiles des valeurs estimées du score de propension ces poids sont tous égaux).

#On commence par estimer la différence de taux de participation électorale
# à l'intérieur de chaque strate
effet_par_strate<-GerberGreenImai[,
                                  lapply(X=.SD,
                                         FUN=function(x){
                                           diff_moy(
                                             groupe_intervention = PHN.C1,
                                             variable = x)
                                         }),
                                  .SDcols="VOTED98",
                                  by=c("strates_pscore")]

#On n'a plus qu'à agréger ces effets spécifiques à chaque strate
ATE_stratification<-effet_par_strate[,
                                     list(ATE=mean(VOTED98))]
ATE_stratification

##         ATE
## 1: 0.114577

Comme la stratification ne permet pas toujours de parvenir à un équilibrage parfait des variables de conditionnement, il est courant dans la pratique empirique, plutôt que de considérer la différence entre les taux de participation dans chaque strate, d’estimer par la méthode des moindres carrés ordinaires une régression linéaire de la participation électorale sur (i) une variable dichotomique indiquant que l’on a reçu l’appel téléphonique et (ii) les variables de conditionnements incluses dans l’estimation du score de propension. On peut ensuite récupérer le coefficient portant sur la première variable dans chacune des strates et agréger ces coefficients avec des poids proportionnels à la taille de chaque strate. L’idée est que l’inclusion des variables de conditionnement doit permettre de limiter les biais dûs aux imperfections de l’équilibrage même après stratification.

#On commence par estimer la différence de taux de participation électorale
# à l'intérieur de chaque strate avec une régression linéaire
effets_par_strates_OLS<-sapply(
  X=levels(
    as.factor(
      GerberGreenImai$strates_pscore)),
  FUN=function(x){
    lm(VOTED98 ~ 
         PHN.C1 +
         PERSONS +
         WARD +
         AGE +
         MAJORPTY +
         VOTE96.0 +
         VOTE96.1 +
         NEW + 
         AGE2 +
         PERSONS*VOTE96.0 + 
         PERSONS*NEW,
       data=
         GerberGreenImai[
           strates_pscore==x])$coefficients[
             "PHN.C1"]
       })

#On n'a plus qu'à agréger ces estimations spécifiques à chaque strate
ATE_stratification_OLS<-data.table(mean(effets_par_strates_OLS))
colnames(ATE_stratification_OLS)<-c("ATE")
ATE_stratification_OLS

##          ATE
## 1: 0.1247301

5.6.2 Appariement

L’approche par appariement sur le score de propension (propensity score matching en anglais) consiste à mettre en face de chaque individu ayant reçu l’appel téléphonique incitant à voter (respectivement en face de chaque individu n’ayant pas reçu l’appel téléphonique) un individu (ou un ensemble d’individus) n’ayant pas reçu l’appel (respectivement ayant reçu l’appel) et pour lequel la valeur du score de propension est la même que pour l’individu original. En théorie, si l’on disposait des vraies valeurs du score de propension et d’un échantillon de taille infinie, on pourrait faire cette appariement de façon exacte, c’est-à-dire en exigeant que les couples d’individus soient constitués en appariant des individus ayant rigoureusement la même valeur du score de propension.

En pratique, il faut accepter de sortir de cette approche exacte, et mettre en place une forme d’extrapolation en considérant que sont appariables les individus pour lesquels les valeurs estimées du score de propension diffèrent mais sont très proches. Pour ce faire, on va souvent choisir le ou les individus de l’autre groupe dont la valeur estimée du score de propension est la plus proche de celle de l’individu de départ. C’est ce que l’on appelle appariement au plus proche voisin (nearest neighbour matching en anglais). Schématiquement, il y a quatre grandes questions à se poser pour le mettre en place :

1. Veut-on faire un appariement avec ou sans remise ? Dans le premier cas, pour chaque individu de départ, par exemple du groupe ayant reçu l’appel téléphonique, on considère comme appariables tous les individus de l’échantillon qui n’ont pas reçu l’appel téléphonique. Dans le second cas, on enlève au préalable tous les individus n’ayant pas reçu l’appel téléphonique que l’on a apparié à un individu ayant reçu l’appel : l’ordre dans lequel on fait l’appariement importe, et schématiquement plus un couple est issu d’un appariement tardif, plus l’écart des valeurs estimées du score de propension sera grand.
2. Combien d’individus souhaite-t-on apparier à chaque individu de départ ? Ce nombre peut être plus grand que 1. Faire un appariement avec un plus grand nombre d’individus peut être bénéfique pour la précision de l’estimation, mais cela peut aussi générer des biais parce que chaque individu supplémentaire aura une valeur estimée du score de propension (et donc, on l’espère si l’estimation du score de propension est de bonne qualité, une vraie valeur du score de propension) plus éloignée que celui d’avant, et sera donc moins comparable à l’individu de départ.
3. Se dote-t-on d’exigences supplémentaires sur la qualité de chaque appariement ? Pour certains individus, typiquement ceux pour lesquels le score de propension est très proche de 0 ou 1, il peut être très difficile de trouver des individus assez comparables de l’autre groupe à apparier. Pour éviter ce problème, on peut adopter deux stratégies. La première consiste à éliminer tous les individus dont les valeurs estimées du scores de propension sont trop faibles ou trop élevés avant même de commencer l’étape d’appariement ; cela revient à éliminer les individus pour lesquels ces valeurs estimées sont plus petites que 10% ou plus grande que 90%. Crump et al. (2009) proposent des règles de décision sur ces bornes davantage guidées par les données, qui sont souvent bien approximées par ce choix de 10-90. La seconde stratégie consiste à refuser les appariements entre individus pour lesquels la valeur absolue de la différence entre les valeurs estimées du scores de propension dépasse un certain seuil, appelé (en anglais) caliper. Ainsi, si pour un individu on ne trouve pas d’individu appariable suffisamment proche du point de vue des valeurs estimées du score de propension, on retire tout bonnement cet individu de l’échantillon. Ces deux stratégies ont l’intérêt de réduire les biais dûs à des appariements entre individus insuffisamment comparables. Elles ont comme défaut de changer la quantité estimée : on n’estime plus alors l’effet moyen de l’intervention dans la population d’intérêt, mais dans la population pour laquelle le score de propension prend certaines valeurs, ou pour la population appariable, ce qui peut rendre l’interprétation des résultats difficile.
4. Souhaite-t-on ajouter une étape supplémentaire pour corriger le fait que l’appariement n’est pas exact, et donc que les valeurs des variables de conditionnement ne sont pas exactement les mêmes pour l’individu de départ et l’individu qu’on lui apparie ? L’idée est de commencer par estimer séparément dans chaque groupe défini par l’intervention une régression linéaire de la variable d’intérêt sur les variables de conditionnement, et de calculer comme pseudo-effet causal individuel non plus la différence entre la valeur de la variable d’intérêt pour l’individu de départ, et celle pour l’individu qu’on lui apparie (ou la moyenne du groupe qu’on lui apparie), mais entre la valeur pour l’individu de départ, et une valeur corrigée qui prend en compte à la fois la valeur de la variable d’intérêt pour les individus qu’on apparie à l’individu de départ, et les variations de la moyenne de cette variable d’intérêt dans le groupe de ces individus lorsque l’on fait légèrement varier les variables de conditionnement (Abadie et Imbens (2011)). Cette sophistication permet d’aboutir à des estimations moins biaisées et assez précises, mais peut avoir l’inconvénient d’exiger encore une étape supplémentaire.

Le fragment de code suivant met en place cette technique d’appariement sur le score de propension aux plus proches voisins sur l’exemple emprunté à Imai (2005), pour lequel on a au préalable estimé le score de propension. On commence par utiliser cet appariement pour tester la propriété équilibrante du score de propension, puis on procède à l’estimation des effets causaux moyens du score de propension à proprement parler.

#On commence par apparier chaque individu observé à ses 5 plus proches voisins
# de l'autre groupe, avec remplacement (on n'élimine donc pas au fur et à 
# mesure les individus que l'on a réussi à apparier)
nb_match<-5

#Première étape : la petite table avec les individus de départ, la variable
# qui dit s'ils ont reçu ou non l'appel téléphonique, et la valeur estimée
# du score de propension
GerberGreenImai[,
                indiv_id:=as.character(.I)]
individus_de_depart<-GerberGreenImai[,
                                     c("indiv_id",
                                       "PHN.C1",
                                       "pscore_estimates")]

#On apparie dans un premier temps tous les individus possibles à tous les
# individus de l'autre groupe
individus_a_apparier<-individus_de_depart
individus_a_apparier[,
                     autre_groupe:=1-PHN.C1]
colnames(individus_a_apparier)[1]<-c("indiv_id_a_apparier")
appariement<-merge(individus_de_depart,
                   individus_a_apparier[,
                                        -c("PHN.C1")], 
                   by.x="PHN.C1",
                   by.y="autre_groupe",
                   allow.cartesian = TRUE)[,
                                           -c("autre_groupe")]

#On classe pour chaque individu de départ les couples potentiels dans l'ordre
# croissant de la valeur absolue de la différence des valeurs estimées du 
# score de propension
appariement[,
            abs_diff_pscore:=abs(pscore_estimates.x-
                                   pscore_estimates.y)]
setorder(appariement,
         indiv_id,
         abs_diff_pscore)

#On garde seulement pour chaque individu à apparier les 5 premières 
# propositions : ce sont les individus avec les plus petites différentes de 
# score de propension estimé
appariement[,
            rang_couple:=cumsum(PHN.C1+1-PHN.C1),
            by=indiv_id]
appariement<-appariement[rang_couple<=nb_match,
                         c("indiv_id",
                           "PHN.C1",
                           "indiv_id_a_apparier")]

#On va regarder la propriété équilibrante du score de propension avec cette
# technique d'apppariement

#On définit les variables de conditionnement sur lesquelles on va tester 
# la propriété équilibrante du score de propension 
variables_conditionnement<-c("PERSONS",
                             "AGE",
                             "MAJORPTY",
                             "VOTE96.0",
                             "VOTE96.1",
                             "NEW")

#Comme pour la stratification : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement avant l'appariement
contrastes_bruts<-GerberGreenImai[, 
                                  lapply(X=.SD,
                                         FUN=function(x){
                                           list(
                                             diff_moy(
                                               variable=x,
                                               groupe_intervention=PHN.C1),
                                             sqrt(0.5*var(x)))
                                           }),
                                  .SDcols=variables_conditionnement]
contrastes_bruts[,
                 stat:=c("diff_moy",
                         "spread")]
contrastes_bruts<-melt(contrastes_bruts,
                      variable.name="variable",
                      value.name="valeur",
                      id.vars="stat")

#Avec appariement
#Pour récupérer les différences moyennes après appariement il faut un peu
# plus de travail
#On crée une table qui stocke (1) les données des individus de départ et (2) les
# données des individus qu'on leur apparie
GerberGreenImai_matching<-rbind(GerberGreenImai,
                                merge(appariement,
                                      GerberGreenImai,
                                      by.x=c("indiv_id_a_apparier"),
                                      by.y="indiv_id"),
                                idcol="Matching",
                                fill=TRUE)
#Pour bien faire la différence entre l'appel reçu par l'individu de départ
# et celui reçu par l'éventuel individu qu'on lui apparie
GerberGreenImai_matching[,
                         c("appel_indiv_dep",
                           "appel_ego"):=list(
                             fcase(
                               Matching==1,
                               PHN.C1,
                               Matching==2,
                               PHN.C1.x),
                             fcase(
                               Matching==1,
                               PHN.C1,
                               Matching==2,
                               PHN.C1.y)
                           )]

#Quand on regarde côté apparié, chaque individu compte 1/5 (le nombre de
# couples que l'on forme pour chaque individu de départ), mais les poids valent
# toujours 1 quand on regarde côté individus de départ
GerberGreenImai_matching[,
                         poids_matching:=fcase(
                           Matching==1,
                           1,
                           Matching==2,
                           1/nb_match
                         )]

#On calcule la différence de valeur séparément pour chaque groupe 
# d'individus de départ : c'est donc la différence entre l'individu de départ
# et tous les individus appariés à lui
#Par linéarité de la moyenne, c'est pareil de considérer la différence entre
# la moyenne des "vrais" individus et la moyenne de ceux qu'on leur apparie
# en faisant bien attention à utiliser le statut de l'individu de départ
contrastes_matching_par_groupe<-
  GerberGreenImai_matching[,
                           lapply(
                             X=.SD,
                             FUN=function(x){
                               diff_moy(variable=x,
                                        groupe_intervention=
                                          appel_ego,
                                        poids=
                                          poids_matching)
                               }),
                           .SDcols=variables_conditionnement, 
                           by=c("appel_indiv_dep")
                           ]

#On fait la moyenne de ces différences standardisées avec des poids 
# proportionnels à la part dans la population de New Haven
contrastes_matching_par_groupe[,
                               poids_groupe:=
                                 fcase(
                                   appel_indiv_dep==1,
                                   mean(GerberGreenImai$PHN.C1),
                                   appel_indiv_dep==0,
                                   1-mean(GerberGreenImai$PHN.C1)
                                 )]
contrastes_agreges_matching<-
  contrastes_matching_par_groupe[,
                                 lapply(X=.SD,
                                        FUN=
                                          function(x){
                                            sum(x*poids_groupe)/
                                              sum(poids_groupe)
                                            }),
                                 .SDcols=variables_conditionnement]
contrastes_agreges_matching[,
                            stat:="diff_moy"]
contrastes_agreges_matching<-melt(contrastes_agreges_matching,
                                  id.vars="stat",
                                  variable.name="variable",
                                  value.name="valeur")

#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
#On utilise pour ça la fonction que l'on a créée pour la stratification
contrastes_matching<-contrastes_propre(contrastes_bruts,
                                       contrastes_agreges_matching)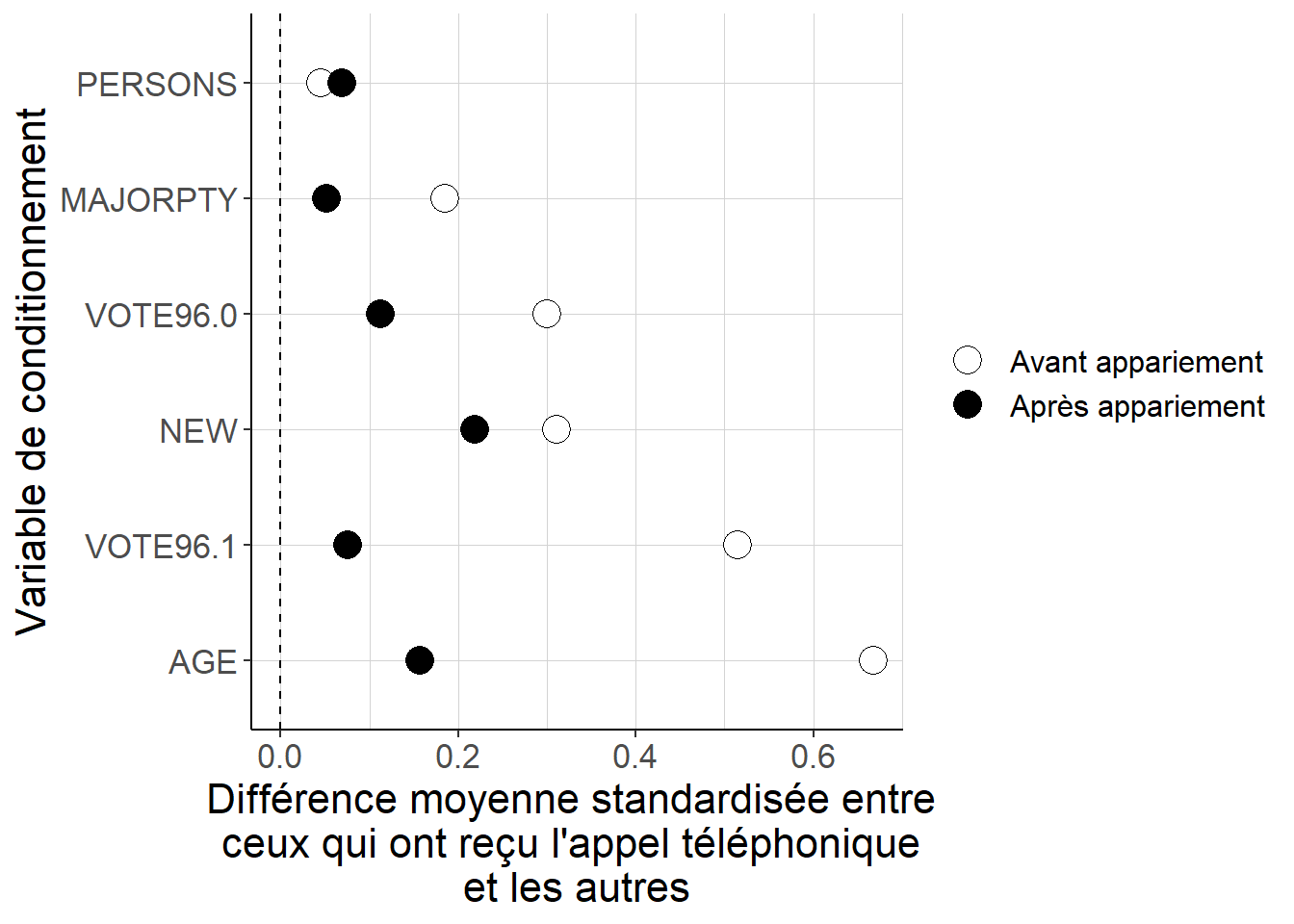

Figure 5.12: Alors que les différences quant aux valeurs des variables de conditionnement entre les individus qui ont reçu l’appel téléphonique et les autres peuvent être importantes lorsque l’on considère les données brutes, apparier chaque individu aux 5 individus de l’autre groupe défini par le fait d’avoir reçu ou non l’appel téléphonique dont les valeurs estimées du score de propension sont les plus proches de celles de l’individu de départ conduit à des différences beaucoup plus faibles. Cela suggère que la stratégie d’appariement permet de mieux équilibrer les deux groupes du point de vue de ces variables de conditionnement.

On vérifie ainsi que la stratégie d’appariement aux plus proches voisins sur le score de propension permet de réduire substantiellement les écarts du point de vue des variables de conditionnement qui existent au départ entre les individus qui ont reçu l’appel téléphonique incitant à voter et les autres, bien que dans le cas présent cette diminution ne soit pas aussi forte qu’on pourrait l’espérer : de différences non-négligeables demeurent entre les deux groupes sur certaines dimensions. Cela peut suggérer ou bien que la spécification du score de propension n’est pas tout à fait adaptée, ou bien que la trop petite taille d’échantillon contraint à apparier ensemble des individus finalement assez différents les uns des autres.

Après cette étape, on peut passer à l’estimation directe des effets causaux moyens de l’appel téléphonique sur la participation électorale. Pour ce faire, on doit comparer les individus de chaque groupe à leurs alter ego de l’autre groupe auxquels on les a appariés.

#On commence par estimer la différence de taux de participation électorale
# à l'intérieur de chaque groupe défini par l'intervention, entre les individus
# de départ et ceux auxquels on les a appariés
effet_par_groupe<-
  GerberGreenImai_matching[,
                           lapply(X=.SD,
                                  FUN=function(x){
                                    diff_moy(
                                      groupe_intervention = appel_ego,
                                      variable = x, 
                                      poids=poids_matching)
                                    }),
                           .SDcols="VOTED98",
                           by=c("appel_indiv_dep")]

#On n'a plus qu'à agréger ces effets spécifiques à chaque groupe
effet_par_groupe[,
                 poids_groupe:=
                   fcase(
                     appel_indiv_dep==1,
                     mean(GerberGreenImai$PHN.C1),
                     appel_indiv_dep==0,
                     1-mean(GerberGreenImai$PHN.C1)
                     )]
ATE_matching<-effet_par_groupe[,
                               list(ATE=sum(VOTED98*poids_groupe)/
                                      sum(poids_groupe))]
ATE_matching

##           ATE
## 1: 0.07143781

Dans le cas présent, parce que l’équilibrage n’est pas parfait après appariement, ce qui signifie qu’il existe encore des différences non-négligeables entre les deux groupes du point de vue de la distribution des caractéristiques observables définies par les variables de conditionnement, on est tenté d’utiliser la correction qui passe par une première étape de régression linéaire comme le proposent Abadie et Imbens (2011). Cette estimation est réalisée en Annexe B.4.

5.6.3 Repondération

La stratégie de repondération est justifiée par le fait que, si l’on pouvait connaître les vraies valeurs du score de propension, alors on pourrait construire un jeu des poids tel que :

1. la distribution des caractéristiques observables, à l’intérieur de chacun des groupes définis par le fait d’avoir reçu ou non l’appel téléphonique incitant à voter est la même que dans la population toute entière dés lors que l’on applique cette nouvelle pondération, et ;
2. lorsque l’on utilise ce jeu de poids, la différence des moyennes entre les deux groupes identifie les effets causaux moyens de l’intervention.

Ces poids sont inversement proportionnels à la valeur du score de propension \(p(X_i)\) pour le groupe qui a reçu l’appel téléphonique, et inversement proportionnel à son complément \(1-p(X_i)\) dans l’autre groupe. En d’autres termes, ces poids vont donner beaucoup d’importance aux individus qui ont reçu un appel alors que cela était peu probable, et à ceux qui n’ont pas reçu d’appel alors que cela était probable, et moins d’importance à ceux dont la situation était assez probable au regard de leurs caractéristiques observables.

La principale difficulté de l’usage de cette technique de repondération tient à ce qu’en définissant ces poids à partir de l’inverse du (complément du) score de propension, on est conduit à donner une très grande importance dans l’estimation à certains individus, typiquement ceux qui ont reçu un appel alors que cela était très improbable. En donnant ainsi une importante démesurée à certains individus, on risque de générer beaucoup d’instabilité dans l’estimation.

Pour se prémunir contre ce risque, on peut suivre deux pistes. La première est de normaliser les poids. En effet, on sait que si l’on pouvait utiliser les vraies valeurs du score de propension, alors la moyenne des poids dans chacun des deux groupes serait égale à 1. Comme en pratique on ne peut utiliser que les valeurs estimées du score de propension, cela n’est pas assuré a priori. Ainsi, alors que la référence aux vraies valeurs du score de propension suggère que l’on peut se passer de mettre les poids au dénominateur lorsque l’on calcule les moyennes (voir A.15), le faire peut conduire à une estimation plus stable lorsque l’on se fonde sur les valeurs estimées du score de propension.

Une deuxième piste, lorsque la première continue à conduire à des estimations instables, est comme cela a été discuté pour le cas de l’appariement, d’éliminer de l’estimation les individus pour lesquels le score de propension est trop proche de 0 ou 1. Cela améliore la précise de l’estimation parce que l’on retire ainsi des individus qui peuvent générer de grandes fluctuations dans l’estimation. Cela étant, ce faisant on change aussi la quantité estimée, qui ne correspond plus aux effets causaux moyens de l’intervention dans toute la population, mais à ces effets moyens dans une sous-population qu’il peut être difficile de définir précisément et qui dépend potentiellement du choix de spécification retenue pour le score de propension.

Le fragment de code suivant met en application cette technique de repondération sur l’exemple emprunté à Gerber et Green (2000) et Imai (2005). Comme pour les deux stratégies précédentes, on a déjà estimé le score de propension ; on commence par mettre à l’épreuve sa propriété équilibrante, puis on passe à l’estimation à proprement parler.

#On va calculer les poids à partir du score de propension
GerberGreenImai[,
                poids_pscore:=
                  fcase(
                    PHN.C1==1,
                    mean(GerberGreenImai$PHN.C1)/
                      pscore_estimates,
                    PHN.C1==0,
                    mean(1-GerberGreenImai$PHN.C1)/
                      (1-pscore_estimates)
                  )]

#Avec ces nouveaux poids, on va comparer du point de vue de la valeur
# des variables de conditionnement les individus selon qu'ils ont ou qu'ils 
# n'ont pas reçu un appel téléphonique

#On applique la fonction diff_moy aux variables de conditionnement, d'abord sans 
# repondération, puis avec les nouveaux poids

#On définit les variables de conditionnement sur lesquelles on va tester 
# la propriété équilibrante du score de propension 
variables_conditionnement<-c("PERSONS",
                             "AGE",
                             "MAJORPTY",
                             "VOTE96.0",
                             "VOTE96.1",
                             "NEW")

#Sans repondération : on calcule simplement la différence moyenne
# pour toutes les variables de conditionnement
contrastes_bruts<-GerberGreenImai[, 
                                  lapply(X=.SD,
                                         FUN=function(x){
                                           list(
                                             diff_moy(
                                               variable=x,
                                               groupe_intervention=PHN.C1),
                                             sqrt(0.5*var(x)))
                                           }),
                                  .SDcols=variables_conditionnement]
contrastes_bruts[,
                 stat:=c("diff_moy",
                         "spread")]
contrastes_bruts<-melt(contrastes_bruts,
                      variable.name="variable",
                      value.name="valeur",
                      id.vars="stat")

#Avec repondération
contrastes_agreges_reponderation<-
  GerberGreenImai[, 
                  lapply(
                    X=.SD,
                    FUN=function(x){
                      diff_moy(variable=x,
                               groupe_intervention=
                                 PHN.C1, 
                               poids=poids_pscore)
                      }),
                  .SDcols=variables_conditionnement]
contrastes_agreges_reponderation[,
                                 stat:="diff_moy"]
contrastes_agreges_reponderation<-
  melt(contrastes_agreges_reponderation,
       id.vars="stat",
       value.name="valeur",
       variable.name="variable")

#On n'a plus qu'à tout mettre dans une seule table puis à diviser les écarts
# de moyennes par la dispersion
#On utilise pour ça la fonction que l'on a créée pour la stratification
contrastes_reponderation<-
  contrastes_propre(contrastes_bruts,
                    contrastes_agreges_reponderation)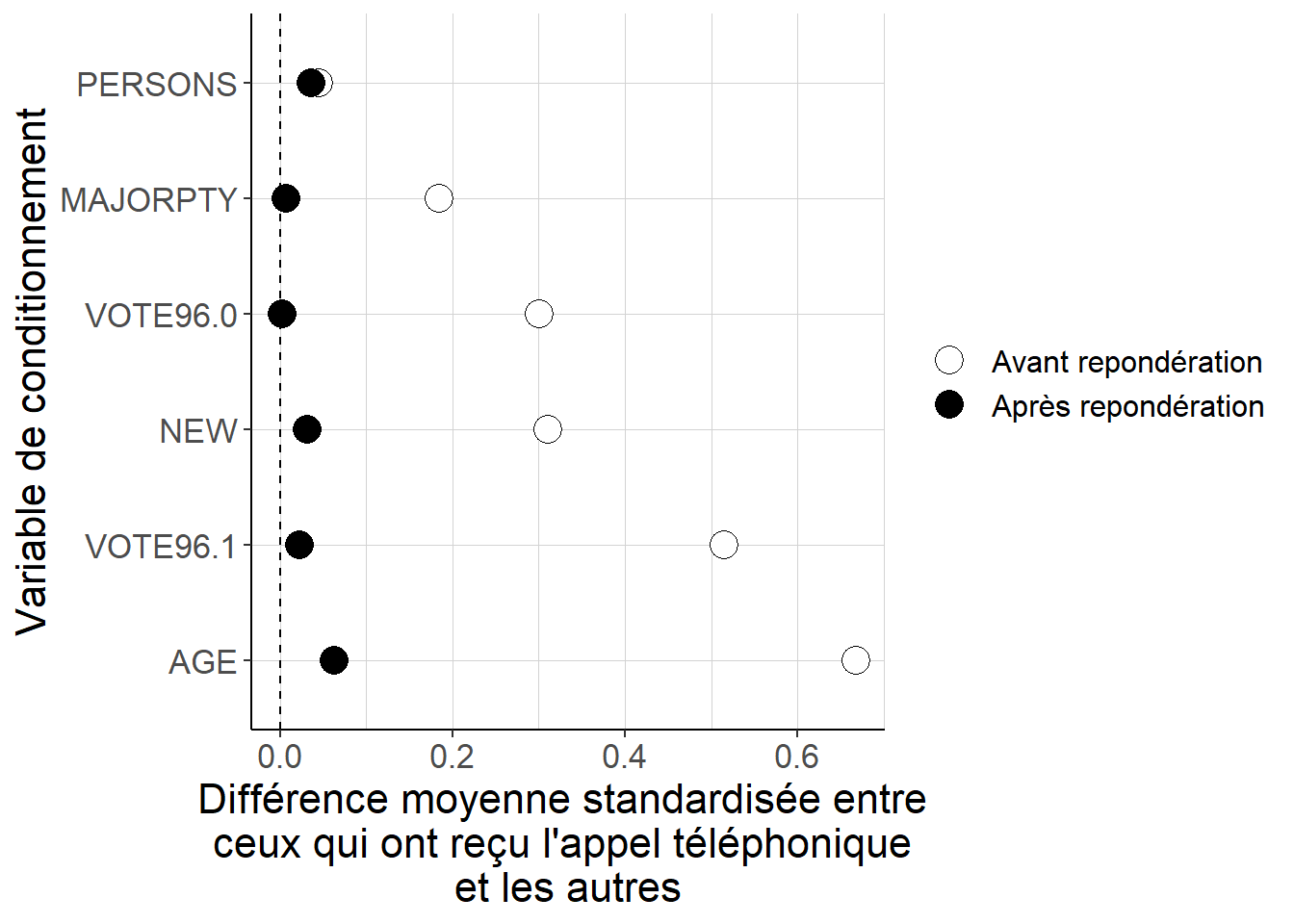

Figure 5.13: Alors que dans les données brutes, les deux groupes définis par le fait d’avoir ou non reçu un appel téléphonique incitant à voter sont assez différents du point de vue de leurs caractéristiques observables, la repondération permet de réduire considérablement ces différences. En d’autres termes, utiliser ces poids permet de s’approcher d’une situation où les deux groupes sont équilibrés en termes de la distribution des caractéristiques observables décrites par les variables de conditionnement.

En utilisant les poids définis à partir du score de propension, on parvient à s’approcher de façon convaincante de la situation où le score de propension permet d’équilibrer les deux groupes définis par l’intervention au regard de leurs caractéristiques observables. Il faut noter que l’on a utilisé ici les poids normalisés. On peut ensuite s’intéresser à l’estimation des effets causaux moyens de cette intervention sur la participation électorale, et comparer sur cet exemple les résultats obtenus à partir des deux jeux de poids, normalisés ou non.

#Estimation de l'ATE avec les poids non-normalisés
ATE_reponderation_nonnorm<-
  GerberGreenImai[,
                  list(ATE=
                         sum(poids_pscore*PHN.C1*VOTED98)/
                         sum(PHN.C1)-
                         sum(poids_pscore*(1-PHN.C1)*VOTED98)/
                         sum(1-PHN.C1))]
ATE_reponderation_nonnorm

##           ATE
## 1: 0.09615629

#Estimation de l'ATE avec les poids normalisés
ATE_reponderation_norm<-
  GerberGreenImai[,
                  list(ATE=
                         sum(poids_pscore*PHN.C1*VOTED98)/
                         sum(poids_pscore*PHN.C1)-
                         sum(poids_pscore*(1-PHN.C1)*VOTED98)/
                         sum(poids_pscore*(1-PHN.C1)))]
ATE_reponderation_norm

##          ATE
## 1: 0.1113282

5.6.4 Ces estimations sont-elles robustes ?

Une fois ces estimations réalisées, on peut légitimement se demander si elles conduisent à des résultats similaires ou pas. En effet, toutes ces techniques supposent un nombre important d’étapes pour lesquelles il n’existe pas de solution évidente, et qui laissent donc la main à la personne qui fait l’estimation quant au choix qu’elle retient : fonction de lien et spécification du score de propension, choix d’une technique plutôt qu’une autre, choix du nombre de strates, choix du nombre d’individus à apparier, appariement avec ou sans remise, normalisation des poids etc. La qualité d’une estimation tient donc d’une part à la qualité des hypothèses théoriques d’identification – indépendance conditionnelle et support commun –, mais aussi à ce que l’estimation dépend le moins possible de ces choix difficiles à contrôler. Il est donc de bonne politique de vérifier que de petites modifications dans l’implémentation de l’estimation ne conduisent pas à des résultats fondamentalement différents.

La figure 5.14 propose de comparer toutes les estimations réalisées du point de vue de leurs résultats. De façon rassurante, ces résultats ne diffèrent pas de façon trop importante selon la technique d’estimation retenue, à part peut-être pour la technique d’appariement dont on a vu que sur cet exemple, elle ne permettait pas d’assurer un très bon équilibrage des variables de conditionnement. Cela étant, les divergences ne sont pas non plus très importantes. Un point important ici est qu’une divergence importante entre plusieurs approches ne jette pas ici le doute sur la seule estimation divergente par rapport aux autres, mais bel et bien sur toutes les estimations : leur première qualité doit être la robustesse, et donc leur faible dépendance vis-à-vis des choix potentiellement incontrôlés retenus par la personne qui conduit l’évaluation.

Figure 5.14: Lorsque l’on compare les différentes approches, fondées sur des valeurs du score de propension estimées à partir d’un modèle logit, on récupère des estimations relativement proches des effets causaux moyens de l’appel téléphonique incitant à voter sur la participation électorale. Seul l’approche par appariement sur le score de propension semble un peu diverger des autres approches, sans toutefois conduire à des résultats très différents à première vue. Cela peut tenir au fait que l’équilibrage semble moins bien assuré par l’appariement que par la stratification ou la repondération. Il faudrait quoi qu’il en soit encore évaluer la précision de ces estimations pour savoir si ces divergences sont réelles ou reflètent seulement des fluctuations aléatoires liées à l’échantillonage et à l’assignation aléatoire à l’intervention.