2.6 Comparaisons avec l’espérance conditionnelle
Cette section propose plusieurs comparaisons entre les coefficients issus de la régression linéaire par les moindres carrés ordinaires et le concept d’espérance conditionnelle. La lectrice ou lecteur désireux de se remettre en mémoire au préalable les principales propriétés de l’espérance conditionnelle est invité à se rendre en 1.3.3. Pour la bonne compréhension de cette section, il est suffisant de se souvenir que l’espérance conditionnelle, notée \(\mathbb{E}[Y \mid X=x]\) s’interprète essentiellement comme la moyenne de la variable \(Y\) pour le groupe des individus pour lesquels la valeur de la variable \(X\) est égale à \(x\).
2.6.1 La régression linéaire par les moindres carrés ordinaires ne dépend que de l’espérance conditionnelle
Lorsque l’on considère, au sein de la population des salariés étatsuniens, la régression linéaire du salaire horaire (en $ par heure) sur le niveau d’éducation en années, les coefficients contiennent-t-ils une autre information que le salaire moyen pour chaque niveau d’éducation ? La réponse est négative. En effet, pour ce qui concerne la valeur des coefficients, il revient exactement au même de (i) régresser le salaire horaire sur l’éducation, ou (ii) attribuer à chaque individu le salaire moyen pour son niveau d’éducation, puis régresser ce salaire moyen sur le niveau d’éducation9.
Le fragment de code suivant permet de vérifier ce fait à partir des données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On crée une variable égale à la moyenne du salaire pour chaque niveau d'éducation
mean_wage_educ<-CPS[,
list(mean_wage=mean(wage)),
by="education"]
CPS<-merge(CPS,
mean_wage_educ,
by=c("education"))
#On estime la régression du salaire horaire sur l'éducation
reg_wage_educ<-lm(wage~education,
data=CPS)
reg_wage_educ##
## Call:
## lm(formula = wage ~ education, data = CPS)
##
## Coefficients:
## (Intercept) education
## -0.7460 0.7505#On estime la régression de la moyenne conditionnelle du salaire horaire sur
# l'éducation
reg_wage_mean_educ<-lm(mean_wage~education,
data=CPS)
reg_wage_mean_educ##
## Call:
## lm(formula = mean_wage ~ education, data = CPS)
##
## Coefficients:
## (Intercept) education
## -0.7460 0.7505#On vérifie que les deux jeux de coefficients sont bien égaux
all.equal(reg_wage_educ$coefficients,
reg_wage_mean_educ$coefficients)## [1] TRUE#On rajoute juste un peu de bruit à la variable d'éducation pour faciliter la
# visualisation quand il y a plusieurs salariés avec le même niveau
# d'éducation
CPS$jitter_education<-
CPS$education+
(table(CPS$education)[as.character(CPS$education)]>1)*
rnorm(nrow(CPS),sd=0.3)
#Commun aux deux panneaux : la droite de régression et la mise en forme
reg_line<-ggplot(data=CPS,
aes(x=jitter_education))+
geom_line(color="red",
linewidth=3,
aes(x=jitter_education,
y=reg_wage_educ$coefficients["(Intercept)"]+
reg_wage_educ$coefficients["education"]*
jitter_education))+
theme_classic()+
coord_cartesian(ylim=c(-5,30))+
xlab("Années d'éducation")+
theme(text=element_text(size=32),
strip.text.x = element_text(size=32),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))
#Visualisation du nuage de points pour la régression du salaire
reg_line+
geom_point(color="black",
alpha=0.2,
size=5,
aes(y=wage))+
ylab("Salaire horaire ($ par heure)")
#Visualisation du nuage de points pour la régression du salaire moyen par niveau
# d'éducation
reg_line+
geom_point(aes(x=education,
y=mean_wage),
color="black",
linewidth=5,
alpha=0.2)+
ylab("Salaire horaire moyen ($ par heure)")## Warning in geom_point(aes(x = education, y = mean_wage), color = "black", :
## Ignoring unknown parameters: `linewidth`
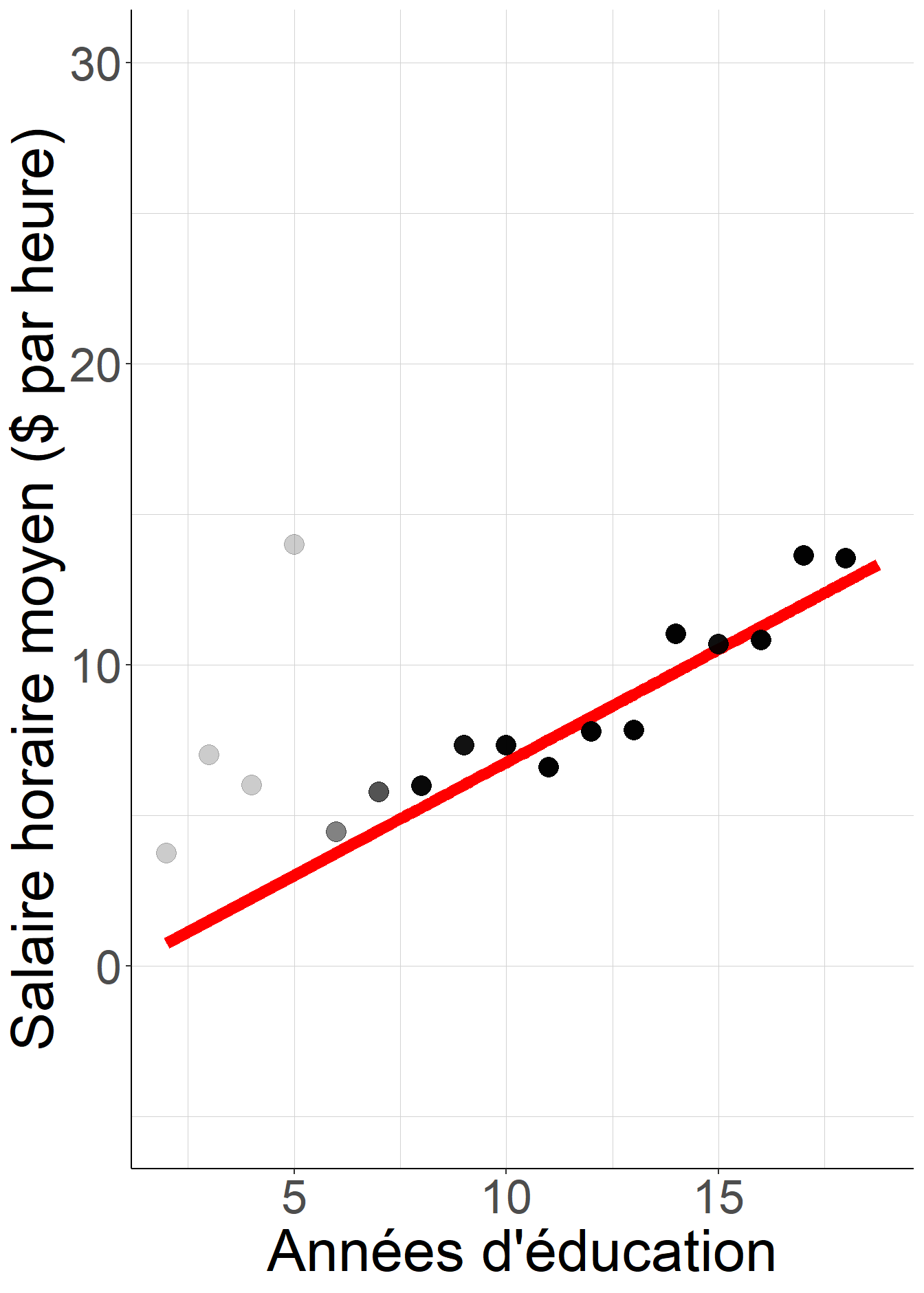
Figure 2.5: La pente et l’ordonnée à l’origine de la droite de régression restent exactement la même si on remplace pour chaque individu son salaire par le salaire moyen des individus ayant le même niveau d’éducation.
Ce résultat est une fois encore bien plus général que ce seul exemple empirique. Ainsi, les coefficients obtenus par la méthode des moindres carrés ordinaires ne dépendent que de l’espérance conditionnelle de \(Y\) sachant \(X\) et de la distribution des variables indépendantes \(X\)10.
En fait, régression linéaire et espérance conditionnelle entretiennent des liens plus profonds : l’espérance conditionnelle peut s’interpréter comme une solution du problème des moindres carrés ordinaires dans un ensemble plus général que celui des seules fonctions affines, ce qui explique pourquoi raisonner en termes de régression linéaire, ou en termes de moyennes de la variable dépendante dans des groupes définis par les valeurs prises par les variables indépendantes revient souvent pratiquement au même. L’Annexe B.1 examine ce fait de plus près.
Avertissement
L’exemple précédent fonctionne dans la mesure où on a gardé chaque observation individuelle et on lui a assigne comme variable dépendante le salaire moyen de son niveau d’éducation. Si on voulait partir plutôt de données agrégées par niveau d’éducation, il faudrait penser à pondérer chaque groupe d’éducation par sa taille dans la population.
L’Annexe B.2 prolonge ces résultats en examinant les liens entre le coefficient de la régression linéaire par la méthode des moindres carrés ordinaires et les variations locales du salaire moyen entre niveaux d’éducation distants d’une année, c’est-à-dire les quantités de la forme \(\mathbb{E}[Y \mid X=x+1]- \mathbb{E}[Y \mid X=x]\). Elle établit que le coefficient de l’éducation dans la régression précédente peut s’interpréter comme une moyenne pondérée de telles quantités.
2.6.2 La régression linéaire par les moindres carrés ordinaires et l’espérance conditionnelle coïncident pour la régression saturée
2.6.2.1 Retrouver l’espérance conditionnelle à l’aide de la régression saturée
La méthode des moindres carrés peut parfois être utilisée pour mesurer des valeurs moyennes par groupe. Ainsi, lorsque l’on s’intéresse à la population des salariés étatsuniens, si l’on régresse le salaire horaire sur quatre variables dichotomiques codant l’appartenance à un groupe défini par l’intersection d’une classe de sexe et d’un niveau d’éducation, et que l’on omet la constante pour se tenir à distance des problèmes de colinéarité, alors les coefficients obtenus sont égaux au salaire moyen à l’intérieur de chacun de ces groupes.
Le fragment de code suivant permet d’illustrer ce fait à partir des données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On crée des variables représentant l'intersection d'un sexe et d'un niveau
# d'éducation scolaire
CPS$women_college<-as.numeric(CPS$gender=="female"
& CPS$education>=16)
CPS$men_college<-as.numeric(CPS$gender=="male"
& CPS$education>=16)
CPS$women_noncollege<-as.numeric(CPS$gender=="female"
& CPS$education<16)
CPS$men_noncollege<-as.numeric(CPS$gender=="male"
& CPS$education<16)
#On crée aussi les variables représentant les sexes et le niveau d'éducation
# scolaire
CPS$college<-as.numeric(CPS$education>=16)
CPS$female<-as.numeric(CPS$gender=="female")
#On régresse le salaire sur ces 4 indicatrices (en omettant la constante)
reg_sat<-lm(wage~women_college + women_noncollege + men_college + men_noncollege -1,
data=CPS)
reg_sat##
## Call:
## lm(formula = wage ~ women_college + women_noncollege + men_college +
## men_noncollege - 1, data = CPS)
##
## Coefficients:
## women_college women_noncollege men_college men_noncollege
## 10.998 6.933 12.868 9.094#On compare les coefficients avec les salaires moyens à l'intérieur de chaque groupe
all.equal(as.numeric(reg_sat$coefficients["women_college"]),
mean(CPS[women_college==1]$wage))## [1] TRUEall.equal(as.numeric(reg_sat$coefficients["women_noncollege"]),
mean(CPS[women_noncollege==1]$wage))## [1] TRUEall.equal(as.numeric(reg_sat$coefficients["men_college"]),
mean(CPS[men_college==1]$wage))## [1] TRUEall.equal(as.numeric(reg_sat$coefficients["men_noncollege"]),
mean(CPS[men_noncollege==1]$wage))## [1] TRUECe résultat a une valeur plus générale : on dit que l’espérance conditionnelle et les coefficients obtenus par la méthode des moindres carrés ordinaires coïncident dans le cas de la régression saturée.
À retenir
Si les variables indépendantes sont exclusivement des variables indicatrices dichotomiques telles que (i) les différents groupes délimités par chacune de ces variables recouvrent toute la population d’intérêt et (ii) il n’est pas possible d’appartenir simultanément à plusieurs de ces groupes, alors les coefficients de la régression linéaire par les moindres carrés ordinaires sont égaux à l’espérance conditionnelle de la variable dépendante dans chacun de ces groupes.
Formellement, il s’agit donc de régresser la variable aléatoire \(Y\) sur des variables indicatrices dichotomiques qui correspondent au découpage de la population d’intérêt en \(d\) ensembles disjoints, en omettant la constante pour éviter la colinéarité : \(Y = \sum_{i=1}^d \beta_i X_i + \epsilon\). La proposition précédente revient à dire que \(\beta_i = \mathbb{E}[Y \mid X_i=1]\). La preuve de cette affirmation est détaillée en A.8.
Bien entendu, compte-tenu du problème de colinéarité, on pourrait choisir d’inclure la constante et éliminer l’indicatrice d’appartenance à un sous-ensemble du lot des variables indépendantes sans changer fondamentalement le résultat : la constante serait alors égale à l’espérance conditionnelle de la variable aléatoire \(Y\) sachant que l’on se trouve dans le sous-ensemble omis, et les coefficients sur les variables indicatrices seraient égales à la différence entre l’espérance conditionnelle dans chaque sous-ensemble et l’espérance conditionnelle dans le sous-ensemble de référence.
2.6.2.2 Définir des groupes par des interactions
La régression saturée n’est pas toujours encodée sous la forme directe de \(d\) variables indicatrices correspondant au découpage de la population d’intérêt en autant de sous-ensembles. On peut aussi y parvenir au moyen d’interactions. Par exemple, si on considère la population des salariés étatsuniens, on peut penser à la répartir d’une part entre femmes et hommes (au sens de l’état-civil), et d’autre part les individus diplômés de l’enseignement supérieur et ceux qui ne le sont pas : on a ainsi deux façons différentes de découper la population d’intérêt en deux sous-ensembles disjoints. Ces deux découpages peuvent également générer un découpage en 4 sous-ensembles disjoints, si on considère les intersections de tous ces sous-ensembles. Dans une régression, on pourrait faire apparaître ces nouveaux sous-ensembles directement en créant 4 nouvelles variables indicatrices dichotomiques.
On pourrait tout aussi bien choisir une approche différente, en considérant des interactions, c’est-à-dire de nouvelles variables créées en multipliant ces variables entre elles. Par exemple, si \(X_f\) est l’indicatrice d’être une femme, et \(X_s\) l’indicatrice d’être diplômé de l’enseignement supérieur, alors la variable aléatoire \(X_fX_s\) est égale à 1 si l’individu considéré est une femme diplômée de l’enseignement supérieur, et 0 sinon. Si l’on se restreint aux salariés, et si \(Y\) désigne par exemple le salaire, on pourrait songer à estimer \(Y = \alpha + \beta X_f + \gamma X_s + \delta X_f X_d + \epsilon\). On a bien 4 coefficients à estimer, soit autant que de sous-ensembles.
La difficulté est de réussir à bien interpréter chacun d’entre eux. Ici la constante \(\alpha\) est égale à l’espérance du salaire chez les hommes non-diplômés de l’enseignement supérieur. Le coefficient \(\beta\) est égal à la différence entre l’espérance du salaire chez les femmes non-diplômées et celle chez les hommes non-diplômés. Le coefficient \(\gamma\) est égal à la différence entre l’espérance du salaire chez les hommes diplômés et l’espérance du salaire chez les hommes non-diplômés. Enfin, \(\delta\) correspond à la différence entre l’espérance du salaire chez les femmes diplômées et l’espérance du salaire des femmes non-diplômées, à laquelle on retranche la différence entre l’espérance du salaire chez les hommes diplômés et l’espérance du salaire chez les hommes non-diplômés.
Le fragment de code suivant permet de reprendre la discussion précédente dans le cas des données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On crée aussi les variables représentant les sexes et le niveau d'éducation
# scolaire
CPS$college<-as.numeric(CPS$education>=16)
CPS$female<-as.numeric(CPS$gender=="female")
#On peut comparer avec une régression spécifiée en interagissant les variables
reg_interact<-lm(wage~college + female + college*female,
data=CPS)
reg_interact##
## Call:
## lm(formula = wage ~ college + female + college * female, data = CPS)
##
## Coefficients:
## (Intercept) college female college:female
## 9.0940 3.7736 -2.1608 0.2914#On vérifie que la constante est égale au salaire moyen des hommes non-diplômés
all.equal(as.numeric(reg_interact$coefficients["(Intercept)"]),
mean(CPS[gender=="male"
& college==0]$wage))## [1] TRUE#Le coefficient sur la variable college est égal à la différence entre le salaire
# moyen des hommes diplômés et non-diplômés
all.equal(as.numeric(reg_interact$coefficients["college"]),
mean(CPS[gender=="male"
& college==1]$wage)-
mean(CPS[gender=="male"
& college==0]$wage))## [1] TRUE#Le coefficient sur la variable female est égal à la différence entre le salaire
# moyen des femmes non-diplômées et le salaire moyen des hommes non-diplômés
all.equal(as.numeric(reg_interact$coefficients["female"]),
mean(CPS[gender=="female"
& college==0]$wage)-
mean(CPS[gender=="male"
& college==0]$wage))## [1] TRUE#Le coefficient sur le terme college*female est la différence entre le salaire
# moyen des femmes diplômées et non-diplômées, moins la différence entre le
# salaire moyen des hommes diplômés et non-diplômés
all.equal(as.numeric(reg_interact$coefficients["college:female"]),
(mean(CPS[gender=="female"
& college==1]$wage)-
mean(CPS[gender=="female"
& college==0]$wage))-
(mean(CPS[gender=="male"
& college==1]$wage)-
mean(CPS[gender=="male"
& college==0]$wage)))## [1] TRUE2.6.3 La régression linéaire par les moindre carrés ordinaires permet d’agréger les contrastes conditionnels
Considérons, dans la population des salariés étatsuniens, la régression linéaire du salaire horaire sur (i) une indicatrice d’être une femme et (ii) un grand nombre d’indicatrices correspondant chacune à une modalité d’une nomenclature de professions. Ce type de régression est parfois mis en œuvre dans la littérature consacrée aux inégalités de genre sur le marché du travail en ce qu’il permettrait de comparer la rémunération des femmes et des hommes en neutralisant les effets de la ségrégation professionnelle.
En effet, il est possible de montrer que le coefficient qui porte sur la variable indicatrice d’être une femme est, dans ce cas, égal à la moyenne des écarts de salaire moyen entre femmes et hommes à l’intérieur de chaque profession de la nomenclature considérée, en mettant davantage de poids sur les professions les plus nombreuses, et sur celles où la part de femmes est proche de 50%.
Le fragment de code suivant permet de mettre en évidence le résultat précédent à partir des données du Current Population Survey.
library(AER,
quietly=TRUE)
library(data.table,
quietly=TRUE)
library(ggplot2,
quietly=TRUE)
#On charge dans un premier temps les données du CPS 1985
data("CPS1985")
CPS<-data.table(CPS1985)
#On crée deux variables dichotomiques indiquant le sexe déclaré dans
#l'enquête
CPS[,
c("female",
"male"):=list(as.numeric(gender=="female"),
as.numeric(gender=="male"))]
#On régresse le salaire sur l'indicatrice d'être une femme et l'occupation (une
# sorte d'analogue de la CS)
reg_wage_gender_occupation<-lm(wage~female + occupation,
data=CPS)
reg_wage_gender_occupation##
## Call:
## lm(formula = wage ~ female + occupation, data = CPS)
##
## Coefficients:
## (Intercept) female occupationtechnical
## 8.8204 -2.0484 4.1415
## occupationservices occupationoffice occupationsales
## -1.0736 0.2071 -0.3114
## occupationmanagement
## 4.6657#On calcule pour chaque occupation :
# 1. sa taille dans la population
# 2. la part de femmes dans cette occupation
# 3. l'écart de salaire moyen entre femmes et hommes dans cette occupation
aggreg_CPS_occupation<-CPS[,
list(size=.N,
share_female=sum(female)/sum(female+male),
var_female=sum(female)/sum(female+male)*
(1-sum(female)/sum(female+male)),
gender_gap=sum(female*wage)/sum(female)-
sum((male)*wage)/sum(male)),
by="occupation"]
#On agrège les écarts de salaire dans chaque occupation en un seul écart moyen
# avec des poids proportionnels à la taille de chaque occupation et à la variance
# var_female = part de femmes * (1- part de femmes)
aggreg_gender_gap<-aggreg_CPS_occupation[,
(aggreg_gender_gap=
sum(size*var_female*gender_gap)/
sum(size*var_female))]
aggreg_gender_gap## [1] -2.048358#On compare finalement cette quantité au coefficient de la régression linéaire
all.equal(aggreg_gender_gap,
as.numeric(reg_wage_gender_occupation$coefficients["female"]))## [1] TRUE#Une façon de visualiser ça
ggplot(data=aggreg_CPS_occupation,
aes(x=share_female,
y=gender_gap,
label=occupation,
size=size/nrow(CPS)))+
geom_point(alpha=0.5)+
geom_text(hjust=-0.125, vjust=-0.5,
size=5)+
scale_size(name="Part dans la \npopulation active \noccupée",
labels=scales::percent)+
scale_x_continuous(labels=scales::percent)+
coord_cartesian(xlim=c(0.15,0.95),
ylim=c(-4.5,0.5))+
theme_classic()+#supprime l'arrière-plan gris par défaut
ylab("Ecart de salaire horaire moyen \nentre femmes et hommes \ndans l'occupation ($ par heure)")+
#titre des axes
xlab("Part de femmes dans l'occupation")+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))+
geom_hline(color="red",
linewidth=3,
yintercept=reg_wage_gender_occupation$coefficients["female"])
Figure 2.6: Le coefficient sur la variable de sexe dans la régression linéaire du salaire horaire sur le sexe et sur les indicatrices d’occupation, représenté par l’ordonnée de la droite horizontale rouge, renvoie une moyenne pondérée d’écarts de salaire horaire entre femmes et hommes spécifiques à chaque occupation, représentés l’ordonnée de chacun des points, avec des poids qui donnent davantage d’importance (i) aux occupations les plus nombreuses dans la population et (ii) à celles dans lesquelles la part de femmes est plus proche de 50%.
Il s’agit là une fois encore d’un résultat d’une portée plus générale.
À retenir
Lorsque l’on régresse par les moindre carrés ordinaires une variable aléatoire \(Y\) sur (i) une variable dichotomique \(D\) et (ii) un lot de variables dichotomiques \(X_i\) qui découpent la population d’intérêt en autant de sous-ensembles disjoints, le coefficient sur la variable \(D\) est égal à la moyenne des contrastes conditionnels \(\mathbb{E}[Y \mid D=1,\, X_i=1] - \mathbb{E}[Y \mid D=0,\, X_i=1]\) avec des poids qui donnent davantage d’importance (i) aux groupes les plus nombreux dans la population d’intérêt et (ii) aux groupes au sein desquels la probabilité \(\mathbb{P}(D=1 \mid X_i=1)\) est plus proche de \(\frac{1}{2}\).
Formellement, cette affirmation dit que le coefficient sur la variable \(D\) serait égal à la moyenne des contrastes \(\mathbb{E}[Y \mid D=1,\, X_i=1] - \mathbb{E}[Y \mid D=0,\, X_i=1]\) avec des poids proportionnels à (i) la part de chaque groupe dans la population d’intérêt \(\mathbb{E}[X_i]\) et (ii) la variance de \(D\) à l’intérieur de chaque strate \(\mathbb{E}[D \mid X_i=1]\{1-\mathbb{E}[D \mid X_i=1]\}\). Une démonstration en est proposée en Annexe A.9.
Cette proposition est vraie pour ce qui concerne la valeur des coefficients. Elle n’est pas vraie lorsqu’il est question de l’incertitude sur ces coefficients, qui n’est abordée qu’en 2.9.↩︎
La lectrice ou le lecteur intéressé par une preuve plus formelle vérifiera que ce résultat se déduit de ce que les coefficients de la régression linéaire ne dépendent que de la covariance de la variable dépendante avec chacune des variables indépendantes, et de la matrice de variance-covariance des variables indépendantes.↩︎