4.3 Appuyer graphiquement l’hypothèse d’indépendance conditionnelle
Dans tout ce qui précède, la possibilité d’identifier les effets causaux moyens d’une intervention tient à ce que la situation empirique est traitée comme si elle résultait d’une expérience aléatoire stratifiée. En effet, c’est fondamentalement le postulat selon lequel la situation empirique est assimilable à une telle expérience qui justifie l’hypothèse qu’à l’intérieur d’une strate définie par la valeur prises par les variables observables, la comparaison des individus qui ont fait l’objet de l’intervention avec leurs homologues qui n’ont pas fait l’objet de cette intervention apporte de l’information sur les effets causaux de l’intervention.
Bien entendu, en pratique de telles expériences stratifiées sont rares, et tout tient donc à la possibilité de faire comme si la situation étudiée pouvait y être assimilée. À première vue, il n’est pas évident de déterminer dans quels cas cette hypothèse est défendable, et dans quels cas elle n’est absolument pas crédible. En particulier, on sent bien que la crédibilité de cette hypothèse tient à la délimitation des strates à l’intérieur desquelles la comparaison des individus ayant fait l’objet de l’intervention et de ceux qui n’ont pas fait l’objet de l’intervention est faite. En d’autres termes, tout dépend du choix des variables observables dont les valeurs délimitent les strates.
Ce choix est rarement commenté de façon approfondie dans la littérature. Beaucoup d’auteurs procèdent ainsi de façon heuristique, sans nécessairement consacrer un espace très important à ce choix. L’objet de cette section est au contraire de proposer une approche algorithmique pour faire ce choix, fondée sur un formalisme graphique.
4.3.1 Représentation graphique de la causalité
4.3.1.1 Grammaire élémentaire
Bien que les représentations graphiques de la causalité soient plus anciennes, une part importante de l’sage contemporain de ces méthodes est liée aux travaux de Judeas Pearl ; un aperçu détaillé de ses contributions est disponible dans Pearl (2009), qui est toutefois d’une lecture un peu fastidieuse. Un ouvrage plus accessible sur ces approches est Glymour, Pearl et Jewell (2016), et l’on en trouve une présentation dans Morgan et Winship (2014), Cunningham (2021), Huntington-Klein (2021). L’objectif poursuivi ici est de donner à la lectrice et au lecteur l’intuition des principales idées directrice des ces approches, ainsi qu’un aperçu de leur usage pratique à l’aide du package ggdag.
Dans leur article récent consacré aux effets de l’austérité économique sur les dépenses de santé publique, Jacques et Noël (2022) s’appuient sur une représentation graphique de la causalité pour motiver leur approche empirique. Plus précisément, ils proposent un graphique à cinq nœuds :
- le premier est noté “Austérité” ;
- les deuxièmes, troisièmes et quatrièmes nœuds sont étiquettés “Appartenance partisane du gouvernement”, “Organisation du système de santé”, “Conditions économiques et démographiques” ;
- le cinquième nœud est noté “Niveau et structure de la dépense de santé publique”.
Ces nœuds sont reliés entre eux par sept flèches. Ces flèches sont uni-directionnelles et représentent le flot de causalité. Ainsi, une flèche qui part de l’austérité et aboutit à la dépense de santé publique signifie que qu’une austérité plus ou moins prononcée en matière de finances publiques a des conséquences sur la dépense de santé publique, mais que l’inverse n’est pas vrai.
Le fragment de code suivant fait apparaître ces nœuds et ces flèches en utilisant le package ggdag.
library(ggdag)
library(ggplot2)
library(viridis)
graph_jacques<-dagify(SantePub~Austerite+AppartParti+SystemeSante+ConditEco,
#Pour chaque nœuds auquel aboutit au moins une flèche,
# on recense d'où partent toutes ces flèches
Austerite~AppartParti+SystemeSante+ConditEco,
exposure = "Austerite",
#La variable qui correspond à l'intervention dont on
# souhaite étudier les effets
outcome = "SantePub",
#La variable qui correspond aux conséquences que l'on
# voudrait pouvoir mesurer
labels = c("SantePub"="Santé publique",
"Austerite"="Austérité",
"AppartParti"="Appartenance \npartisane",
"SystemeSante"="Système de \nsanté",
"ConditEco"="Conditions \néconomiques"))
#Des labels pour rendre les choses plus lisibles
#Pour faire apparaître les différentes sortes de variables
graph_jacques<-node_status(graph_jacques)
ggplot(data=graph_jacques[[1]],
aes(x=x,
y=y,
xend=xend,
yend=yend,
color=status,
fill=status
))+
geom_dag_edges_link()+
geom_dag_point(size=16,
alpha=0.5)+
geom_dag_label_repel(aes(label=label),
color="black",
size=4,
alpha=0.5,
show.legend = FALSE,
nudge_x = 0.1,
nudge_y=0.1)+
scale_color_viridis(discrete=TRUE,
na.value = "grey85",
option="magma",
begin=0.3,
end=0.7,
labels=c("Intervention",
"Résultat"))+
scale_fill_viridis(discrete=TRUE,
na.value = "grey85",
option="magma",
begin=0.3,
end=0.7,
labels=c("Intervention",
"Résultat"))+
theme_void()+
expand_plot(expand_y = expansion(c(0.2, 0.2)))+
theme(legend.title = element_blank(),
text=element_text(size=12),
strip.text.x = element_text(size=12))## Warning: Using the `size` aesthetic in this geom was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` in the `default_aes` field and elsewhere instead.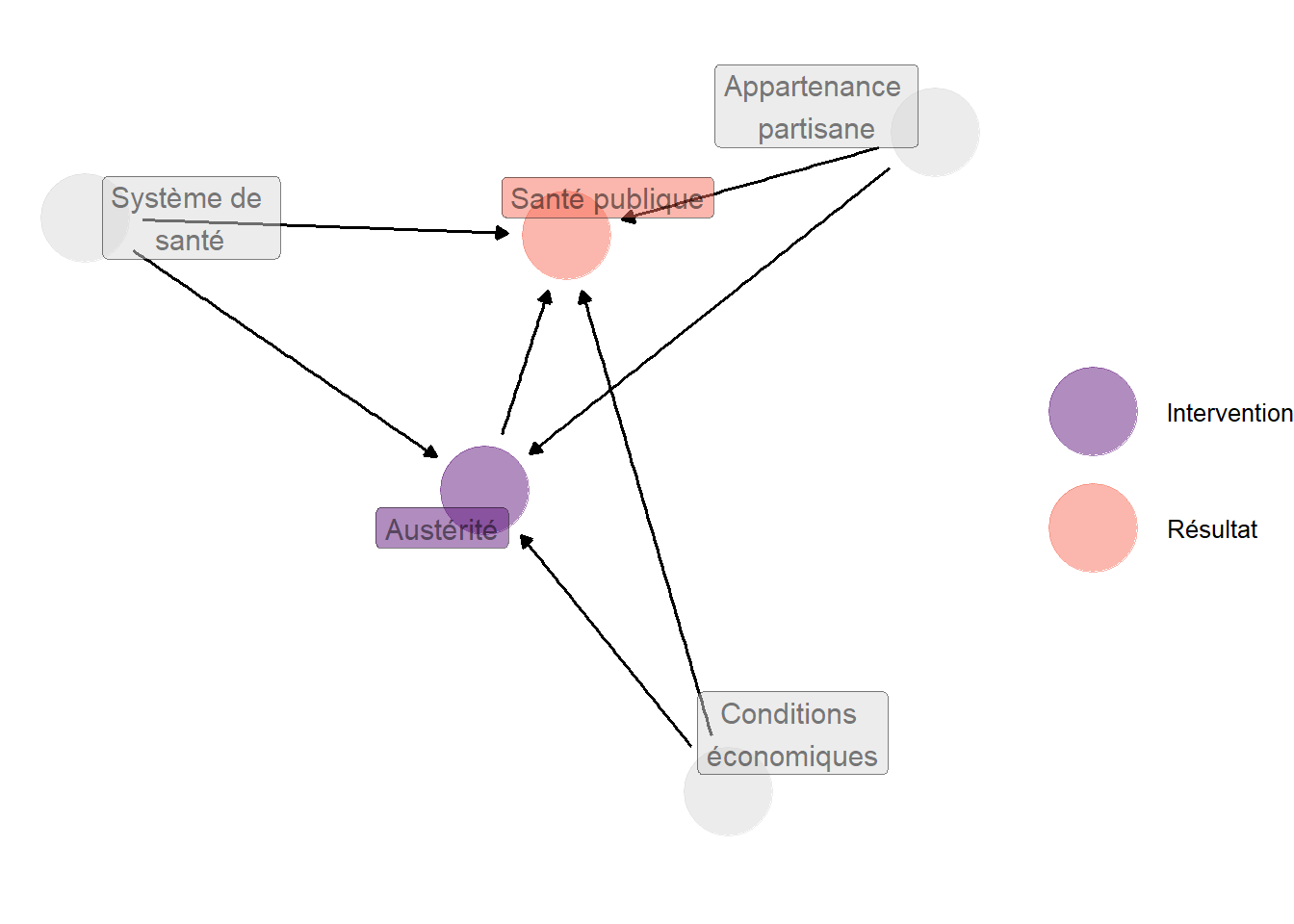
Figure 4.2: Représentation graphique du flot de causalité dans Jacques et Noël (2022). Les différentes variables sont représentées par des nœuds, et les flèches représentent les relations causales qui les relient.
Le cadre proposé par Pearl (2009) pour ces représentations graphiques plutôt intuitives possède trois propriétés qu’il faut énumérer avant de poursuivre plus loin la discussion. En premier lieu, toutes les variables pertinentes pour le problème considéré doivent être représentées, qu’elles soient observables ou non. En d’autres termes, il importe d’être aussi précis que possible dans la description du problème, en faisant apparaître tant l’information dont on dispose que les variables latentes importantes pour la situation empirique que l’on cherche à explorer.
La seule exception concerne les variables latentes qui n’apparaissent comme cause que d’une seule variable observable, qui sont toujours supposées exister. Certains auteurs parlent de magnification lorsque l’on fait ainsi apparaître ces variables latentes. Représenter ces variables alourdit considérablement les représentations graphiques, et ne change en fait rien à l’analyse que l’on mène à partir du graphique. Ainsi, le graphique suivant est équivalent au graphique précédent.
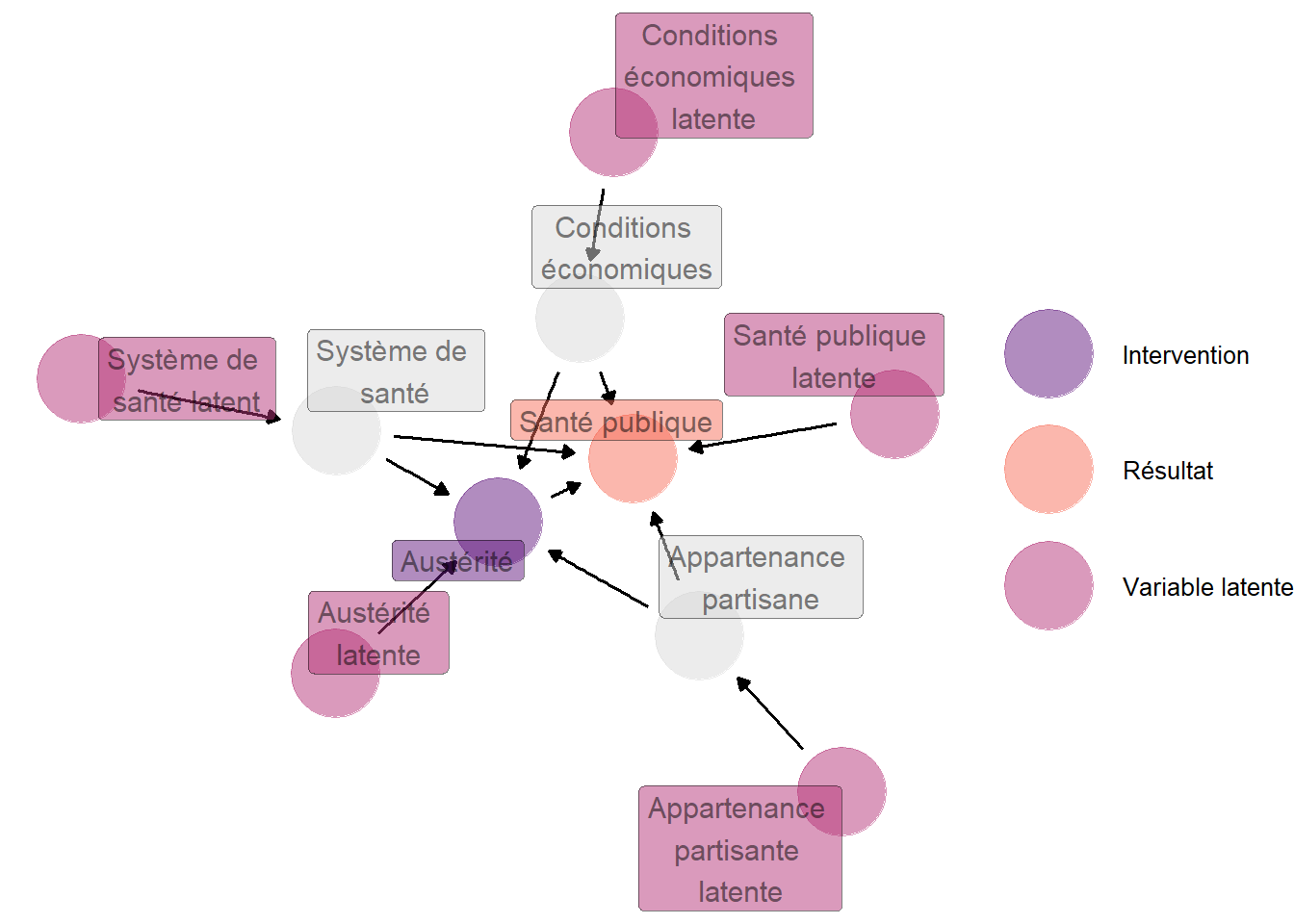
Figure 4.3: Représentation graphique équivalente à celle trouvée dans Jacques et Noël (2022), mais en faisant figurer les variables latentes indépendantes spécifiques à chaque variable observées. Cette représentation graphique ne contient pas d’information supplémentaire par rapport à la précédente mais est relativement plus difficile à lire.
Un deuxième point important est que les relations de causalité entre variables que l’on représente par les flèches sont aussi générales qu’il est possible de l’être. En particulier, lorsque l’on recourt à ces représentations graphiques, on ne fait pas l’hypothèse que que les relations de causalité sont additives et linéaire, ni que les différentes causes ne puissent pas interagir entre elles.
Formellement, lorsque l’on déclare ainsi SantePub~Austerite+AppartParti+SystemeSante+ConditEco, on affirme ainsi qu’il existe :
- une fonction (inconnue) \(f^{SantePub}\) ; et
- une variable latente \(LatSantePub\) indépendante de toutes les autres variables, observées ou latentes ;
telles que : \[SantePub=f^{SantePub}(Austerite, AppartParti, SystemeSante, ConditEco ; LatSantePub)\]
Ainsi, il est par exemple tout à fait possible que lorsque le système de santé admet telle ou telle caractéristiques contrefactuelles, l’austérité en matière de finances publiques n’a pas d’effet sur le niveau et la structure de la dépense de santé publique.
Enfin, le dernier point important est que les techniques fondées sur les représentations graphiques excluent le cas des graphes cycliques, c’est-à-dire des graphes dans lesquels il existe une variable telle qu’en partant de celle-ci et en suivant successivement les flèches, on pourrait revenir à elle. Cela exclut notamment le cas de la simultanéité, c’est-à-dire de la situation que l’on pourrait rencontrer si une variable était cause d’une variable qui cause la première.
Le fragment de code suivant représente deux exemples stylisés de ces graphes cycliques exclus par construction du champ d’investigation.
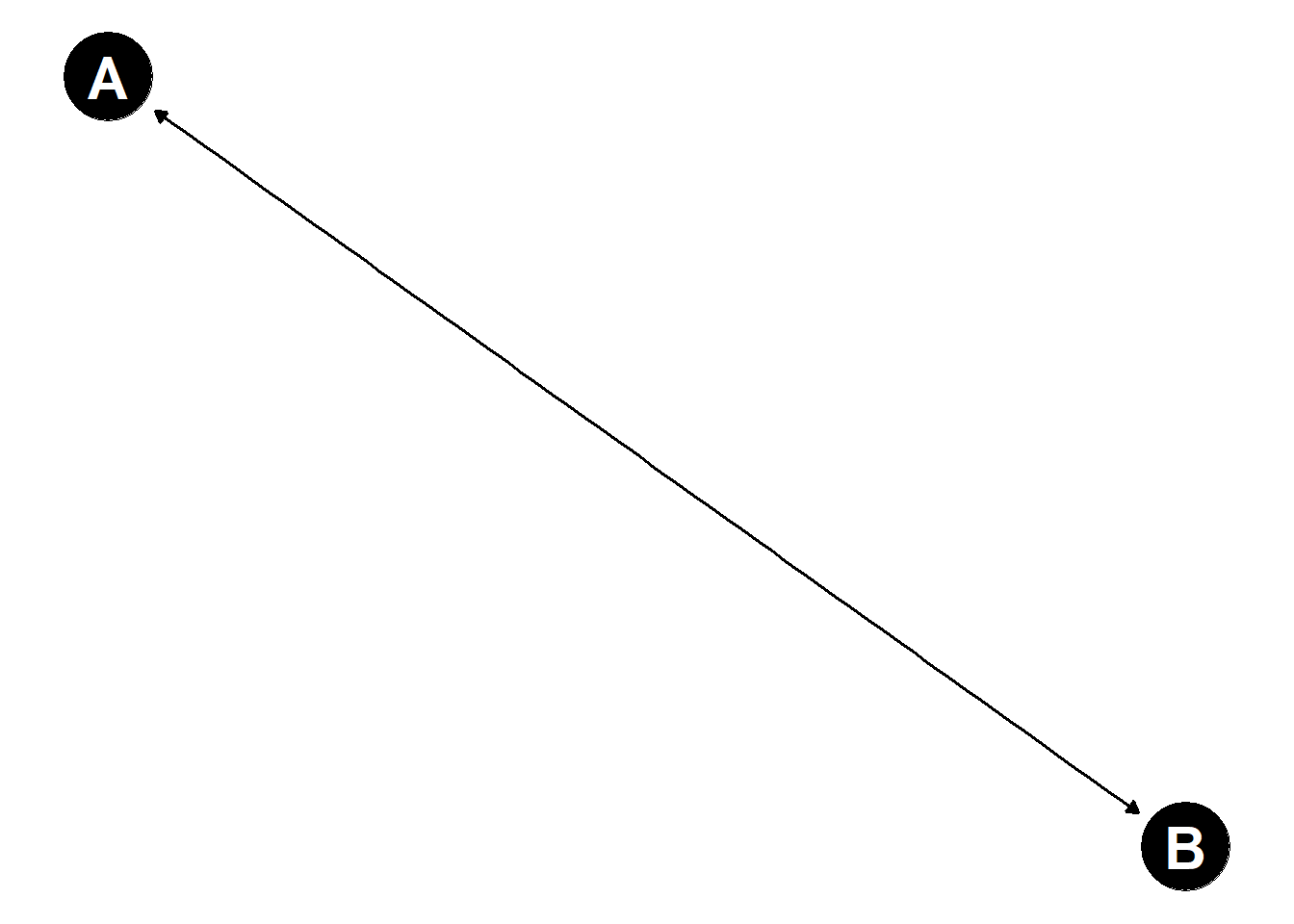
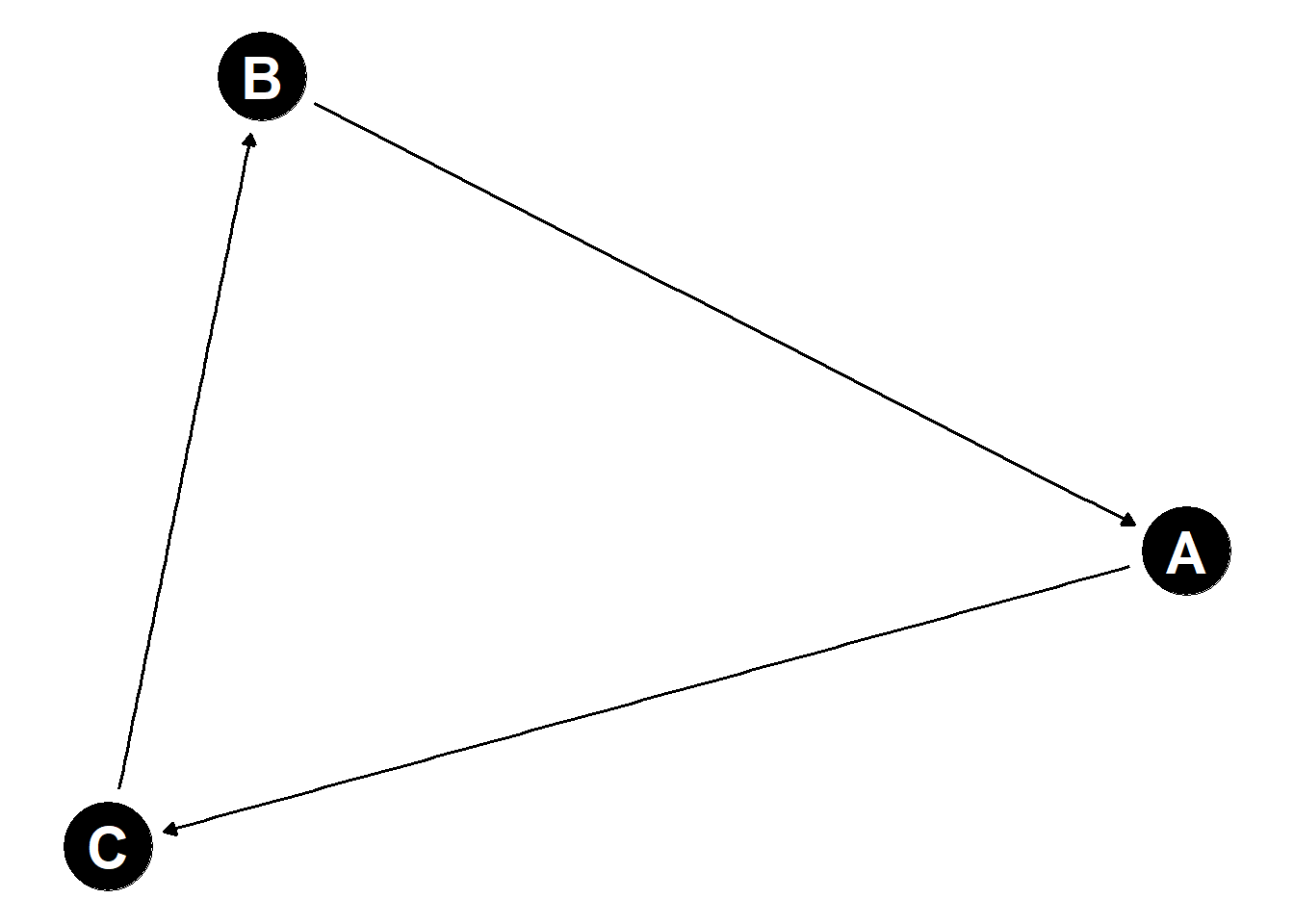
Figure 4.4: Ces graphes sont cycliques : il existe un chemin qui part de A et aboutit à la même variable. En d’autres termes, la variable A est à la fois une cause et une conséquence de B, éventuellement via son effet sur une autre variable.
Définition
Les relations de causalité peuvent être représentées dans des graphes acycliques orientés, c’est-à-dire des graphes où (i) les variables sont représentées par des nœuds ; (ii) le flot de causalité est représenté par des flèches; et (iii) il n’est pas possible en partant d’un nœud et en suivant successivement les flèches qui les lient de revenir au nœud initial.
Il est fréquent d’employer à propos de ces graphes le vocabulaire de la parenté. Ainsi, dans la figure 4.2, on peut dire de la dépense de santé publique qu’elle est une descendante de toutes les autres variables représentées. En d’autres termes, pour toutes les autres variables représentées il est possible en suivant successivement les flèches qui en partent d’aboutir à la variable représentant la dépense de santé publique. Inversement, on dira de ces variables qu’elles comptent parmi les ascendants de la variable de sant publique.
On parle aussi à propos de ces graphes de chemins, qui sont simplement des successions de flèches telles que chaque nouvelle flèche part du nœud où la précédente aboutit. Ces chemins peuvent être orientés, c’est-à-dire qu’ils suivent les flèches successives vont toutes dans le même sens : c’est le cas dans l’exemple considéré du chemin Conditions économiques \(\longrightarrow\) Austérité \(\longrightarrow\) Santé publique. On peut aussi considérer des chemins non-orientés, où les flèches ne se succèdent pas nécessairement dans cet ordre. Ce serait par exemple le cas du chemin Conditions économiques \(\longrightarrow\) Austérité \(\longleftarrow\) Système de santé.
4.3.1.2 Quel est le graphe d’une expérience naturelle ?
En repartant de l’exemple de Jacques et Noël (2022), supposons que le graphe soit considérablement simplifié et ne fasse figurer que deux nœuds correspondant d’une part à l’austérité, et d’autre part à la dépense de santé publique, reliés par une flèche qui part de la première et aboutit à la seconde. La figure 4.5 représente ce graphe hypothétique.
Conformément à ce qui précède, cela implique en premier lieu que l’austérité dépend exclusivement, via une fonction général et inconnue, d’une variable latente aléatoire indépendante de toutes les autres variables du problème. En d’autres termes, la variable aléatoire qui représente l’austérité peut elle-même être considérée comme une variable aléatoire indépendante de toutes les autres variables du problème. En particulier, elle est indépendante de toutes les valeurs potentielles de la dépense de santé publique : on se ramène ainsi à la situation typique d’une expérience aléatoire contrôlée ou d’une expérience naturelle. Par conséquent, on peut traiter la situation hypothètique comme telle : les variations de la dépense publique moyenne avec l’austérité identifient bien les effets causaux moyens de l’austérité sur la dépense de santé publique.
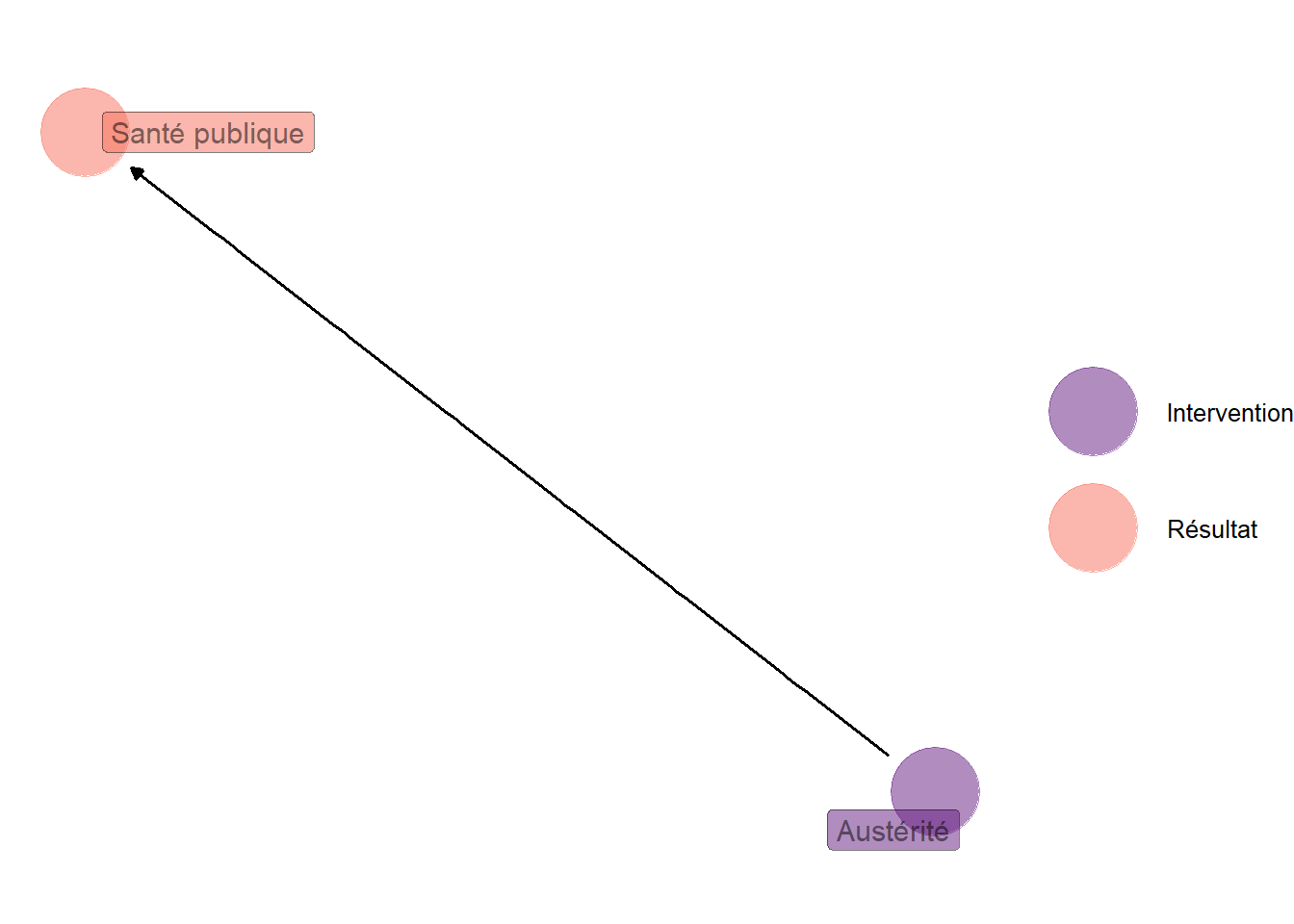
Figure 4.5: Graphe hypothétique simplifié à partir de Jacques et Noël (2022). Il n’y a plus que deux variables liées entre elles par une flèche qui va de l’austérité vers la dépense de santé publique. L’austérité dépend donc exclusivement d’une variable latente inobservée, indépendante de toutes les autres variables : la situation peut être assimilée à une expérience aléatoire contrôlée, ou à une expérience naturelle.
4.3.2 Conditionner sur une variable observable
On peut légèrement complexifier la situation en considérant un graphe légèrement plus riche construit en simplifiant la proposition originale de Jacques et Noël (2022). Cette fois-ci, on fait figurer non seulement l’austérité et la dépense de santé publique, mais encore les conditions économiques. La figure 4.6 représente ce graphe hypothétique.
Dans la situation décrite par ce graphe, il n’est plus possible de raisonner comme si l’on faisait face à une expérience aléatoire contrôlée. En effet, si la dépense de santé publique varie selon que l’austérité se fait plus ou moins prononcée, cela peut certes venir du chemin qui relie l’austérité à la dépense de santé publique, c’est-à-dire de l’effet causal de l’austérité sur la dépense de santé publique, mais cela peut tout aussi bien traduire le fait que tant l’austérité que la dépense de santé publique sont les conséquences d’une même cause, à savoir les conditions économiques. Ainsi, la simple considération des contrastes entre pays exposés à des niveaux différents d’austérité n’informe pas sur l’effet causal de l’austérité sur la dépense de santé publique : il pourrait exister des différences entre pays faisant face à une austérité plus ou moins prononcée même si la flèche qui relie l’austérité à la dépense de santé publique était manquante.
La situation n’est toutefois pas désespérée ! Dans la mesure où les conditions économiques sont observées, on va pouvoir considérer des groupes de pays faisant face à des conditions économiques identiques. Au sein de tels groupes, les conditions économiques ne varient pas, de sorte que si ces pays font face à des niveaux d’austérité plus ou moins prononcés, c’est seulement parce que leur niveau d’austérité latente diffère. Comme celle-ci est indépendante de toutes les autres variables considérées dans le problème, on se ramène ainsi à une situation assimilable à celle d’une expérience aléatoire contrôlée ou d’une expérience naturelle. En définitive, comme cette assimilation est valable à l’intérieur de strates définies par les conditions économiques, on identifie la situation empirique à celle de l’expérience aléatoire stratifiée, et les conditions d’identification des effets causaux moyens sont les mêmes.
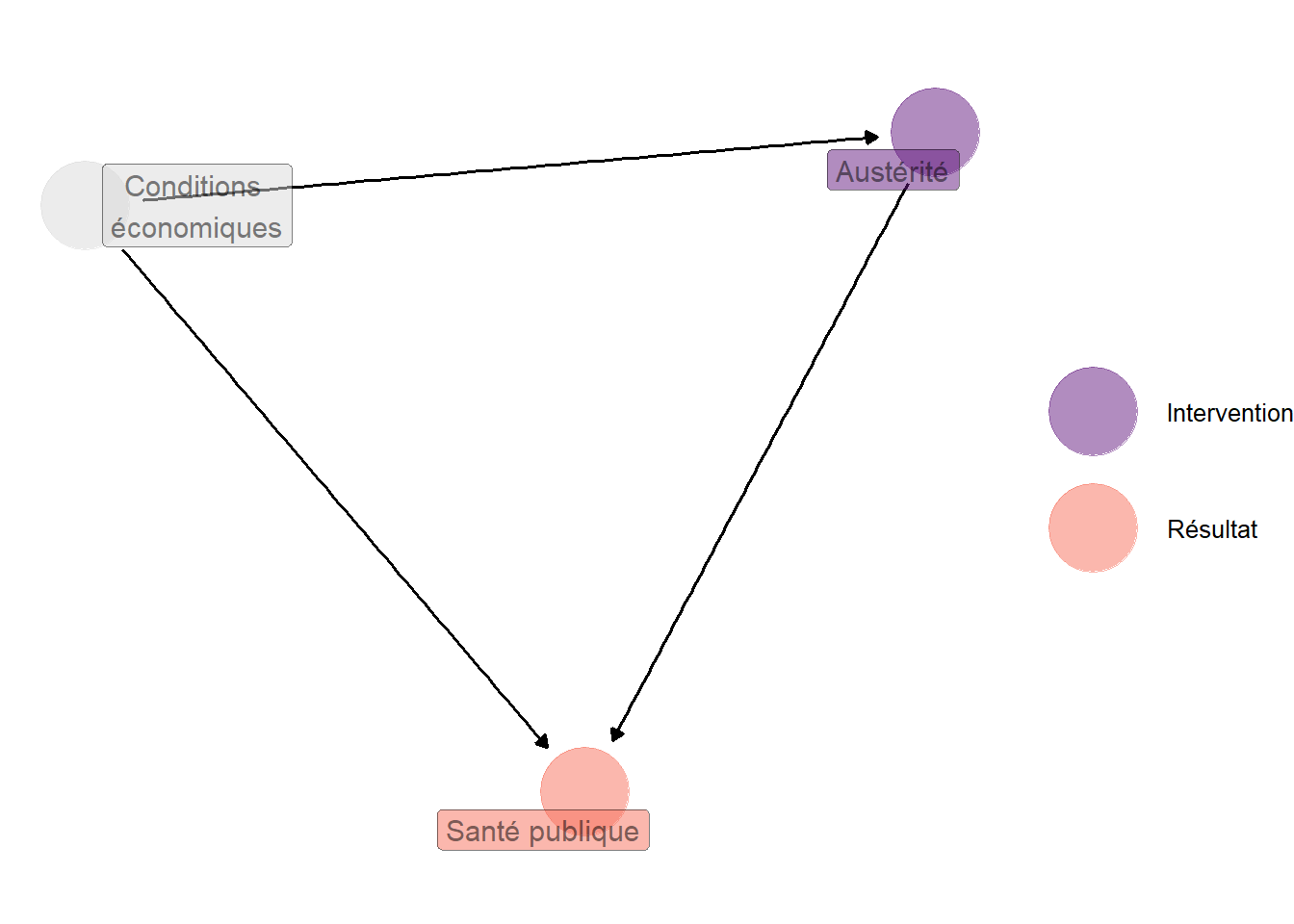
Figure 4.6: Graphe hypothétique simplifié à partir de Jacques et Noël (2022). Dans ce cas, les variations de la dépense moyenne de santé publique avec le niveau d’austérité n’informent plus sur les effets causaux moyens de l’austérité sur la dépense de santé publique. En effet, si la dépense de santé publique varie quand l’austérité se fait plus ou moins forte, c’est peut-être que l’austérité a un effet causal non-nul sur la dépense de santé publique, mais cela peut tout aussi bien refléter que tant l’austérité que la dépense de santé publique sont des conséquences d’une cause commune : les conditions économiques.
Dans cet exemple hypothétique, on parvient donc à identifier les effets causaux moyens de l’austérité dés lors que l’on se place dans des strates de pays dans lesquels les conditions économiques sont les mêmes. On dit souvent que l’on conditionne sur les conditions économiques, ce qui signifie simplement qu’au lieu de considérer l’espérance conditionnelle \(\mathbb{E}[S \mid A]\), où \(S\) serait la dépense de santé publique et \(A\) la variable représentant l’austérité, on considère plutôt l’espérance conditionnelle \(\mathbb{E}[S \mid A, \, C]\) où \(C\) correspond aux conditions économiques. En d’autres termes, on fait la comparaison de pays connaissant des conditions économiques semblables, mais des niveaux d’austérité différents.
Dans le langage développé par Pearl (2009), on dit dans la situation étudiée que conditionner sur les conditions économiques permet de bloquer la porte de sortie (backdoor en anglais), c’est-à-dire le chemin non-orienté qui lie austérité et dépense de santé publique et dont une des extrémités est une flèche qui débouche sur la variable représentant l’austérité. Pour le dire autrement, cela signifie qu’en se plaçant dans des groupes de pays dans lesquels les conditions économiques sont les mêmes, on parvient à neutraliser la corrélation entre austérité et dépense de santé publique qui naît du chemin Austérité \(\longleftarrow\) Conditions économiques \(\longrightarrow\) Santé publique.
4.3.3 Y a-t-il de mauvaises variables de conditionnement ?
La discussion qui précède implique-t-elle qu’il soit bon de conditionner par n’importe quelle variable qui se trouverait dans une porte de sortie, c’est-à-dire dans un chemin non-orienté qui relie intervention et résultat, et dont une des extrémités est une flèche qui pointe vers l’intervention ? La réponse à cette question est négative, et ce pour au moins deux raisons.
4.3.3.1 Chaînes de médiation
La première raison pour cela est que pour un nœud, appartenir à une porte de sortie n’exclut pas d’appartenir à un autre chemin qui lie intervention et résultat. En particulier, cela n’exclut absolument pas d’appartenir à une chaîne de médiation c’est-à-dire à un chemin orienté qui part de l’intervention et aboutit au résultat. Un exemple d’une telle situation serait celle où l’on s’intéresse aux effets de l’éducation sur le salaire perçu sur le marché du travail, et où l’on considérerait que le graphe très simple 4.7 est une représentation raisonnable de la réalité.
Ici, le salaire dépend directement de la formation reçue d’une part, et de la profession exercée d’autre part. Le problème que l’on rencontre est qu’il y a bien une porte de sortie : la formation reçue n’est pas attribuée au hasard et indépendamment de toutes les autres grandeurs du problème, mais dépend en fait de l’origine familiale, qui joue également sur la profession exercée. Ainsi, salaire et éducation sont non seulement liés par le chemin direct Formation initiale \(\longrightarrow\) Salaire, mais aussi par la porte de sortie Formation initiale \(\longleftarrow\) Origines sociales \(\longrightarrow\) Profession exercée \(\longrightarrow\) Salaire, et enfin par le chemin Formation initiale \(\longrightarrow\) Profession exercée \(\longrightarrow\) Salaire.
Est-il raisonnable de prétendre identifier les effets de la formation initiale sur le salaire en conditionnant sur la profession exercée, c’est-à-dire, par exemple, en ne comparant entre eux que des salariés occupant un poste de cadre ? Dans le cas présent, cela n’est pas souhaitable dans la mesure précisément où un des canaux importants par lequel l’éducation a un effet en général positif sur le salaire, c’est en permettant l’accès à des postes dont le statut est plus élevé. Ainsi, si on ne compare entre eux que des cadres ayant des niveaux d’éducation différents, on risque vraisemblablement de sous-estimer l’effet moyen de l’éducation sur le salaire.
À retenir
Il est essentiel dans le choix de l’ensemble des variables de conditionnement de s’abstenir de retenir des variables qui appartiennent à une chaîne de médiation qui part de l’intervention et aboutit au résultat (Intervention \(\longrightarrow\) … \(\longrightarrow\) Résultat), ou même par n’importe quelle variable qui est une descendante d’une des variables appartenant à une chaîne de médiation.
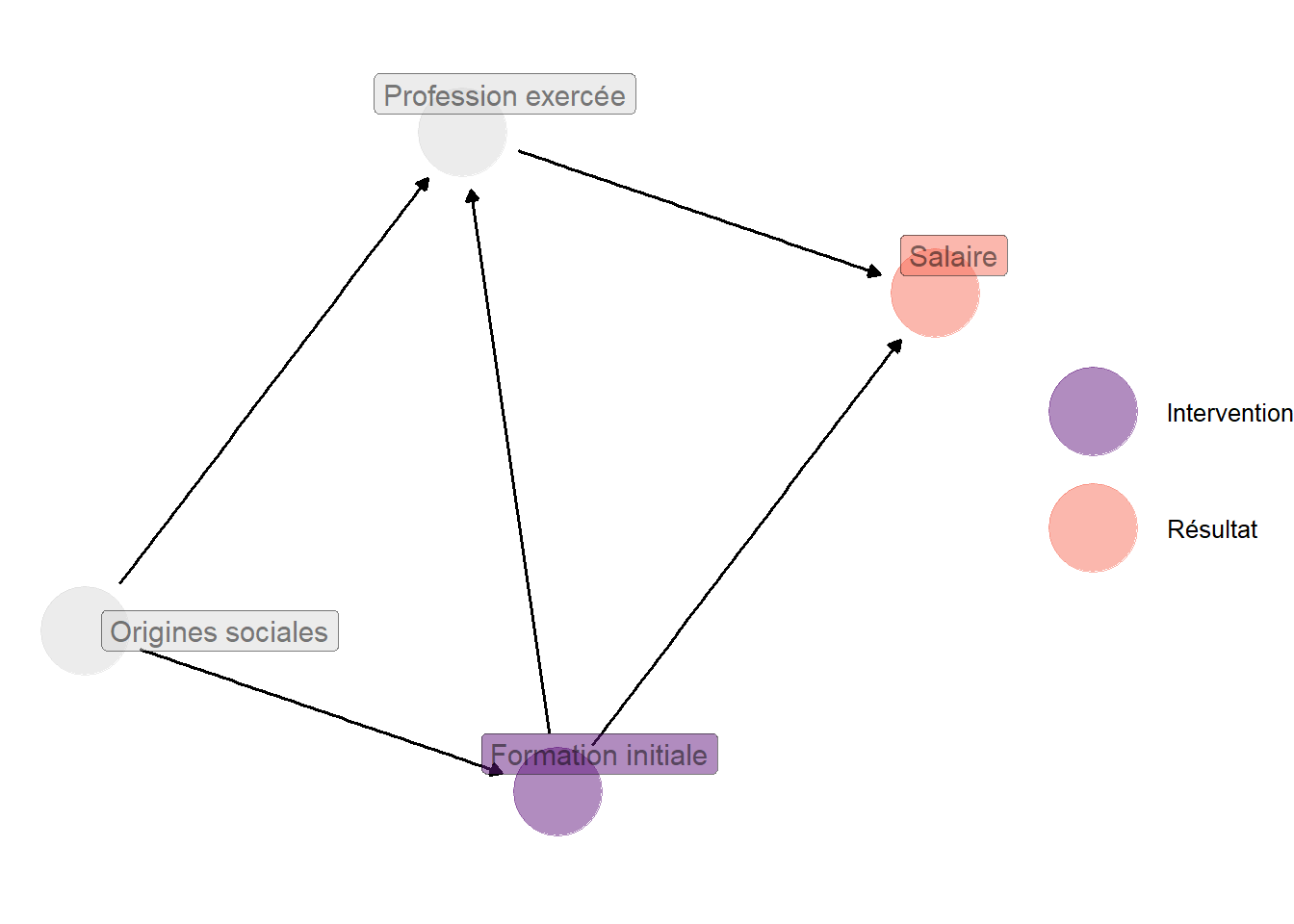
Figure 4.7: Graphe hypothétique d’une étude des effets de la formation initiale sur le salaire. La profession exercée se trouve à la fois sur la porte de sortie Formation initiale \(\longleftarrow\) Origines sociales \(\longrightarrow\) Profession exercée \(\longrightarrow\) Salaire, et sur la chaîne de médiation Formation initiale \(\longrightarrow\) Profession exercée \(\longrightarrow\) Salaire.
4.3.3.2 Notion de biais de collision
Le cas de la chaîne de médiation est celui dans lequel, en conditionnant par une variable intermédiaire, on va en quelque sorte couper une partie de l’effet de l’intervention. Un autre danger dans le choix des variables de conditionnement est celui où, en restreignant les groupes au sein desquels on fait les comparaisons, on fait apparaître une corrélation qui ne reflète pas d’effet causal, et est nulle lorsque l’on considère la population tout entière.
Pour s’en rendre compte, on peut considérer la situation étudiée par Knox, Lowe et Mummolo (2020) dans un article consacré aux éventuels biais racistes des policiers étatsuniens dans l’usage de la force. Schématiquement, la question est de savoir si, lors d’une rencontre entre un civil d’une part, et un ou des policiers d’autre part, l’appartenance du civil à une minorité a un effet causal sur l’usage de la force. Cet usage de la force dépend potentiellement de cette appartenance minoritaire du civil d’une part, mais également du caractère plus ou moins suspect de son activité – selon le ou les policiers – que l’on peut, au moins au premier abord, supposé ne pas dépendre de ce statut minoritaire. Ce caractère plus ou moins suspect demeure cela étant inobservable du point de vue qui est le nôtre, et doit donc être traité comme une variable latente. Le premier panneau de la figure 4.8 représente le graphe correspondant à cette investigation.
Si la situation étudiée était bien celle-ci, alors comparer Blancs et Noirs du point de vue de l’usage de la force par les forces de l’ordre permettrait bien d’identifier les biais racistes éventuels de la police, représentés par la flèche Minorité \(\longrightarrow\) Usage de la force. Mais Knox, Lowe et Mummolo (2020) argumentent que ce graphe est en réalité une description incomplète de la situation étudiée. En effet, les données disponibles ne portent en réalité par sur toutes les interactions entre civils et policiers, mais seulement sur un sous-ensemble d’interactions enregistrées, pour lesquelles le ou les civils font l’objet d’un contrôle par les forces de l’ordre. Le graphe complet doit donc faire figurer non seulement l’usage de la force, mais également le contrôle et l’enregistrement de l’interaction, ce qui demande de faire apparaître un nouveau nœud dans le graphe. Ici encore, il semble vraisemblable de faire dépendre cette décision de contrôle du statut minoritaire des civils d’une part, et du caractère suspect de leur activité d’autre part. Le second panneau de la figure 4.8 représente le graphe correspondant.
Schématiquement, parce que l’on conditionne sur le fait d’avoir eu un contrôle, ce qui résulte déjà en partie de biais racistes potentiels, les interactions enregistrées contiennent donc (i) des interactions de policiers avec des civils Noirs dont l’activité n’est pas particulièrement suspecte (ii) des interactions de policiers avec des civils Noirs dont l’activité est suspecte et (iii) des interactions de policiers avec des civils Blancs dont l’activité est suspecte. De la sorte, si le caractère suspect de l’activité rend plus probable l’usage de la force, alors la comparaison entre interactions avec des civils Blancs et interactions avec des civils Noirs dans ces données va grandement sous-estimer l’usage de la force envers les civils Noirs comparables aux civils Blancs. C’est à cela que Knox, Lowe et Mummolo (2020) attribuent le fait que la majorité des travaux antérieurs aux leurs sur la question ne détectent pas de biais racistes dans l’usage de la force par les policiers étatsuniens.
À retenir
Lorsque deux nœuds sont liées via un troisième par une fourchette inversée de la forme \(A \longrightarrow X \longleftarrow B\), conditionner sur la variable \(X\) fait apparaître une corrélation entre \(A\) et \(B\) qui n’est pas informative quant à l’effet causal de \(A\) sur \(B\), ni quant à l’effet causal de \(B\) sur \(A\). Dans le choix des variables de conditionnement, si une porte de sortie présente une telle fourchette inversée, alors cette porte de sortie est déjà bloquée et il faut s’abstenir de conditionner par une des variables qu’elle contient. Enfreindre cette règle génère un biais de collision.
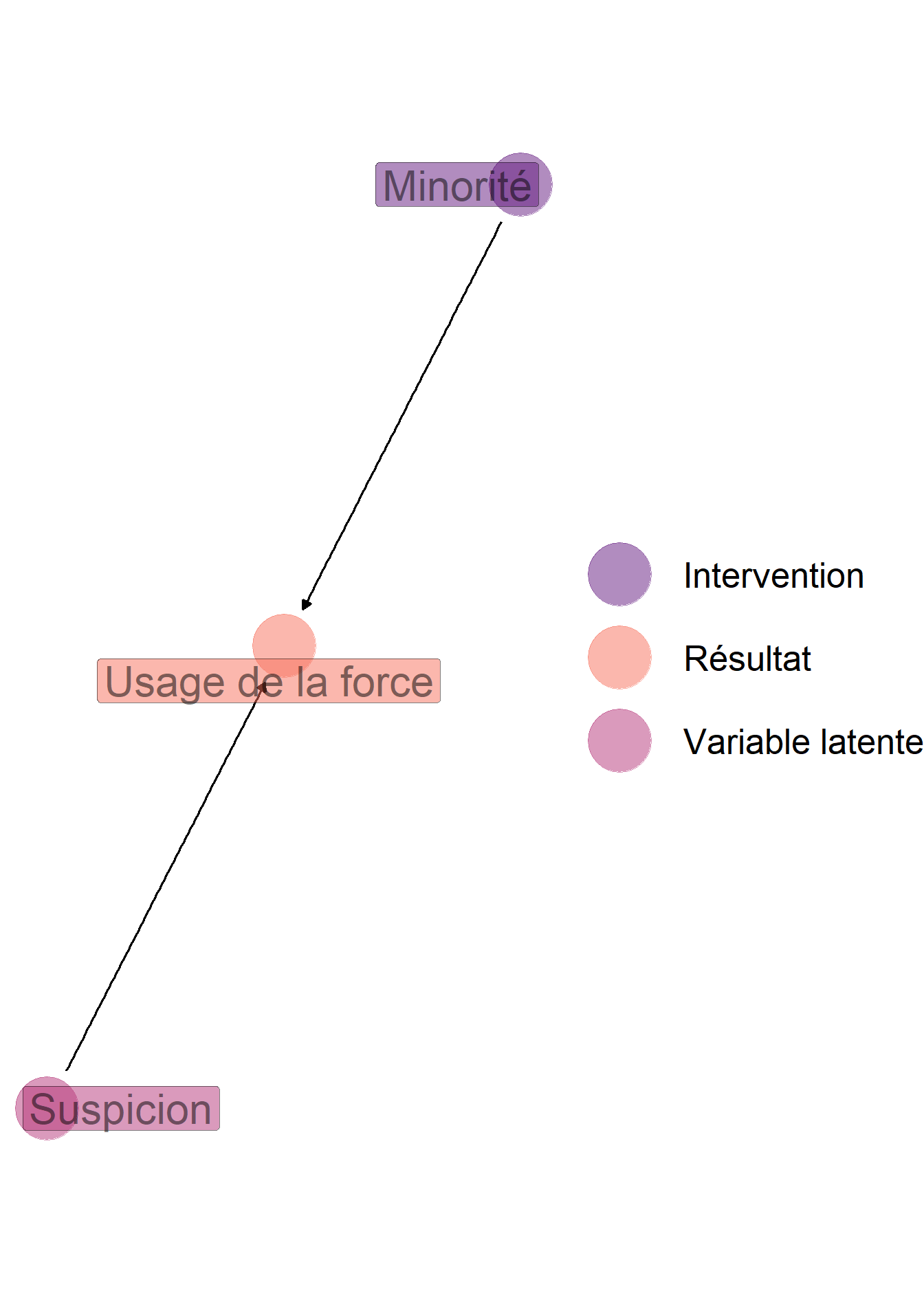

Figure 4.8: Représentations graphiques adaptées de Knox, Lowe et Mummolo (2020) sur l’étude des biais racistes éventuels de la police étatsunienne. Dans la situation décrite à gauche, la simple comparaison de l’usage de la force lors des interactions avec des Blancs et des Noirs renseigne sur ces éventuels biais. Dans le second cas, lorsque l’on se restreint aux interactions qui ont fait l’objet d’un enregistrement dans les données utilisées pour faire cette comparaison, et donc lorsque l’on conditionne sur le fait qu’un contrôle a eu lieu, on fait apparaître une corrélation entre le statut minoritaire et le caractère suspect de l’activité, de sorte que la comparaison entre Blancs et Noirs sous-estime largement l’usage de la force vis-à-vis des Noirs lors d’interactions comparables.
4.3.4 Stratégie backdoor
Les exemples précédents permettent de montrer que :
- conditionner sur une ou plusieurs variables observables permet parfois d’identifier des effets causaux moyens ;
- conditionner sur certaines variables observables peut au contraire empêcher cette identification, en particulier si :
- ces variables sont des médiateurs de l’effet de l’intervention sur la dimension d’intérêt, ou ;
- conditionner sur ces variables crée une corrélation entre des variables non-apparentées, parce que l’on fait apparaître ainsi un biais de collision.
Tous ces éléments peuvent se combiner en un jeu de règles qui régissent ce que Pearl (2009) appelle stratégie backdoor, à savoir la stratégie qui consiste à choisir à partir d’une représentation graphique du problème un ensemble de variables de conditionnement. En d’autres termes, cette stratégie consiste simplement à utiliser les graphes pour déterminer au sein de quels groupes, s’ils existent, il est possible de comparer des individus selon qu’ils aient fait ou non l’objet de l’intervention pour en déduire les effets causaux moyens de celle-ci.
À retenir
Il est parfois possible d’identifier les effets causaux moyens en invoquant l’hypothèse d’indépendance conditionnelle, c’est-à-dire en faisant l’hypothèse qu’à l’intérieur de certains groupes, l’intervention est le résultat d’une expérience aléatoire contrôlée, ou d’une expérience naturelle. Pour ce faire, ces groupes doivent être définis en fixant la valeur de certaines variables observables bien choisies. Un tel ensemble (éventuellement vide) de variables doit à la fois (i) bloquer toutes les portes de sortie qui débouchent sur l’intervention et (ii) ne bloquer aucune des chaînes de médiation qui vont de l’intervention au résultat étudié.
Une porte de sortie débouchant sur l’intervention est bloquée si :
- elle contient une flèche qui aboutit à une des variables sur laquelle on conditionne \(A \longrightarrow X\) ;
- elle contient deux flèches qui partent d’une variable sur laquelle on conditionne \(A \longleftarrow X \longrightarrow B\) ;
- elle contient une fourchette inversée \(A \longrightarrow Z \longleftarrow B\) telle que ni \(Z\) ni aucun de ses descendants n’appartienne à l’ensemble des variables sur lesquelles on conditionne.
Avec cette stratégie en tête, on peut revenir à l’exemple initial de Jacques et Noël (2022) et considérer de nouveau la représentation graphique que l’on en a tirée. Ici, on a trois portes de sortie qui débouchent sur la variable désignant le niveau d’austérité. Pour chacune de ces portes de sortie, on dispose d’une variable observable de laquelle partent deux flèches : on peut donc mettre en place une stratégie backdoor. En définitive, ce graphe justifie de conditionner sur ces trois variables, c’est-à-dire de comparer des pays connaissant les mêmes conditions économiques, dont le gouvernement a la même appartenance partisane, et dont le système de santé fonctionne de la même façon, mais dont les niveaux d’austérité sont différents pour connaître les effets de celui-ci sur la dépense de santé publique.
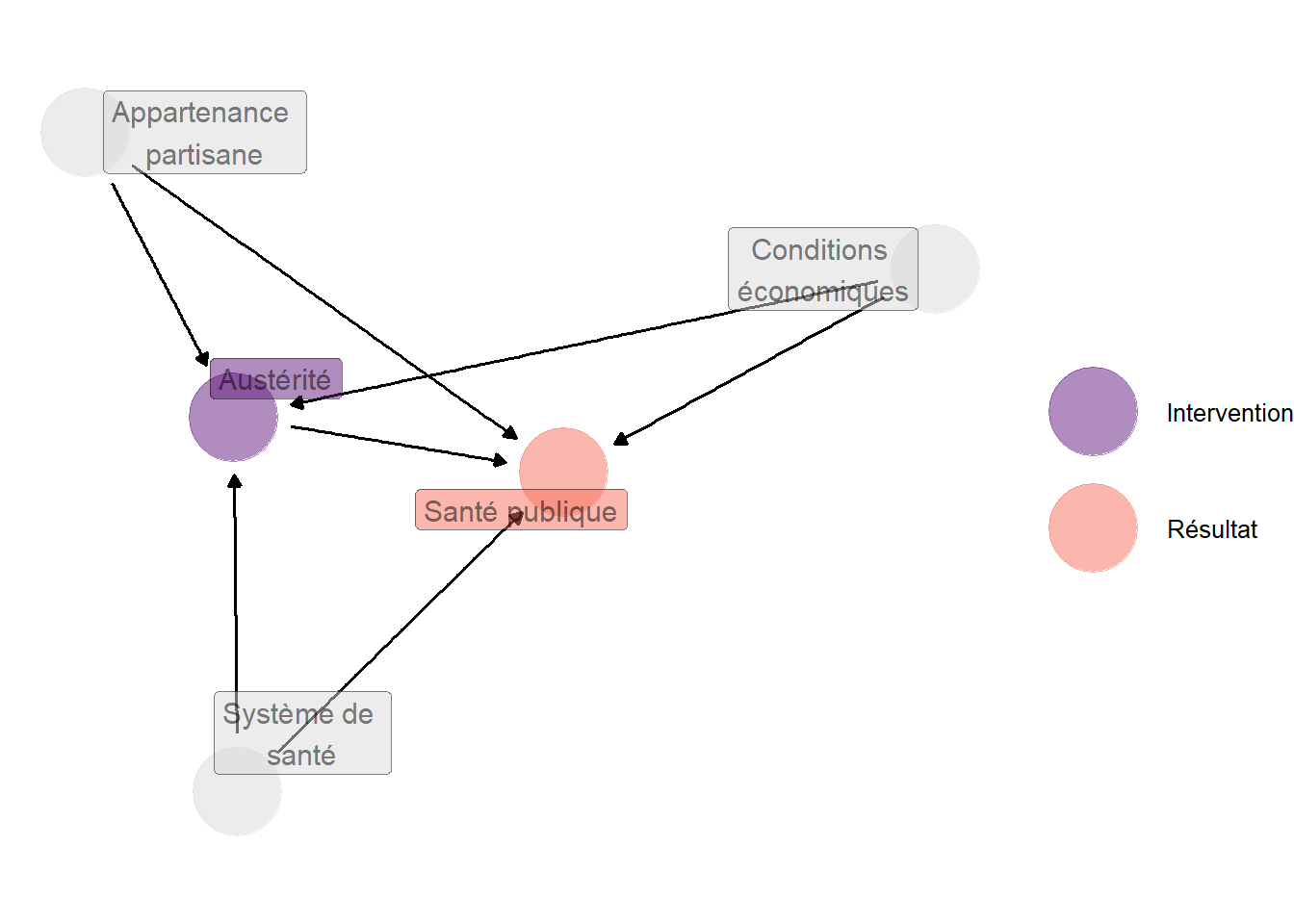
Figure 4.9: Représentation graphique du flot de causalité dans Jacques et Noël (2022). Il y a trois portes de sortie, que l’on peut bloquer en conditionnant sur les conditions économiques, l’appartenance partisane du gouvernement et le système de santé public. En d’autres termes, comparer des pays connaissant des conditions économiques similaires, dont le gouvernement a la même appartenance partisane et le système de santé fonctionne de la même façon, mais qui connaissent des niveaux d’austérité différents permet d’identifier les effets de celle-ci sur le niveau et la structure de la dépense de santé publique.
Plusieurs éléments importants doivent être notés au sujet de ce qui précède :
- il peut exister plusieurs solutions différentes au problème, c’est-à-dire plusieurs choix d’ensemble de variables sur lesquelles il est possible de conditionner pour identifier des effets causaux ;
- une de ces solutions peut-être l’ensemble vide, auquel cas la comparaison des individus selon les valeurs prises par la variable représentant l’intervention suffit à en identifier les effets causaux moyens ;
- l’ensemble des solutions peut également être vide, ce qui signifie qu’il n’existe pas de solution au problème (ce qui ne signifie pas la même chose que la proposition précédente).
En d’autres termes, le choix de l’ensemble des variables sur lesquelles il faut conditionner n’est pas toujours univoque, il est parfois tout à fait justifier de ne pas conditionner, et enfin le conditionnement même bien choisi ne permet pas toujours d’identifier des effets causaux moyens.
4.3.5 Quel usage des approches graphiques ?
Les résultats précédents fournissent des conditions auxquelles on peut espérer trouver un ensemble de variables de conditionnement, c’est-à-dire un défintion des groupes au sein desquelles la comparaison selon les différentes valeurs de la variable d’intervention est informative sur les effets causaux moyens de cette intervention. Cela étant, utiliser ces conditions pour déterminer un ensemble satisfaisant dans des cas non-triviaux n’est pas aisé.
Un des avantages de la représentation sous forme de graphe est qu’il est possible de recourir à des approches algorithmiques assez efficace pour ce faire. En plus de la facilité avec laquelle il permet de générer des figures pour ces représentations graphiques, c’est là un des intérêts du packages ggdag.
Le fragment de code suivant reprend l’exemple de Jacques et Noël (2022) en montrant une façon d’utiliser les fonctions de ce package pour déterminer un ensemble de conditionnement. En utilisant la fonction dag_paths, il est dans un premier temps possible de récupérer les portes de sortie qui débouchent sur la variable représentant le niveau d’austérité. La fonction dag_adjustment_sets permet de calculer à partir du graphe les ensembles de variables de conditionnement possibles.
library(ggdag)
library(ggplot2)
library(viridis)
library(data.table)
graph_jacques<-dagify(SantePub~Austerite+AppartParti+SystemeSante+ConditEco,
#Pour chaque nœuds auquel aboutit au moins une flèche,
# on recense d'où partent toutes ces flèches
Austerite~AppartParti+SystemeSante+ConditEco,
exposure = "Austerite",
#La variable qui correspond à l'intervention dont on
# souhaite étudier les effets
outcome = "SantePub",
#La variable qui correspond aux conséquences que l'on
# voudrait pouvoir mesurer
labels = c("SantePub"="Santé publique",
"Austerite"="Austérité",
"AppartParti"="Appartenance \npartisane",
"SystemeSante"="Système de \nsanté",
"ConditEco"="Conditions \néconomiques"))
#La fonction dag_paths permet de récupérer tous les chemins (non-orientés) qui
# relient l'intervention à la variable de résultat
chemins<-data.table(dag_paths(graph_jacques)[[1]])
#Parmi ces chemins, on ne veut garder que ceux qui ouvrent une porte de sortie,
# c'est-à-dire qui ont une flèche qui débouche sur l'intervention
#On récupère d'abord le statut de toutes les variables
statut<-data.table(node_status(graph_jacques)[[1]])
#On récupère seulement les chemins qui ouvrent une porte de sortie sur
# l'intervention, c'està-dire ici l'austérité
depart_backdoor<-chemins[
path=="open path"
#chemin ouvert entre intervention et résultat
& to %in% statut[status=="exposure"]$name
#une flèche débouche sur l'intervention
]
#On récupère enfin les portes de sortie en entier, c'est-à-dire des chemins
# constitués de flèches dont la première aboutit à la variable d'intervention
# et les autres se suivent (sans orientation) jusqu'à la variable de résultat
backdoor<-chemins[
set %in% depart_backdoor$set
#On garde les porte de sortie qu'on a repérées
& path=="open path"
#On garde seulement les chemins qui vont de l'intervention au résultat
& !is.na(to)
& !(name %in% statut[status=="exposure"]$name
& to %in% statut[status=="outcome"]$name),
#seules les flèches qui débouchent quelque part nous intéressent
c("set",
"name",
"to")]
backdoor## set name to
## 1: 2 AppartParti Austerite
## 2: 2 AppartParti SantePub
## 3: 3 ConditEco Austerite
## 4: 3 ConditEco SantePub
## 5: 4 SystemeSante Austerite
## 6: 4 SystemeSante SantePub#On récupère un ensemble de variables de conditionnement
conditionner<-data.table(dag_adjustment_sets(graph_jacques)[[1]])
levels(factor(conditionner$set))## [1] "{AppartParti, ConditEco, SystemeSante}"La fonction dag_adjustment_sets est bien capable de repérer les situations dans lesquelles plusieurs ensembles de conditionnement, et de les proposer à l’utilisatrice ou l’utilisateur. Pour ce faire, on peut considérer le petit exemple suivant, inspiré de Jacques et Noël (2022). Dans leur article, les auteurs argumentent que l’effet du type de système de santé sur le niveau et la structure de la dépense de santé publique tient à la fois aux difficultés de financement inhérentes à chaque type de système, et aux possibilités de coordination entre acteurs de santé qu’il laisse. On pourrait donc complexifier le graphe en faisant apparaître ces deux nouveaux nœuds, qui doivent être des enfants du nœud correspondant au type de système de santé, et apparaître comme causes directes de la variable représentant la dépense de santé publique.
Dans ce cas, on a deux portes de sorties distinctes : Austérité \(\longleftarrow\) Système de santé \(\longrightarrow\) Financement du système de santé \(\longrightarrow\) Dépense de santé publique d’une part, et Austérité \(\longleftarrow\) Système de santé \(\longrightarrow\) Coordination des acteurs de santé \(\longrightarrow\) Dépense de santé publique d’autre part. La première est bloquée si l’on conditionne sur le type de système de santé, ou bien sur le financement du système de santé (ou les deux). La seconde est bloquée si l’on conditionne sur le type de système de santé, ou bien sur la coordination entre acteurs de santé (ou les deux).
Ainsi, conditionner sur le type de système de santé suffit à bloquer les deux portes de sortie ; en revanche, si l’on s’abstient de conditionner sur celu-ci, il est nécessaire de conditionner sur les deux autres variables par lesquelles transite l’effet du type de système de santé sur la dépense de santé publique.
La fonction dag_adjustment_sets ne renvoie pas tous les ensembles de variables de conditionnement possibles, mais les ensembles minimaux, c’est-à-dire un ensemble d’ensembles de variables de conditionnement tels qu’aucun ne soit inclus dans l’autre. Par exemple, dans le cas présent, {Système de santé} et {Système de santé, Financement du système de santé} sont deux ensembles possibles, mais le premier est inclus dans le second. La fonction ne renvoie donc que le second.
library(ggdag)
library(data.table)
graph_jacques_multiple<-
dagify(SantePub~Austerite+DiffFinanceSysSan+CoordActSante,
#Pour chaque nœuds auquel aboutit au moins une flèche,
# on recense d'où partent toutes ces flèches
Austerite~SystemeSante,
DiffFinanceSysSan~SystemeSante,
CoordActSante~SystemeSante,
exposure = "Austerite",
#La variable qui correspond à l'intervention dont on
# souhaite étudier les effets
outcome = "SantePub",
#La variable qui correspond aux conséquences que l'on
# voudrait pouvoir mesurer
labels = c("SantePub"="Santé publique",
"Austerite"="Austérité",
"AppartParti"="Appartenance \npartisane",
"SystemeSante"="Système de \nsanté",
"DiffFinanceSysSan"="Financement du \nsystème de \nsanté",
"CoordActSante"="Coordination des \nacteurs de santé",
"ConditEco"="Conditions \néconomiques"))
#On récupère un ensemble de variables de conditionnement
conditionner<-data.table(dag_adjustment_sets(graph_jacques_multiple)[[1]])
levels(factor(conditionner$set))## [1] "{CoordActSante, DiffFinanceSysSan}" "{SystemeSante}"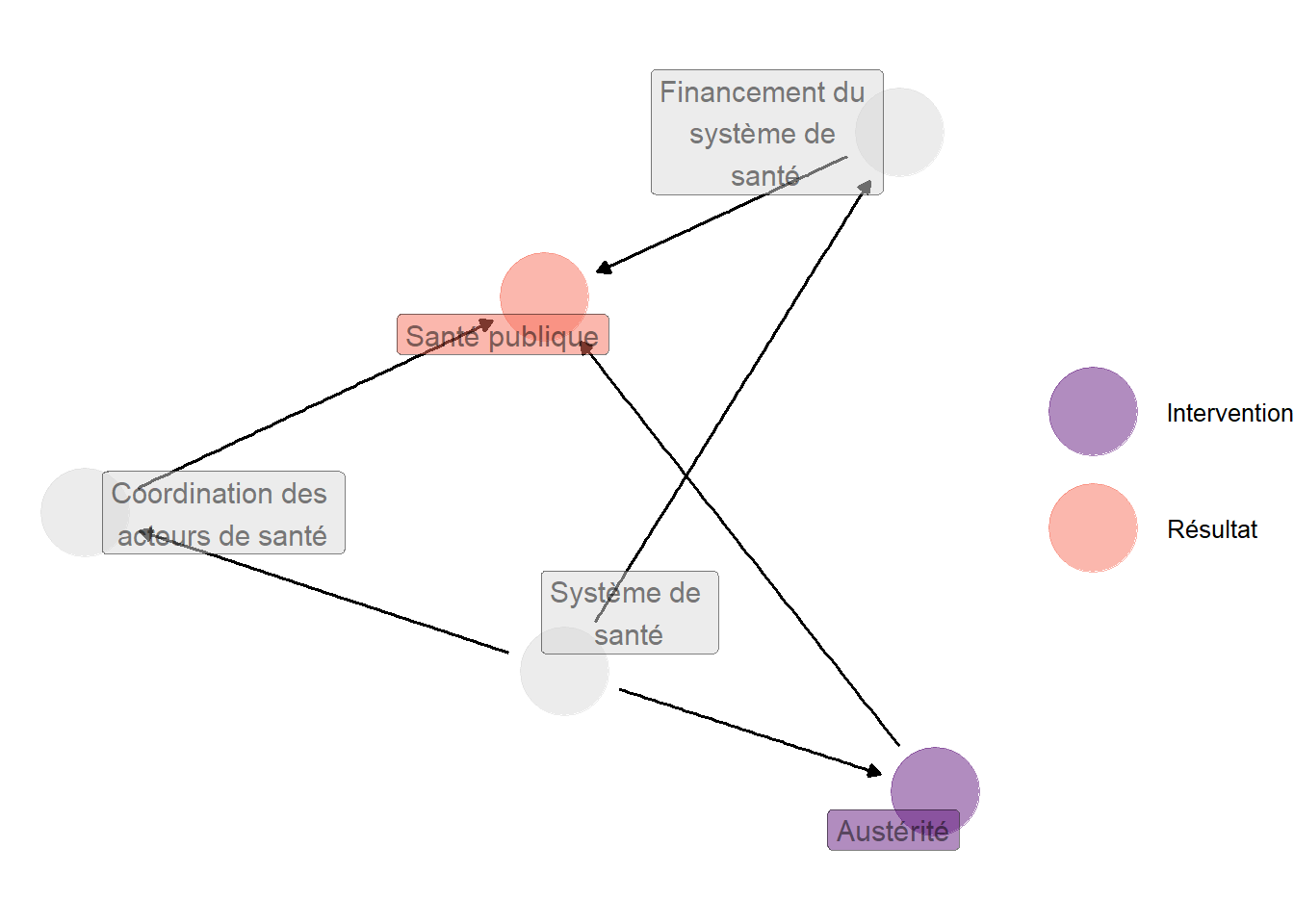
Figure 4.10: Représentation graphique inspirée de Jacques et Noël (2022). Le type de système de santé influe sur le niveau et la structure de la dépense de santé publique à travers les difficultés de financement inhérentes à chaque type de système de santé, et d’autre part à travers les possibilités de coordination qu’il laisse aux acteurs de santé. Dans ce cas, il est possible de bloquer la porte de sortie ou bien en conditionnant sur le type de système de santé, ou bien en conditionnant à la fois sur des variables représentant les difficultés de financement et les possibilités de coordination disponibles pour les acteurs de santé.
La fonction est également capable de repérer les cas où il n’est pas nécessaire de conditionner sur quelque variable que ce soit pour identifier les effets causaux moyens de l’intervention. Ainsi, si l’on reprend le graphe inspiré de Knox, Lowe et Mummolo (2020), la fonction avertit bien que le conditionnement n’est pas nécessaire.
library(ggdag)
dag_race_force_simple<-dagify(force ~ race + suspicion,
exposure="race",
outcome="force",
labels=c("race"="Minorité",
"suspicion"="Suspicion",
"force"="Usage de la force"))
#On récupère un ensemble de variables de conditionnement
conditionner<-data.table(dag_adjustment_sets(dag_race_force_simple)[[1]])
levels(factor(conditionner$set))## [1] "{(Backdoor Paths Unconditionally Closed)}"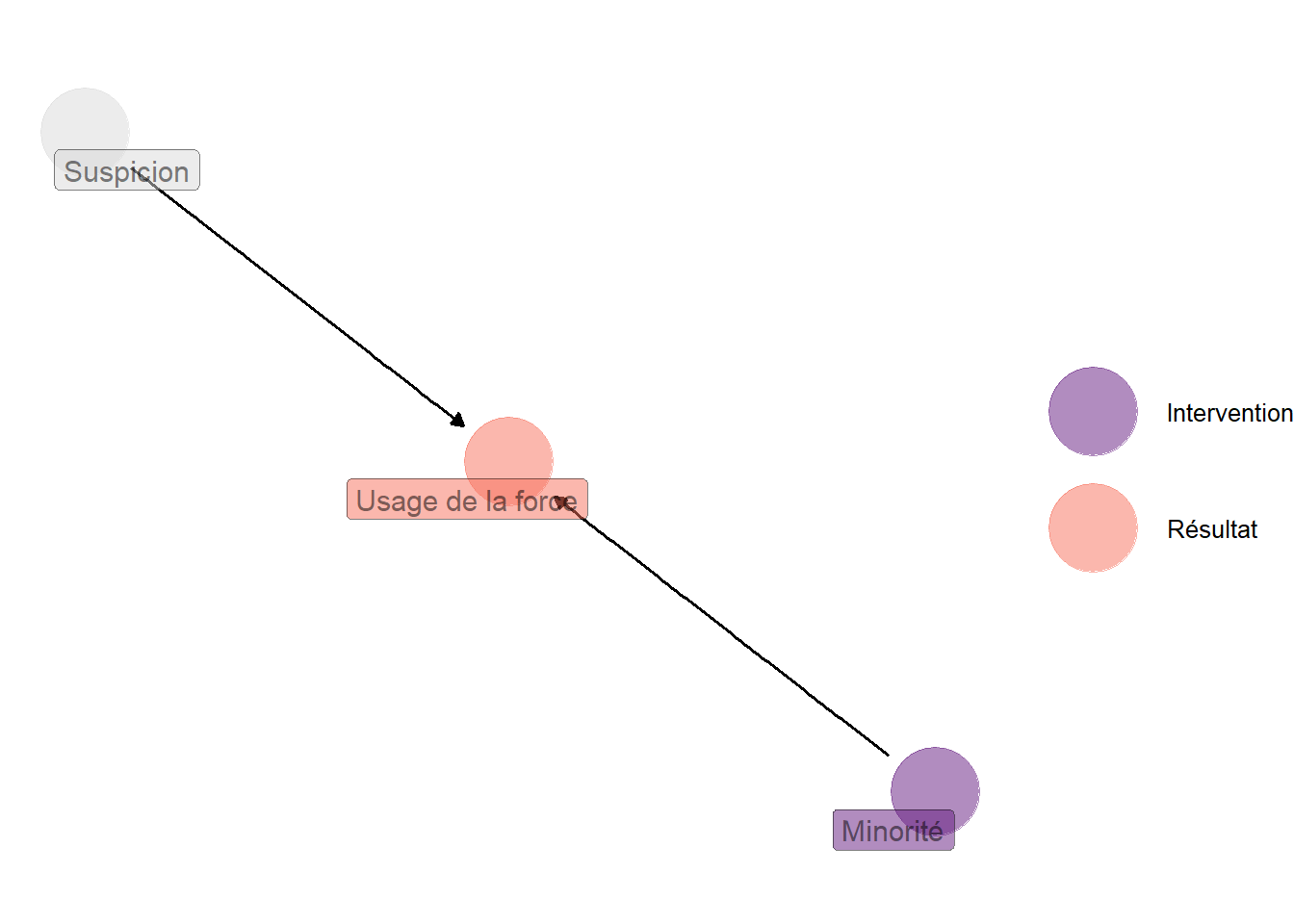
Figure 4.11: Représentation graphique inspirée de Knox, Lowe et Mummolo (2020). Dans ce cas, il est inutile de conditionner sur quelque variable que ce soit pour identifier les effets causaux moyens des biais racistes potentiels de la police étatsunienne sur son usage de la force.
Enfin la fonction dag_adjustment_sets est capable de repérer les cas où il n’existe pas de solution, c’est-à-dire où aucun choix d’ensemble de variables de conditionnement ne permet de bloquer les portes de sortie sans générer de biais. Le fragment de code suivant permet de générer un exemple fictif dans lequel aucune solution n’existe pour le problème.
library(ggdag)
dag_fict<-dagify(Y ~D + U2 +X,
D~U1,
X~U1+U2,
exposure = "D",
outcome = "Y",
latent = c("U1",
"U2"))
#On récupère un ensemble de variables de conditionnement
conditionner<-data.table(dag_adjustment_sets(dag_fict)[[1]])## Warning in dag_adjustment_sets(dag_fict): Failed to close backdoor paths. Common reasons include:
## * graph is not acyclic
## * backdoor paths are not closeable with given set of variables
## * necessary variables are unmeasured (latent)levels(factor(conditionner$set))## [1] "{(No Way to Block Backdoor Paths)}"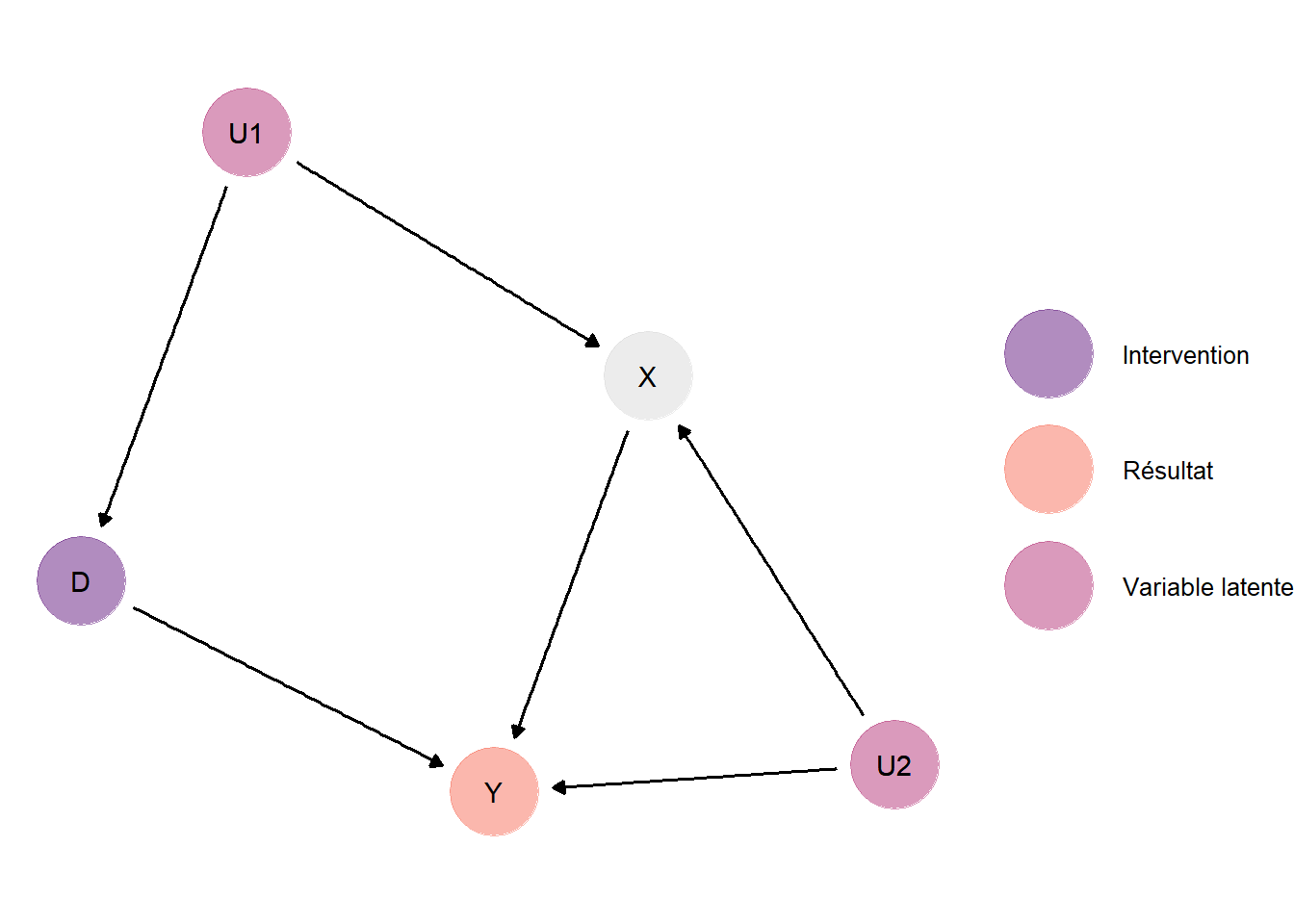
Figure 4.12: Représentation graphique d’une situation hypothétique où aucun ensemble de variables de conditionnement ne permet d’identifier des effets causaux moyens de l’intervention \(D\) sur le résultat \(Y\). En effet, il faudrait conditionner sur \(X\) pour fermer la porte de sortie \(D \longleftarrow U1 \longrightarrow X \longrightarrow Y\), mais conditionner sur \(X\) génère un biais de collision entre \(U1\) et \(U2\) à cause de la fourchette inversée \(U1 \longleftarrow X \longrightarrow U2\).