5.2 Fléau de la dimension et extrapolation

Lorsque l’on reste dans un cas simple, conditionner signifie simplement comparer la moyenne des individus ayant fait l’objet de l’intervention et de leurs homologues qui n’ont pas fait l’objet de l’intervention à l’intérieur de strates telles que tous ont les mêmes caractéristiques observables. Par exemple, lorsque l’on reprend comme Imai (2005) les données de l’expérience aléatoire contrôlée défectueuse de Gerber et Green (2000), en supposant que le seul problème est que la probabilité de recevoir un appel téléphonique varie d’un quartier de New Haven à l’autre, il suffit de toujours comparer des individus résidant dans le même quartier.

5.2.1 Le nombre de strates à considérer croît de façon exponentielle avec le nombre de variables de conditionnement (fléau de la dimension)

Dans ce qui précède, on a déjà fait abstraction d’une première difficulté : il y a un quartier au sein duquel aucune personne n’a reçu d’appel téléphonique ! De ce fait, les données ne peuvent pas renseigner sur l’effet causal moyen de l’appel téléphonique dans ce quartier, et donc, en toute rigueur, ne peut pas renseigner sur l’effet causal moyen à l’échelle de New Haven prise considérée dans son intégralité.

library(data.table)
library(ggplot2)
library(Matching)

#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)

GerberGreenImai[WARD=="22",
                list(effectif=.N),
                by=c("PHN.C1")]

##    PHN.C1 effectif
## 1:      0      281

On est pourtant encore là encore dans un cas simple où l’on n’utilise qu’une seule variable qualitative pour définir les strates au sein desquelles on regroupe les individus de la population. Imaginons un instant que l’on se trouve dans une situation dans laquelle il est nécessaire de conditionner sur 15 variables qualitatives. Il faut alors pouvoir définir \(2 \times 2^{15}=65536\) groupes différents, qui doivent tous être non-vides pour que l’on puisse calculer la moyenne de la participation électorale dans chacun d’entre eux. Cette valeur est relativement plus grande que le nombre de personnes interrogées dans l’enquête que l’on utilise ici (10829), et de façon générale plus grande que la plupart des échantillons dont on dispose dans les enquêtes statistiques usuelles¹⁵. Il serait ainsi certain que beaucoup de ces groupes ne pourraient pas être observés dans les données, et il serait de ce fait impossible d’estimer les effets causaux moyens de l’appel téléphonique sur la participation électorale.

De façon générale, il faut donc avoir en tête que chaque variable supplémentaire que l’on utilise pour conditionner, c’est-à-dire pour définir les strates au sein desquelles on peut faire les comparaisons pertinentes pour identifier les effets causaux moyens de l’intervention, double dans le meilleur des cas le nombre de strates. Autrement dit, le nombre de strates progresse beaucoup plus vite que le nombre de variables, et peut très rapidement dépasser le nombre d’observations dans les données dont on dispose. On appelle parfois cette croissance exponentielle du nombre de strates avec le nombre de variables fléau de la dimension. La figure suivante illustre cette croissance très rapide du nombre minimal de strates à considérer avec le nombre de variables de conditionnement

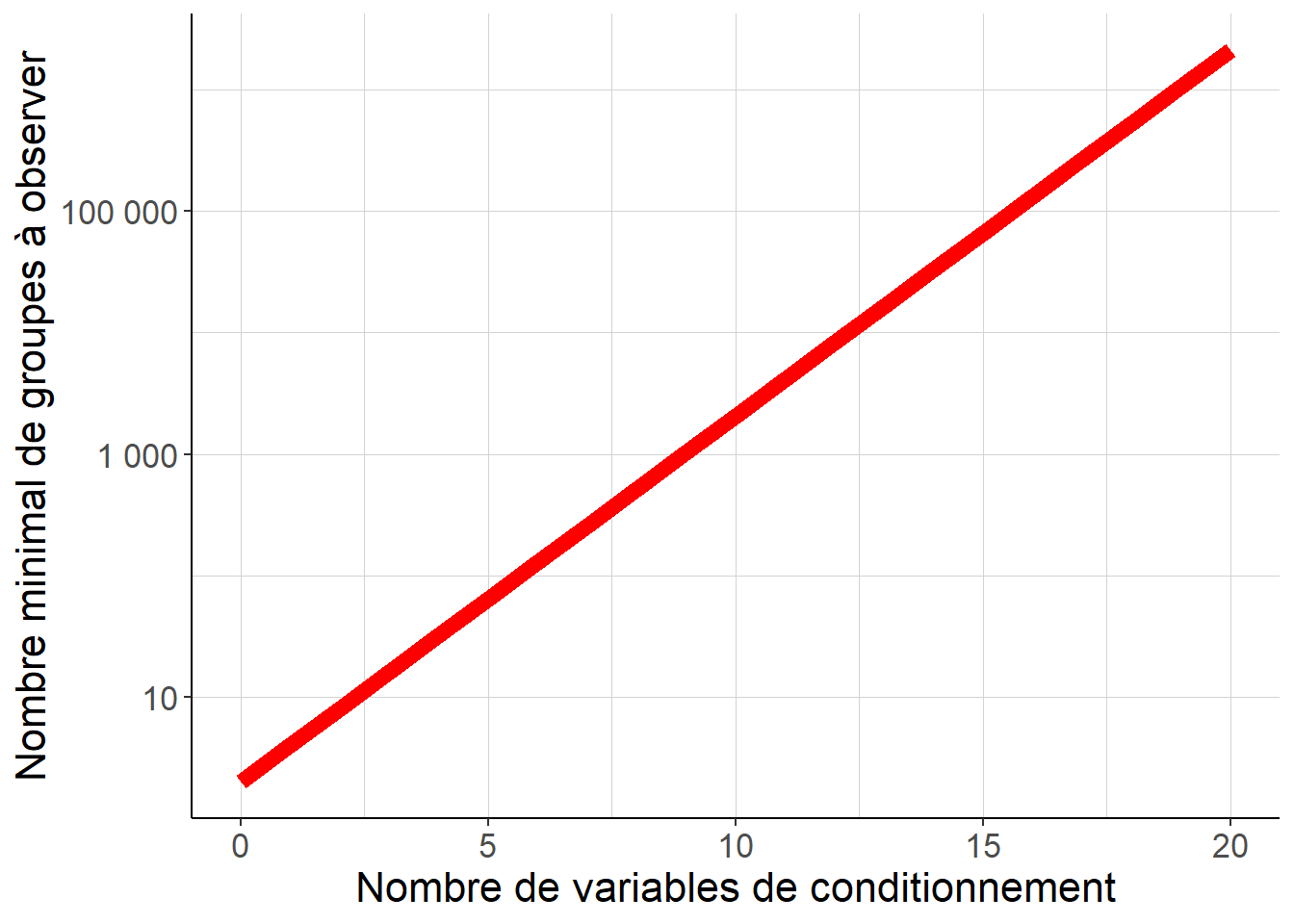
Figure 5.3: Le nombre minimal de groupes à oberver pour pouvoir faire la comparaison à l’intérieur de chaque strate augmente très rapidement avec le nombre de variables de conditionnement. De ce fait, plus on ajoute de variables, plus il est probable que l’on rencontre le cas de groupes vides, et donc qu’on ne puisse pas faire directement la comparaison à l’intérieur de chaque strate pertinente.

5.2.2 Les variables de conditionnement continues génèrent une infinité de groupes

Au-delà du problème du fléau de la dimension que l’on rencontre en multipliant les variables qualitatives, on rencontre également un problème proche pour les variables continues, par exemple le revenu. Au sen fort, conditionner sur le revenu revient à considérer une infinité, ou pour le moins un très grand nombre de très petite taille. En effet, lorsque l’on considère un ménage particulier, il est en général très improbable de trouver dans les données dont on dispose un autre ménage qui ait exactement le même revenu au centime près.

Le fragment de code suivant examine ce fait à partir des données de l’article de Dehejia et Wahba (1999), qui se veut une réévaluation des résultats de LaLonde (1986), consacré à l’évaluation du National Supported Work Demonstration (NSW), un programme d’emploi aidé temporaire qui a été expérimenté aux États-Unis à la fin des années 1970. Il suppose, pour les besoins de la démonstration, qu’il suffirait de conditionner sur le revenu du travail en 1974, avant l’entrée éventuelle dans le dispositif, pour identifier les effets causaux moyens du programme. Si cela paraît conceptuellement très simple, la pratique s’avère beaucoup plus compliquée : en effet, comme il est rare de trouver deux individus ayant exactement les mêmes revenus du travail au cent près, les strates définies par la variable sur laquelle on souhaite conditionner contiennent en général un seul individu observé, et donc dans ces strates observées, ou bien tout le monde est traité, ou bien personne ne l’est. Il est donc impossible d’y faire les comparaisons entre individus ayant bénéficié ou non du programme.

library(cobalt)
library(data.table)
library(ggplot2)

data("lalonde")
lalonde<-data.table(lalonde)

prob_traitement<-lalonde[,
                         list(prob_treat=mean(treat),
                              taille=.N),
                         by=c("re74")]

ggplot(data=prob_traitement,
       aes(x=re74,
           y=taille))+
  geom_point(alpha=0.5)+
  theme_classic()+
  xlab("Revenu en 1974 (en $)")+
  ylab("\nNombre d'individus observés")+
  theme(text=element_text(size=32),#taille du texte
        strip.text.x = element_text(size=32),
        legend.position="none",
        panel.grid.minor = element_line(colour="lightgray",
                                        size=0.01),#grille de lecture
        panel.grid.major = element_line(colour="lightgray",
                                        size=0.01))

ggplot(data=prob_traitement,
       aes(x=re74,
           y=prob_treat))+
  geom_point(aes(size=taille),
             alpha=0.5)+
  theme_classic()+
  scale_y_continuous(labels = scales::percent)+
  xlab("Revenu en 1974 (en $)")+
  ylab("Part des individus \nentrés dans le programme")+
  theme(text=element_text(size=32),#taille du texte
        strip.text.x = element_text(size=32),
        legend.position="none",
        panel.grid.minor = element_line(colour="lightgray",
                                        size=0.01),#grille de lecture
        panel.grid.major = element_line(colour="lightgray",
                                        size=0.01))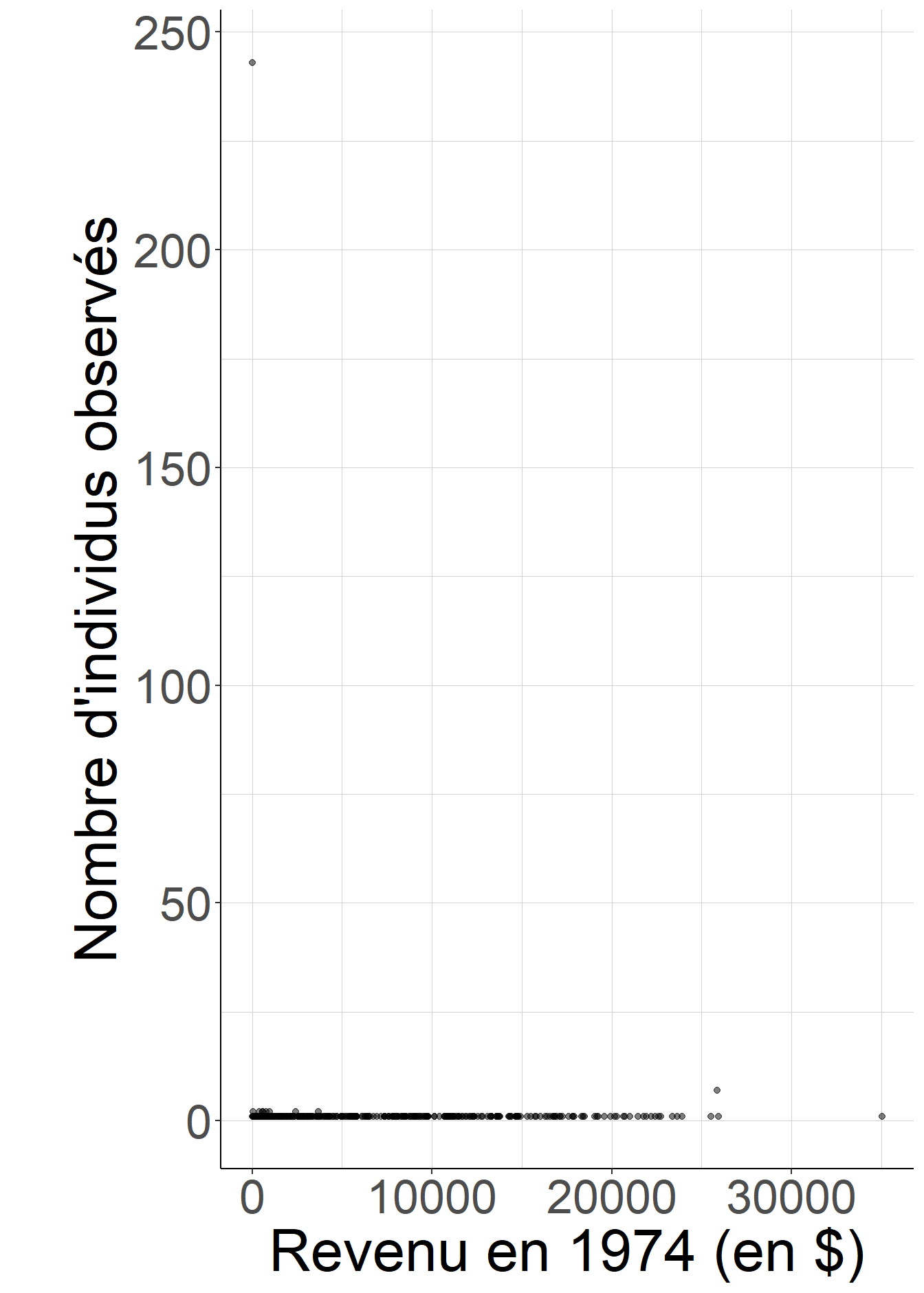

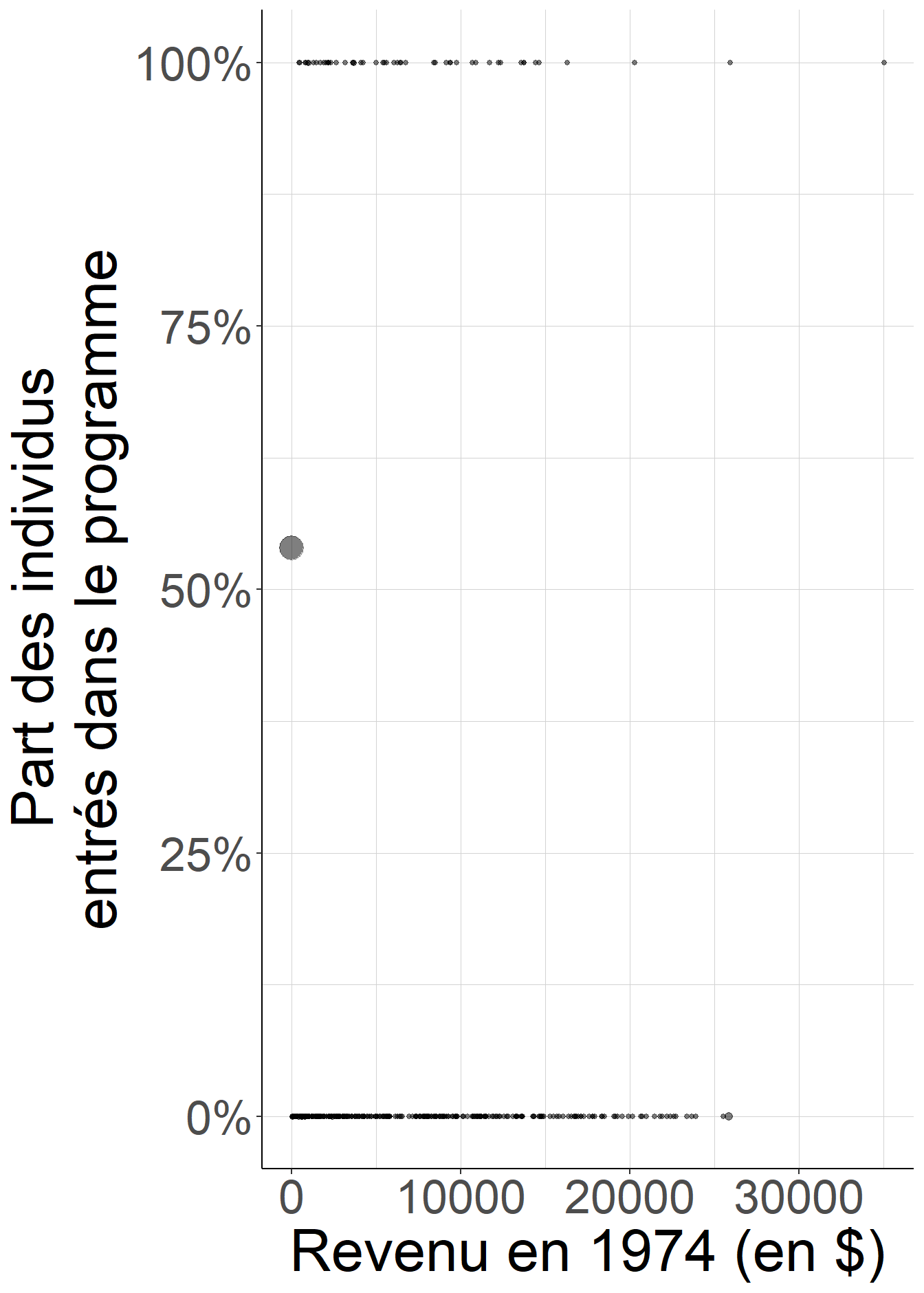
Figure 5.4: Lorsque l’on considère des groupes définis par le revenu du travail en 1974 au cent près, il est très rare de rencontrer deux individus ayant exactement le même revenu. De ce fait, dans presque toutes les strates définies par la valeur exacte du revenu de 1974, la part des individus ayant bénéficié du programme est ou bien 0, ou bien 1. Il n’est donc pas possible de comparer des individus ayant bénéficié ou non du programme dans ces strates.

5.2.3 Une nécessité : accepter d’extrapoler

L’approche naïve de stratification explicitée précédemment est donc en général impossible à employer directement dans la plupart des situations empiriques intéressantes : il est tout bonnement impossible d’observer dans la même strate définie par la valeur des variables de conditionnement \(X=x\) à la fois des individus qui ont fait l’objet de l’intervention, et des individus qui n’ont pas fait l’objet de l’intervention.

Cela ne signifie pas pour autant qu’il faille renoncer définitivement à identifier les effets de l’intervention que l’on souhaite étudier ! Simplement, il va falloir accepter une dose d’extrapolation à partir des données. En d’autres termes, il faut accepter d’utiliser les données d’une façon à obtenir, pour des valeurs des variables de conditionnement \(X=x\) pour lesquelles on n’observe que des individus ayant fait l’objet de l’intervention d’utiliser des données observées pour des valeurs voisines \(X=\tilde{x}\) pour construire une approximation raisonnable de la fréquence des individus non-observés n’ayant pas fait l’objet de l’intervention dans la strate \(X=x\) et du comportement que ces individus non-observés adoptent.

Le fragment de code suivant explicite ce à quoi vise cette extrapolation sur un extrait des données de Dehejia et Wahba (1999), en supposant toujours que l’ensemble des variables de conditionnement est réduit au revenu du travail observé en 1974. Conformément aux remarques précédentes, on observe dans la table obtenue à partir de la stratification naïve :

1. que l’effectif observé dans chaque strate est égal à 1 ;
2. que la probabilité observé de bénéficier du programme, c’est-à-dire la part d’individus ayant bénéficié du programme dans chaque strate est toujours égale à 0 ou 1 ;
3. que l’on n’observe jamais les valeurs du revenu du travail en 1978 que pour un seul des deux groupes possibles à l’intérieur de chaque strate.

Pourtant, lorsque l’on observe un individu ayant fait l’objet de l’intervention dont les revenus du travail en 1974 étaient 5424$, et un autre qui n’a pas bénéficié du programme et dont les revenus du travail en 1974 étaient 5454$, on a bien l’intuition que ce que l’on observe dans les données ne traduit pas très bien la réalité. En effet, la probabilité de bénéficier du programme ne passe probablement pas brusquement de 1 à 0 lorsque le revenu augmente de 19$, mais varie probablement plus continûment avec le revenu, et il en va de même pour les revenus du travail en 1978 selon que l’on n’a bénéficié ou pas du programme.

Cette intuition simple justifie d’utiliser l’information des individus qui ressemblent en un sens suffisamment les uns aux autres pour estimer les effets causaux moyens du programme. Pour le dire autrement, l’extrapolation consiste en quelque sorte à utiliser l’information des individus voisins pour :

1. remplacer les 0 et les 1 de la colonne prob_observ_treat par des valeurs plus crédibles de la probabilité de bénéficier du programme ;
2. remplacer les valeurs manquantes des colonnes revenu78_observe_traite et revenu78_observe_nontraite par des estimations raisonnables de ces revenus à partir des valeurs observées voisines.

Tout le reste de cette section est consacrée aux outils usuels qui permettent de mettre en place cette tentative d’extrapolation.

library(cobalt)
library(data.table)

data("lalonde")
lalonde<-data.table(lalonde)

table_extrapolation<-
  setorder(lalonde[,
                   list(effectif_observe=
                          .N,
                        prob_observ_treat=
                          sum(treat)/
                          .N,
                        revenu78_observe_traite=
                          sum(re78*treat)/
                          sum(treat),
                        revenu78_observe_nontraite=
                          sum(re78*(1-treat))/
                          sum(1-treat)),
                   by=c("re74")],
           re74)

table_extrapolation[re74>=5000
                    & re74<=6000]

##         re74 effectif_observe prob_observ_treat revenu78_observe_traite
##  1: 5005.731                1                 1               5615.1890
##  2: 5023.560                1                 0                     NaN
##  3: 5099.971                1                 0                     NaN
##  4: 5229.283                1                 0                     NaN
##  5: 5260.631                1                 0                     NaN
##  6: 5374.269                1                 0                     NaN
##  7: 5424.485                1                 1               6788.4630
##  8: 5454.599                1                 0                     NaN
##  9: 5460.477                1                 0                     NaN
## 10: 5506.308                1                 1                671.3318
## 11: 5523.173                1                 0                     NaN
## 12: 5597.625                1                 0                     NaN
## 13: 5605.852                1                 1                  0.0000
## 14: 5607.422                1                 0                     NaN
## 15: 5683.833                1                 0                     NaN
## 16: 5699.507                1                 0                     NaN
## 17: 5777.878                1                 0                     NaN
## 18: 5797.470                1                 0                     NaN
## 19: 5817.063                1                 0                     NaN
## 20: 5822.941                1                 0                     NaN
##     revenu78_observe_nontraite
##  1:                        NaN
##  2:                  6756.1660
##  3:                 12718.7900
##  4:                 15892.9500
##  5:                  9253.5240
##  6:                     0.0000
##  7:                        NaN
##  8:                     0.0000
##  9:                  7539.3610
## 10:                        NaN
## 11:                  5040.5250
## 12:                   122.6513
## 13:                        NaN
## 14:                    94.5745
## 15:                  4742.0250
## 16:                  8844.1940
## 17:                   135.9508
## 18:                  2160.4360
## 19:                  1066.9190
## 20:                 11075.5600

---

15. L’échantillon de l’Enquête Emploi en Continu (EEC) réalisée par l’Insee, qui généralement considérée comme une enquête avec un grand échantillon, est d’environ 92000 logements.↩︎