5.3 Notion de score de propension

Extrapoler consiste essentiellement à essayer d’utiliser de l’information issue de strates proches mais différentes pour pallier au problème qui découle du fait que lorsque les strates théoriquement pertinentes deviennent très fines, dans la plupart d’entre elles, travailler sur un échantillon de taille finie conduit à n’observer ou bien que des individus ayant fait l’objet de l’intervention, ou bien seulement des individus qui n’ont pas fait l’objet de l’intervention.

L’usage du score de propension est en premier lieu de permettre de définir des strates plus grandes, et donc dont il est moins probable qu’elles soient vides, telles que l’assimilation de la situation empirique à une expérience aléatoire contrôlée ou à une expérience naturelle soit encore valable. En fait, il est possible de montrer que les strates définies par le score de propension sont les plus grandes possibles telles que cette assimilation soit valable.

On peut faire l’expérience de pensée suivante, en revenant à l’exemple de l’effet de l’appel téléphonique sur la participation électorale de Gerber et Green (2000) et Imai (2005), et en supposant une fois encore que la seule erreur dans la randomisation tient à ce que les habitants de certains quartiers de New Haven ont reçu davantage d’appels téléphoniques que d’autres. Supposons que l’on considère deux quartiers pour lesquels la probabilité de faire l’objet d’un appel était la même, par exemple 2.5%. Cela signifie qu’à l’intérieur de chacun de ces quartiers considéré séparément, on peut assimiler la situation empirique à une expérience aléatoire contrôlée avec une probabilité de faire l’objet de l’intervention égale à 2.5%.

Mais cela vaut tout autant pour les deux quartiers réunis ! Ainsi, on peut considérer qu’au lieu de regarder deux expérience aléatoires contrôlées séparées avec un probabilité de recevoir un appel de 2.5%, on regarde en fait une seule grande expérience aléatoire contrôlée avec la même probabilité de recevoir un appel. La figure 5.5 illustre cette idée.

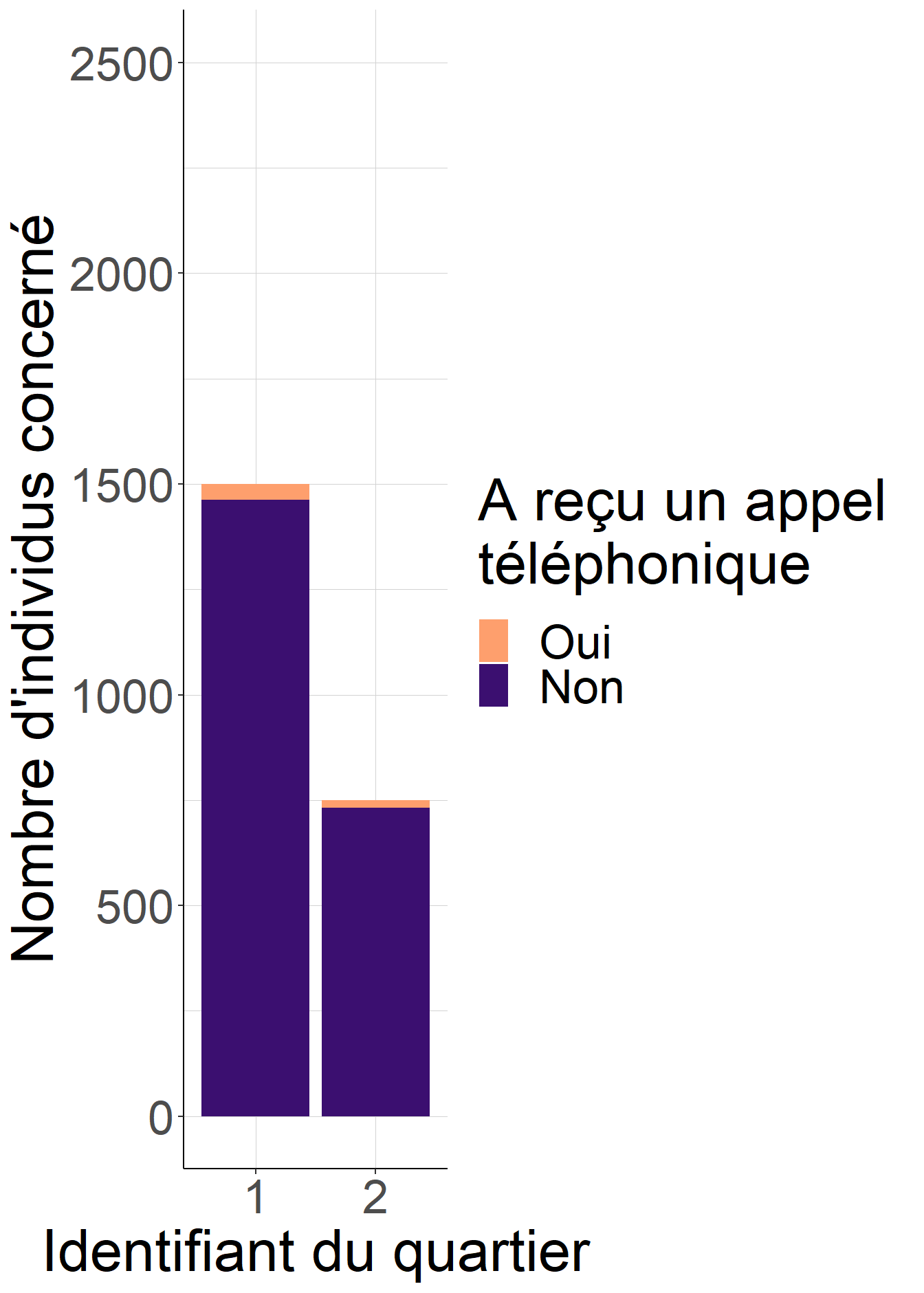
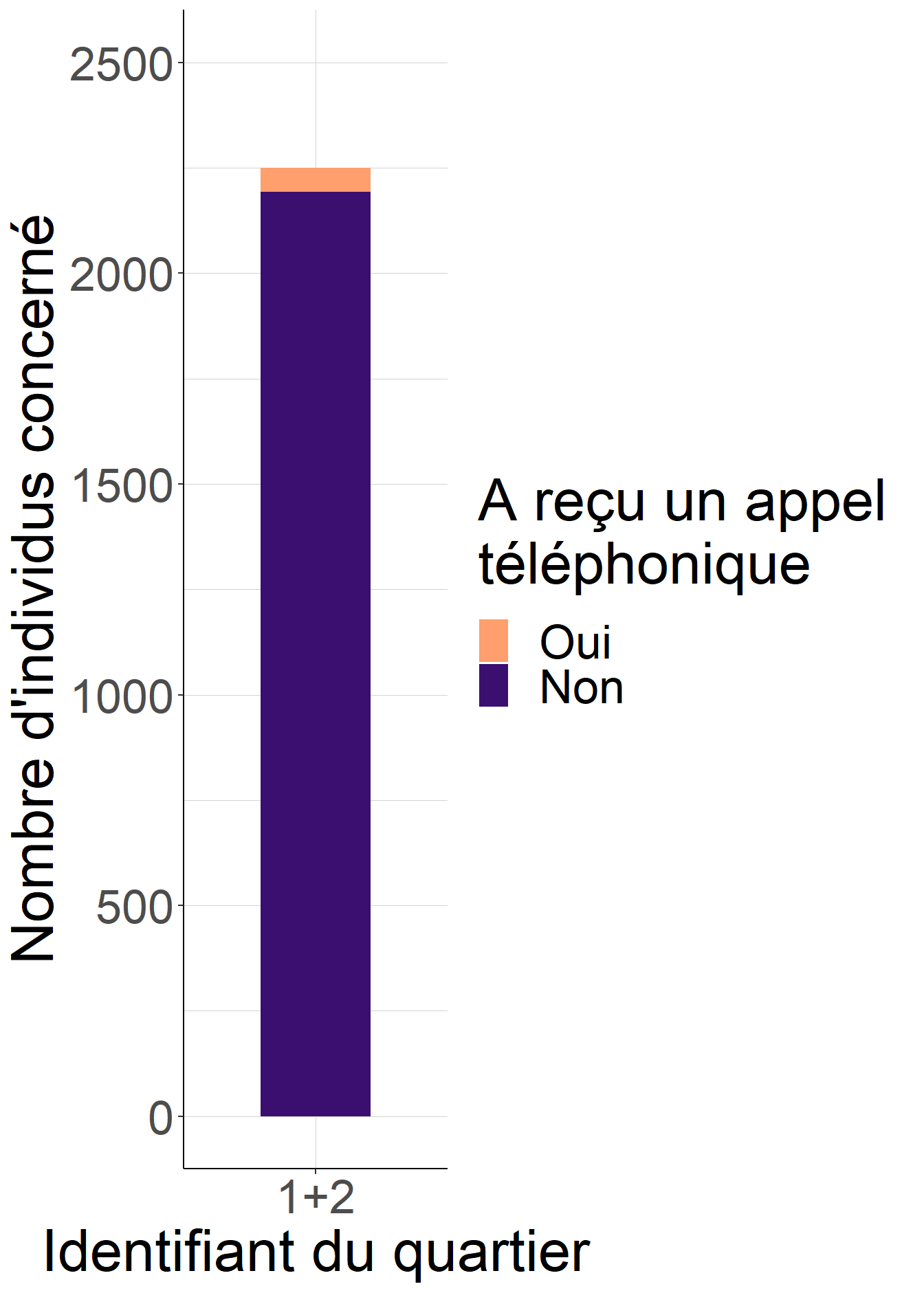
Figure 5.5: La probabilité de recevoir un appel téléphonique lors de l’expérience aléatoire contrôlée ratée est la même dans les deux quartiers, égale à 2.5%. Au lieu de considérer chaque quartier comme une expérience aléatoire contrôlée effectuée séparément, on peut considérer la réunion des deux quartiers comme une seule grande expérience aléatoire contrôlée avec une probabilité de recevoir un appel égale à 2.5%.

Cette idée a bien entendu une valeur plus générale.

Définition

Le score de propension est la probabilité conditionnelle de faire l’objet de l’intervention, ou en d’autres termes la part, parmi les individus de la population d’intérêt (et pas seulement de l’échantillon) dont les variables de conditionnement prennent la valeur (multidimensionnelle) \(x\), de ceux qui font l’objet de l’intervention : \(p(x):=\mathbb{P}(D_i=1\mid X_i=x)\).

L’usage du score de propension repose sur une généralisation de l’idée simple mais essentielle introduite plus haut : il est possible d’utiliser le score de propension pour définir des strates plus grandes que celles définies par les valeurs des variables de conditionnement, au sein desquelles l’assimilation de la situation empirique à une expérience aléatoire contrôlée, ou à une expérience naturelle, est encore légitime.

À retenir

Si les variables de conditionnement permettent de définir des strates au sein desquelles la situation empirique est assimilable à une expérience aléatoire contrôlée, ou à une expérience naturelle, alors le score de propension permet de définir des strates plus grandes au sein desquelles cette assimilation est toujours valable. Ainsi, à l’intérieur de ces grandes strates, les valeurs potentielles de la variable d’intérêt ne dépendent pas de l’assignation à l’intervention, de sorte que la comparaison des individus ayant fait l’objet de l’intervention avec ceux qui n’en ont pas fait l’objet permet d’identifier les effets causaux moyens de celle-ci. De plus, la distribution des caractéristiques observables définies par les variables de conditionnement est la même dans chacun de ces groupes lorsque l’on fait la comparaison à l’intérieur d’une grande strate définie par le score de propension.

Formellement, ce résultat consiste à dire que si l’hypothèse d’indépendance conditionnelle tient, c’est-à-dire si l’assignation à l’intervention est indépendante des valeurs potentielles de la variable d’intérêt à l’intérieur de strates définies par les valeurs prises par caractéristiques observables, alors cette hypothèse d’indépendance conditionnelle tient encore à l’intérieure de strates définies par les valeurs du score de propension. De plus, à l’intérieur des strates définies par le score de propension, et pour la même raison, les caractéristiques observables décrites par les variables de conditionnement sont indépendantes de l’assignation à l’intervention :

\[\left\{\begin{array}{l} (Y_i(1),\, Y_i(0)) \perp \!\!\! \perp D_i \mid p(X_i) \\ X_i \perp \!\!\! \perp D_i \mid p(X_i) \\ \end{array} \right.\]

La lectrice ou le lecteur intéressé trouvera en Annexe A.14 une preuve de ce résultat dû à Rosenbaum et Rubin (1983), que l’on désigne en général sous le nom de propriété équilibrante du score de propension.