5.5 Estimation du score de propension
Le score de propension est un outil précieux dans l’estimation des effets causaux moyens de l’intervention, en ceci qu’il permet de définir les plus grandes strates possibles au sein desquelles l’assimilation de la situation empirique à une expérience aléatoire contrôlée ou à une expérience naturelle est valable. Le problème que l’on rencontre toutefois dans la plupart des cas est que, contrairement au cas idéal de l’expérience aléatoire stratifiée pour laquelle l’expérimentateur connaît les probabilités utilisées pour assigner l’intervention dans les différentes strates, le score de propension n’est en général pas connu !
Il n’est par conséquent pas possible de s’appuyer sur directement sur le score de propension à proprement parler pour définir les strates au sein desquelles faire la comparaison entre les individus ayant fait l’objet de l’intervention et ceux qui n’en ont pas fait l’objet. Pour pouvoir exploiter les propriétés du score de propension, il est nécessaire de passer par une étape préalable : il faut l’estimer à partir des données dont on dispose.
5.5.1 Problèmes de l’estimation naïve
Une première approche, qui semble particulièrement naturelle, pour estimer le score de propension serait d’utiliser la part des individus de l’échantillon qui font l’objet de l’intervention dans chacune des strates définies par la valeur des variables de conditionnement. Cette idée séduisante est cependant erronée pour deux raisons.
5.5.1.1 L’estimation naïve du score de propension est inutilisable dans les situations qui justifient le passage par le score de propension
La première raison est la plus simple : dans l’essentiel des cas qui motivent le passage par le score de propension, cette estimation naïve est infaisable. En effet, si l’on cherche à estimer le score de propension, c’est avant tout parce que les strates trop fines définies par les valeurs des variables de conditionnement ne permettent d’observer, dans chacune d’entre elles, qu’un tout petit nombre d’individus, souvent un seul, et donc seulement des individus ayant fait l’objet de l’intervention, ou bien seulement des individus n’ayant pas fait l’objet de l’intervention.
Le fragment de code suivant met ce fait en évidence à partir de l’exemple des données de Dehejia et Wahba (1999). Cette fois encore, on considère l’évaluation du NSW, en supposant toujours pour les besoins de la démonstration que conditionner par les revenus du travail en 1974 serait suffisant pour identifier les effets causaux moyens de ce programme.
Considérer l’estimation naïve du score de propension plutôt que les valeurs des revenus du travail permet d’abaisser le nombre de strates à considérer de 358 à 3. Il semble donc bien que l’on gagne ainsi des strates beaucoup plus grosses que celles que l’on envisageait initialement. Cela étant, force est de constater que parmi ces 3 grosses strates, deux sont inutilisables : ce sont les strates définies par le niveau de l’estimation naïve du score de propension égale à 0 ou 1. En effet, dans ces strates par définition la comparaison nécessaire à l’estimation de l’effet causal moyen du programme est impossible. De plus, la grosse strate restante est en fait strictement équivalente à une strate définie directement à partir des revenus du travail observés en 1974 : c’est la strate de ceux dont le revenu du travail en 1974 est nul.
L’estimation naïve du score de propension est donc en définitive inutilisable ici : les seules strates qu’elle permet d’agréger ensemble sont des strates pour lesquelles la comparaison est infaisable, et les strates définies par cette estimation pour lesquelles la comparaison est faisable pouvaient déjà être construites à partir des revenus du travail observés en 1974.
library(cobalt)
library(data.table)
data("lalonde")
lalonde<-data.table(lalonde)
prob_traitement<-lalonde[,
list(score_propension_naif=mean(treat),
taille=.N),
by=c("re74")]
nrow(prob_traitement)## [1] 358strate_score_propension_naif<-setorder(prob_traitement[,
list(taille=sum(taille),
min_re74=min(re74),
max_re74=max(re74),
nbr_strates_init=.N),
by=c("score_propension_naif")],
taille)
strate_score_propension_naif## score_propension_naif taille min_re74 max_re74 nbr_strates_init
## 1: 1.0000000 54 445.17040 35040.07 52
## 2: 0.5390947 243 0.00000 0.00 1
## 3: 0.0000000 317 33.30754 25862.32 3055.5.1.2 Lorsqu’elle est utilisable, l’estimation naïve du propension conduit à des résultats exactement équivalents à ceux que l’on obtient en utilisant les strates définies par les variables de conditionnement
L’exemple précédent montre que dans le cas des variables continues, qui motive en partie l’usage du score de propension plutôt que le conditionnement direct, l’estimation naïve du score de propension est essentiellement inutilisable. La question qui peut alors se poser est de savoir comment cette estimation se comporte dans les cas où elle est utilisable.
Pour examiner ce problème, on peut revenir à l’exemple de Gerber et Green (2000) et Imai (2005), en faisant toujours l’hypothèse très simplificatrice que le seul problème qui s’est posé lors de l’expérience aléatoire contrôlée est que la probabilité de recevoir un appel différait d’un quartier à l’autre de New Haven. Le fragment de code suivant permet de vérifier que dans ce cas, on obtient exactement les mêmes résultats en passant par l’estimation directe des effets causaux moyens du traitement ou en passant par l’estimation naïve du score de propension.
library(data.table)
library(Matching)
#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)
#On estime la probabilité d'avoir reçu un appel téléphonique pour chaque
# quartier de New Haven, c'est-à-dire le score de propension,
# ainsi que la participation électorale de chaque quartier, pour
# chaque groupe séparément
stat_niveau_quartier<-GerberGreenImai[,
list(score_propension=mean(PHN.C1),
taille=.N,
prob_vote_appel=sum(VOTED98*PHN.C1)/
sum(PHN.C1),
prob_vote_sans_appel=sum(VOTED98*(1-PHN.C1))/
sum(1-PHN.C1)),
by=c("WARD")]
#Estimation directe sans passer par le score de propension
# Comme à l'intérieur de chaque quartier, on suppose que la randomisation est
# correcte, on peut en tirer un effet moyen spécifique à chaque quartier
stat_niveau_quartier[,
effet_moyen:=prob_vote_appel-prob_vote_sans_appel]
#L'effet causal moyen sur tout New Haven est la moyenne des effets moyens dans
# chaque quartier (quand on pondère par la taille du quartier)
ATE_estimation_directe<-stat_niveau_quartier[!is.na(effet_moyen),
sum(effet_moyen*taille)/
sum(taille)]
#Estimation en définissant les grandes strates à partir du
# score de propension estimé de façon naïve
stat_strates_score_propension_naif<-
stat_niveau_quartier[,
list(taille=sum(taille),
nbr_quartiers=.N,
prob_vote_appel=sum(taille*prob_vote_appel)/
sum(taille),
prob_vote_sans_appel=
sum(taille*prob_vote_sans_appel)/
sum(taille)),
by=c("score_propension")]
#A l'intérieur des strates définies par le score de propension, la situation est
# assimilable à une expérience aléatoire contrôlée, donc il suffit de calculer
# la différence entre les taux de participation
stat_strates_score_propension_naif[,
effet_moyen:=prob_vote_appel-
prob_vote_sans_appel]
#Il ne reste plus qu'à réagréger les différentes strates entre elles,
# avec des poids proportionnels à leur taille dans la population de
# New Haven
ATE_estimation_score_propension_naif<-
stat_strates_score_propension_naif[!is.na(effet_moyen),
sum(effet_moyen*taille)/
sum(taille)]
#On vérifie finalement que les deux stratégies conduisent exactement
# au même résultat
all.equal(ATE_estimation_directe,
ATE_estimation_score_propension_naif)## [1] TRUEEn fait, les deux exemples précédents qui montrent les limites de l’usage naïf du score de propension tiennent à ce que, tout en espérant des gains liés à l’utilisation de cet outil, on n’a pas encore réellement accepté la nécessité de l’extrapolation, et en particulier la nécessité de se doter d’un concept de proximité entre observations ou entre strates :
- Dans l’exemple construit à partir de Dehejia et Wahba (1999), on n’accepte pas de faire appel à un concept de proximité entre revenus du travail observés en 1974, ce qui conduit à traiter totalement indépendamment des autres chaque niveau de revenu. Ainsi, l’estimation naïve suppose qu’il n’y a pas plus de rapport entre les individus dont les revenus du travail en 1974 étaient 5424$ et ceux dont les revenus étaient 5443$ qu’entre les premiers et ceux dont les revenus du travail en 1974 étaient nuls.
- Dans l’exemple construit à partir de Gerber et Green (2000), on ne considère que des strates définies par la valeur exacte du score de propension estimé, et l’on n’utilise donc pas de concept de proximité entre scores de propension. En fait, comme les part exactes d’individus ayant reçu un appel téléphonique diffèrent toujours d’un quartier à l’autre, passer par le score de propension génère exactement les mêmes strates que lorsque l’on fait l’estimation directe.
En somme, l’utilisation naïve du score de propension est en un sens incohérente avec elle-même, parce qu’en refusant de se confronter à la nécessité d’extrapoler et de se doter de concepts de proximité entre observations et entre strates, elle contredit les idées qui motivent l’introduction du concept de score de propension.
5.5.2 En pratique
Il est donc nécessaire d’accepter une utilisation du score de propension qui prenne sérieusement en compte la nécessité d’extrapoler, et qui permette de faire appel à un ou des concepts de proximité entre observations ou entre strates.
Du côté de l’estimation du score de propension, cela passe souvent par le passage par des modèles paramétriques. Formellement, ce passage par des modèles paramétriques signifie qu’au lieu de supposer une dépendance la plus générale possible entre les valeurs des variables de conditionnement et le score de propension, on fait l’hypothèse que celle-ci doit être recherchée dans un ensemble beaucoup plus petit de fonctions, que l’on peut écrire sous la forme \(p(x)=f(x'\beta)\), où \(f\) est une fonction connue et définie a priori et \(\beta\) un vecteur de même dimension que les variables de conditionnement16. Les modèles logit et probit sont deux exemples particulièrement fréquents de tels modèles, qui se distinguent par le choix de la fonction \(f\), que l’on appelle parfois fonction de lien.
Tout le problème est alors de choisir :
- une fonction de lien \(f\) appropriée au problème considéré, et ;
- ce que l’on appelle parfois une spécification, c’est-à-dire une façon de faire entrer l’information potentiellement très riche contenue dans les variables de conditionnement dans une variable de dimension finie, par exemple en incluant ou pas des interactions ou des termes polynomiaux d’ordre supérieur à 1, en considérant le logarithme de certaines variables plutôt que leur niveau brut etc.
Schématiquement, il faut naviguer entre deux écueils :
- autoriser une spécification trop souple, qui conduise à retomber dans les problèmes rencontrés avec l’estimation naïve du score de propension ;
- imposer une spécification trop rigide et trop simple, qui conduise à s’éloigner de façon trop marquée de la réalité en imposant un grand nombre d’hypothèses supplémentaires injustifiées.
5.5.2.1 Un cas particulier important : le cas de la régression saturée
Pour comprendre le premier écueil, on peut revenir à l’exemple de Gerber et Green (2000), toujours en faisant l’hypothèse que conditionner par le quartier permet de résoudre les problèmes posés par la mauvaise randomisation au cours de l’expérience aléatoire contrôlée. Sur cet exemple, on peut considérer le choix de plusieurs fonctions de lien, et comparer les scores de propension obtenus au score de propension estimé de façon naïve. Le fragment de code suivant permet de faire cette comparaison.
library(data.table)
library(Matching)
#On récupère les données et on convertit en data.table
data(GerberGreenImai)
GerberGreenImai<-data.table(GerberGreenImai)
#On estime la probabilité d'avoir reçu un appel téléphonique pour chaque
# quartier de New Haven, c'est-à-dire le score de propension
# avec l'estimateur naïf
stat_niveau_quartier<-GerberGreenImai[,
list(score_propension_naif=mean(PHN.C1)),
by=c("WARD")]
#On remet ça avec les données initiales
GerberGreenImai<-merge(GerberGreenImai,
stat_niveau_quartier,
by=c("WARD"))
#On fait la même estimation avec un logit, et on récupère
# les probabilités prédites, c'est-à-dire l'estimation du score
# de propension
logit_propensity_score<-glm(PHN.C1 ~ WARD,
data=GerberGreenImai,
family = binomial(link = logit))$fitted.values
#On fait la même estimation avec un probit, et on récupère
# les probabilités prédites, c'est-à-dire l'estimation du score
# de propension
probit_propensity_score<-glm(PHN.C1 ~ WARD,
data=GerberGreenImai,
family = binomial(link = probit))$fitted.values
#On fait la même estimation avec un cauchit, et on récupère
# les probabilités prédites, c'est-à-dire l'estimation du score
# de propension
cauchit_propensity_score<-glm(PHN.C1 ~ WARD,
data=GerberGreenImai,
family = binomial(link = cauchit))$fitted.values
#On peut encore faire la même chose avec une régression linéaire, comme la
# variable dépendante est dichotomique, l'espérance conditionnelle est égale
# à la probabilité conditionnelle qu'elle vaille 1, c'est-à-dire que la
# valeur prédite est une estimation du score de propension
MCO_propensity_score<-lm(PHN.C1 ~ WARD,
data=GerberGreenImai)$fitted.values
#On regroupe ces quatre estimations avec les données initiales
GerberGreenImai<-cbind(GerberGreenImai,
logit_propensity_score,
probit_propensity_score,
cauchit_propensity_score,
MCO_propensity_score)
#On vérifie que les quatre estimations sont égales entre elles
all.equal(logit_propensity_score,
probit_propensity_score)## [1] TRUEall.equal(logit_propensity_score,
cauchit_propensity_score)## [1] TRUEall.equal(logit_propensity_score,
MCO_propensity_score,
tolerance=1e-7)## [1] TRUE#Pour les MCO il faut autoriser des très légères différences qui tiennent à la
# façon dont glm procède à l'estimation
#On vérifie que ces estimations sont égales à l'estimation
# naïve du score de propension
#L'erreur ne tient qu'à certaines approximations inhérentes
# à l'estimation par glm
all.equal(GerberGreenImai$score_propension_naif,
GerberGreenImai$logit_propensity_score,
tolerance=1e-7)## [1] TRUECe résultat a bien entendu une valeur plus générale.
À retenir
Lorsque l’on cherche à estimer le score de propension avec un modèle paramétrique, quelque soit la fonction de lien choisie, considérer un modèle saturé, c’est-à-dire un modèle où les variables indépendantes sont des variables dichotomiques qui décrivent des strates (i) mutuellement exclusives et (ii) qui recouvrent tout l’espace des possibles renvoie les mêmes résultats que l’estimation naïve du score de propension par la part observée d’individus ayant fait l’objet de l’intervention dans chaque strate.
5.5.2.2 Un exemple avec une variable de conditionnement continue
Le fragment de code suivant examine le problème du choix de spécification et de fonction de lien dans le cas des variables continues. Il revient sur l’exemple de Dehejia et Wahba (1999), en supposant toujours pour les besoins de la démonstration qu’il suffit de conditionner par les revenus du travail observés en 1974 pour identifier les effets causaux moyens de la participation au NSW. Pour étudier les effets potentiels du choix de spécification et de fonction de lien, on se propose de se pencher sur 4 fonctions de lien classiques : probit, logit, cauchit, et enfin une fonction de lien gaussienne qui revient à avoir recours à la méthode des moindres carrés ordinaires.
On compare les résultats obtenus avec ces différentes fonctions de lien entre elles d’une part, en s’intéressant à la corrélation entre les scores de propension estimés avec chacune d’entre elles, et d’autre part à une approche beaucoup plus flexible, que l’on pourrait dire non-paramétrique, qui consiste à ranger les observations en des pseudos-strates de taille fixée à l’avance en regroupant entre eux les individus dont les revenus observés en 1974 sont les plus proches, puis à estimer le score de propension en considérant ou bien (i) la part des individus qui entrent dans le programme pour chacune de ces pseudo-strates, ou bien (ii) les probabilités prédites par une régression linéaire effectuée séparément dans chacune de ces pseudo-strates.
On fait de plus ces comparaisons :
- d’une part, pour la spécification la plus simple possible, qui ne considère qu’un seul terme linéaire en revenus du travail observés en 1974, et ;
- d’autre part avec une spécfication légèrement plus flexible qui permet de surcroît de distinguer les individus dont les revenus du travail étaient nuls en 1974 des autres.
Les résultats de ces comparaisons sont instructifs. Avec la spécification la plus simple, le choix de fonction de lien peut conduire à des estimations assez différentes du score de propension, et peut s’éloigner de façon non-négligeable de ce que l’on observe dans les données dés lors que l’on se permet une grande flexibilité. Ainsi, lorsque seul un terme linéaire en revenus du travail de 1974 est considéré, la corrélation entre le score de propension estimé, quelque soit la fonction de lien retenue, et les estimations non-paramétriques est relativement faible. En d’autres termes, avoir introduit trop de rigidité dans l’estimation conduit à des valeurs estimées du score de propension qui peuvent s’éloigner de façon problématique de ses valeurs réelles.
Lorsque l’on s’autorise en revanche un tout petit peu plus de flexibilité, les scores de propensions estimés sont pratiquement les mêmes quel que soit le choix de fonction de lien, et leur valeurs sont extrêmement proches de celles obtenus par une approche non-paramétrique. Ainsi, dans ce cas, le choix de fonction de lien ne joue plus aucun rôle, et la très grand proximité avec l’estimation non-paramétrique suggère que l’on ne gagnerait pas grand chose à considérer une spécification plus riche.
Si la littérature peut orienter vers des pratiques meilleures que d’autres, aucune règle générale très claire ne se dégage quant au choix de spécification et de fonction de lien dans l’estimation paramétrique du score de propension. Ce qu’il faut rechercher, plus que le choix parfait, c’est le choix robuste et cohérent avec la théorie sociologique de l’objet que l’on aborde. En d’autres termes, si pour la spécification retenue, le choix de fonction de lien change de façon non-négligeable les valeurs estimées du score de propension, et donc les effets estimés des effets causaux moyens, et si l’on ne dispose pas d’une théorie spécifique à l’objet qui justifie un choix plutôt qu’un autre, il ne faut pas penser que l’on va disposer d’un argument statistique permettant de privilégier une option plutôt qu’une autre. En réalité, cette variabilité des résultats en fonction du choix de fonction de lien jette le doute sur tous les résultats obtenus à partir de cette spécification, quelle que soit la fonction de lien retenue.
library(cobalt)
library(data.table)
library(ggplot2)
library(viridis)
#On récupère les données
data("lalonde")
lalonde<-data.table(lalonde)
#On crée la variable qui indique des revenus du travail nul en 1974
lalonde[,
u74:=as.numeric(re74==0)]
#Fonction qui renvoie les probabilités prédites d'entrée dans le programme
# pour chaque observation, pour un choix de spécification et une
# fonction de lien dans un modèle dichotomique
estimationparamdichot<-function(specification,
link_function){
glm(as.formula(paste0("treat ~",
specification)),
data = lalonde,
family = binomial(link = link_function))$fitted.values
}
#Fonction qui renvoie les probabilités prédites d'entrée dans le programme
# pour chaque observation, pour un choix de spécification et une estimation
# par les moindres carrés ordinaires
estimationparamMCO<-function(specification){
lm(as.formula(paste0("treat ~",
specification)),
data=lalonde)$fitted.values
}
#Tentative d'estimation non-paramétrique : on regroupe les observations par
# pseudostrates de taille minimale définie (en nombre d'observations) et on
# calcule la part des individus entrés dans le programme à l'intérieur de
# chacune de ces strates
estimationnonparam<-function(taillepseudostrate,
specificationNP){
#On récupère le nombre d'individus observés pour chaque niveau de revenu
re74groups_lalonde<-setorder(lalonde[,
list(nb_indiv=.N),
by=c("re74")],
re74)
#On associe à chaque niveau de revenu une pseudostrate en première intention
# en faisant des groupes de taille au moins pseudokernel en partant de 0
re74groups_lalonde[,
nb_cumul_indiv:=cumsum(nb_indiv)]
re74groups_lalonde[,
re74group:=floor(nb_cumul_indiv/
taillepseudostrate)*
taillepseudostrate]
#Il faut faire attention car la dernière pseudostrate est potentiellement
# toute petite ! On la réagrège avec l'avant dernière
derniergroupe=max(re74groups_lalonde$re74group)
if(max(re74groups_lalonde[re74group==derniergroupe]$nb_cumul_indiv-
derniergroupe)<=taillepseudostrate)
{
avantderniergroupe<-
max(re74groups_lalonde[re74group!=derniergroupe]$re74group)
re74groups_lalonde[re74group==derniergroupe,
re74group:=avantderniergroupe]
}
#Il faut aussi mettre le groupe des 0 à part
re74groups_lalonde[re74==0,
re74group:=0]
#On peut remettre chaque individu dans son groupe
lalondedat<-merge(lalonde[,
c("re74",
"treat")],
re74groups_lalonde[,
c("re74",
"re74group")],
by=c("re74"))
#Dans chaque groupe on estime un modèle de probabilité linéaire et on
# récupère les probabilités prédites
nonparam_propensity_score<-
lapply(levels(factor(lalondedat$re74group)),
FUN=function(x){
cbind(lalondedat[re74group==x,
-c("re74group","treat")],
round(lm(paste0("treat ~",
specificationNP),
data=lalondedat[re74group==x])$fitted.values,
10))
})
nonparam_propensity_score<-unique(rbindlist(nonparam_propensity_score))
}
#Fonction qui permet de faire la comparaison entre toutes ces approches
# Il faut choisir une spécification pour les modèles paramétriques et une
# taille pour les pseudo-strates pour l'approche non-paramétrique
comparison_estimation_method<-function(specification,
taillepseudostrates){
paramdichtoresults<-sapply(c("logit",
"probit",
"cauchit"),
FUN=function(x){
estimationparamdichot(specification=
specification,
x)})
paramMCOresults<-estimationparamMCO(specification=specification)
lalondedat<-cbind(lalonde[,
c("re74")],
paramdichtoresults,
paramMCOresults)
colnames(lalondedat)[5]<-"MCO"
nonparamresults1<-estimationnonparam(taillepseudostrate = taillepseudostrates,
specificationNP = "1")
nonparamresults2<-estimationnonparam(taillepseudostrate = taillepseudostrates,
specificationNP = "re74")
lalondedat<-merge(lalondedat,
nonparamresults1,
by=c("re74"))
lalondedat<-merge(lalondedat,
nonparamresults2,
by=c("re74"))
colnames(lalondedat)[6]<-"Non-param. 1"
colnames(lalondedat)[7]<-"Non-param. 2"
lalondedat
}
specification_simple<-comparison_estimation_method(specification = "re74",
taillepseudostrates = 100)
cor(specification_simple[,-c("re74")])## logit probit cauchit MCO Non-param. 1 Non-param. 2
## logit 1.0000000 0.9987608 0.9681543 0.9721981 0.6596966 0.6563494
## probit 0.9987608 1.0000000 0.9558300 0.9819866 0.6442591 0.6413123
## cauchit 0.9681543 0.9558300 1.0000000 0.8971515 0.7448040 0.7371257
## MCO 0.9721981 0.9819866 0.8971515 1.0000000 0.5867835 0.5846558
## Non-param. 1 0.6596966 0.6442591 0.7448040 0.5867835 1.0000000 0.9952847
## Non-param. 2 0.6563494 0.6413123 0.7371257 0.5846558 0.9952847 1.0000000specification_souple<-comparison_estimation_method(specification = "re74 + u74",
taillepseudostrates = 100)
cor(specification_souple[,-c("re74")])## logit probit cauchit MCO Non-param. 1 Non-param. 2
## logit 1.0000000 1.0000000 0.9999994 0.9999996 0.9868464 0.9822143
## probit 1.0000000 1.0000000 0.9999993 0.9999998 0.9868535 0.9822219
## cauchit 0.9999994 0.9999993 1.0000000 0.9999983 0.9868023 0.9821655
## MCO 0.9999996 0.9999998 0.9999983 1.0000000 0.9868808 0.9822516
## Non-param. 1 0.9868464 0.9868535 0.9868023 0.9868808 1.0000000 0.9952847
## Non-param. 2 0.9822143 0.9822219 0.9821655 0.9822516 0.9952847 1.0000000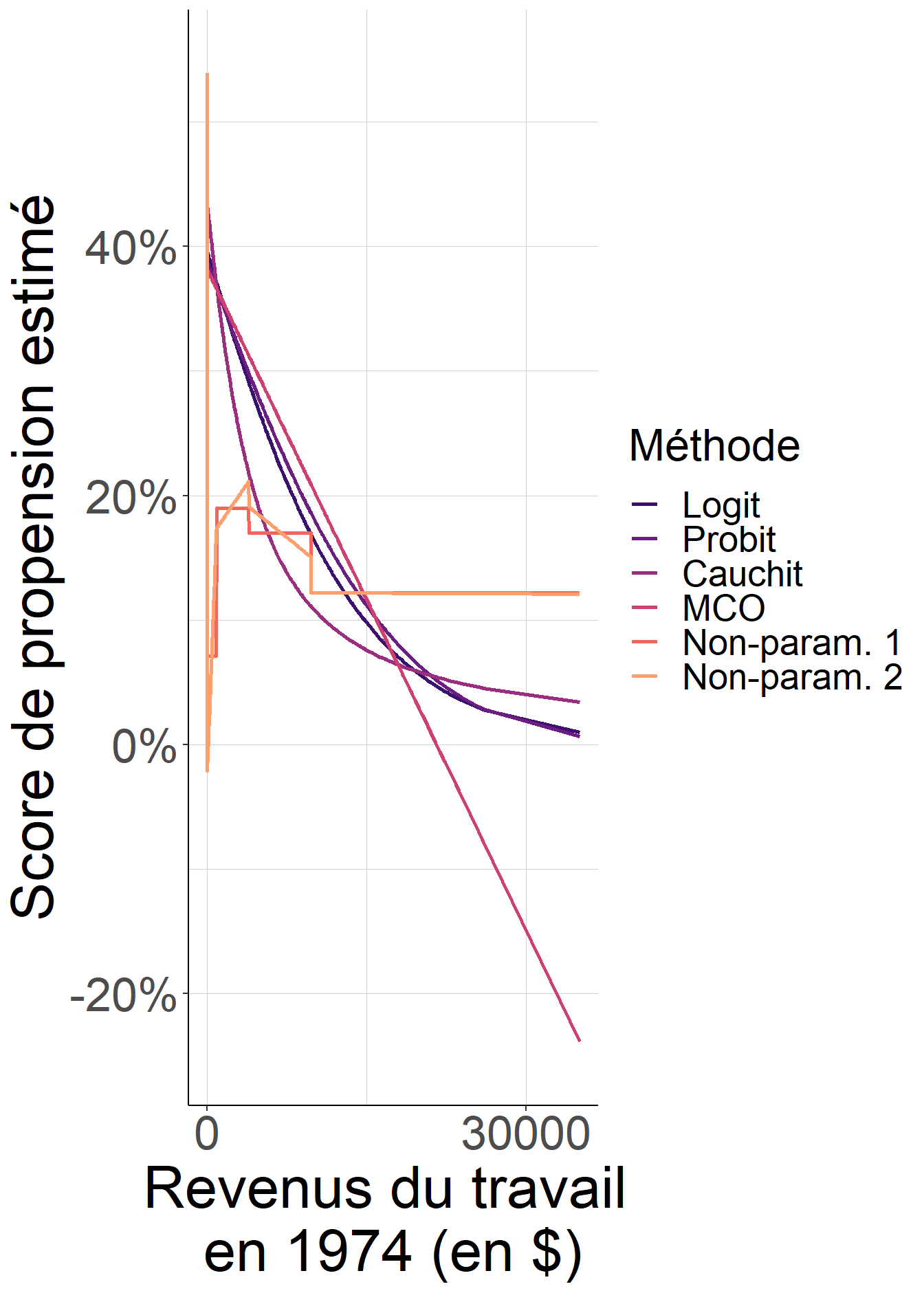
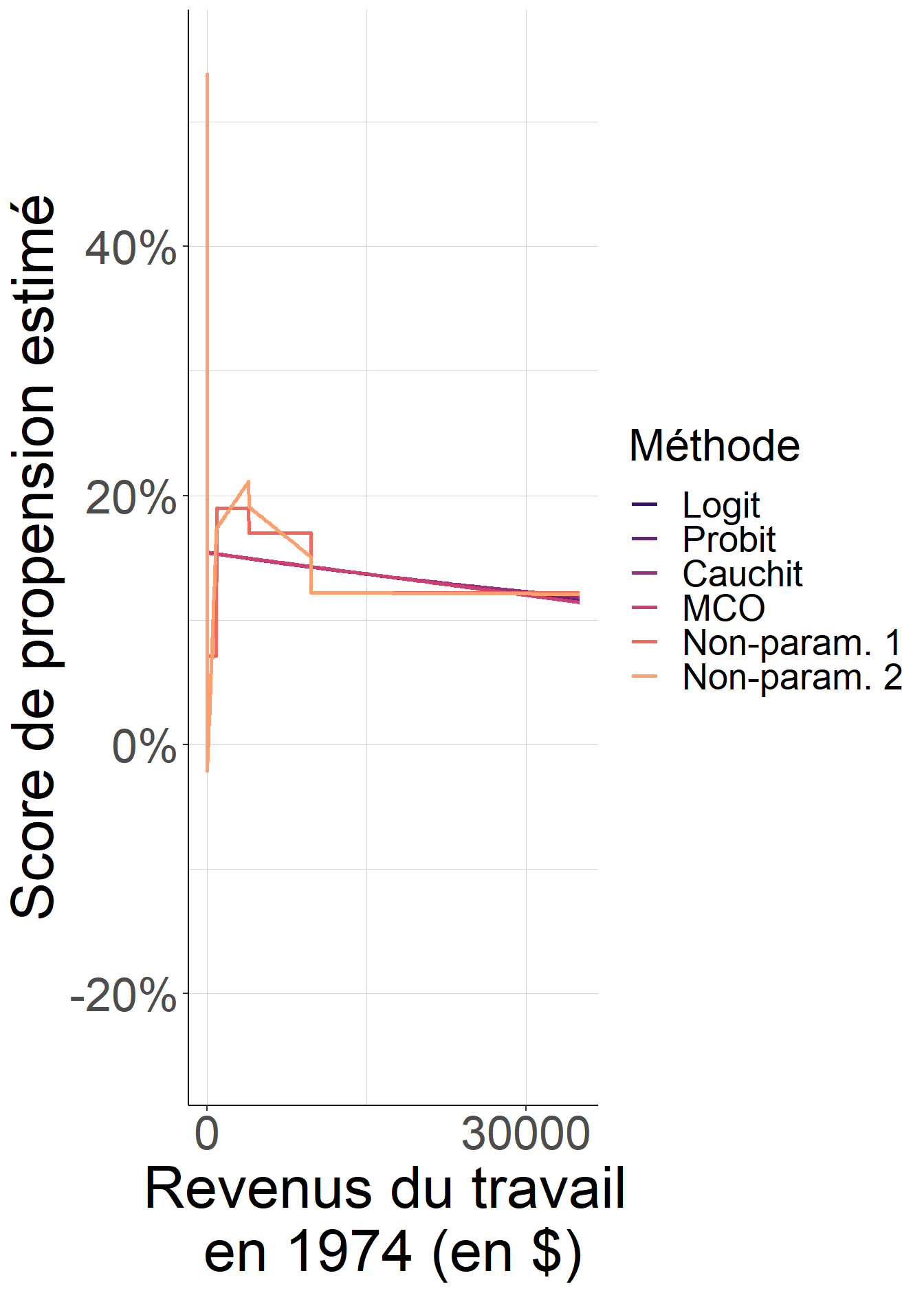
Figure 5.6: Lorsque l’on reste sur une spécification très simple, qui ignore la différence importante de comportement entre les individus dont les revenus du travail étaient nuls en 1974 et les autres, le choix de fonction de lien importe et peut conduire à des valeurs assez différentes du score de propension, et éventuellement assez éloignées de ce qu’une approche non-paramétrique flexible donnerait. En revanche, lorsque la spécification est plus flexible, ce choix de fonction de lien importe finalement assez peu.
5.5.3 Peut-on évaluer la qualité de l’estimation ?
L’estimation du score de propension demande de faire un certain nombre de choix – notamment choix de spécification et de fonction de lien – qu’il est souvent difficile de justifier a priori. Il est donc important de pouvoir évaluer la qualité de l’estimation découlant de ces choix : les paragraphes suivants proposent deux façon de procéder. Un point particulièrement important est que l’évaluation de cette qualité est faite sans utiliser à quelque moment que ce soit la variable d’intérêt \(Y_i\).
5.5.3.1 Vérifier la validité de l’hypothèse de support commun
Le passage par le score de propension a pour objet de pouvoir comparer à l’intérieur des plus grandes strates possibles les individus selon qu’ils ont fait ou non l’objet de l’intervention. Pour cela, il faut donc que pour chaque valeur possible \(p\) du score de propension, on dispose d’individus des deux groupes dont le score de propension est \(p\). En théorie, si l’on connaissait les vraies valeurs prises par le score de propension, il serait facile de tester l’hypothèse de support commun : si elle est vraie, alors on sait en effet que dans toutes les strates définies par les valeurs \(x\) prises par les variables de conditionnement, on doit pouvoir observer des individus des deux groupes, donc :
- le score de propension \(p(x):=\mathbb{P}(D_i=1 \mid X_i=x)\) est compris entre 0 et 1 strictement ;
- comme la petite strate définie par la valeur \(x\) des variables de conditionnement est incluse dans la grande strate définie par la valeur du score de propension \(p(x)\), on sait que l’on va forcément retrouver des individus des deux groupes dans la grande strate.
Inversement, si le score de propension est compris entre 0 et 1 strictement, alors pour toutes les valeurs possibles des variables de conditionnement on peut observer des individus des deux groupes. En effet, le score de propension est simplement la part du groupe qui fait l’objet de l’intervention dans chaque strate définie par une valeur prise par les variables de conditionnement.
Les choses deviennent plus compliquées lorsque l’on doit se contenter des valeurs estimées du score de propension au lieu de ses vraies valeurs ! En effet, tout l’enjeu de l’estimation tient à ce que même si l’on n’observe pas nécessairement pour chaque individu ayant fait l’objet de l’intervention un autre individu qui lui n’en a pas fait l’objet mais a exactement les mêmes valeurs des variables de conditionnement que le premier, on ne veut pas en déduire que son score de propension est égal à 1 comme on le ferait avec l’estimation naïve. On accepte donc une forme d’extrapolation.
Le danger est alors que notamment si l’on est trop rigide dans le choix de spécification, on impute à certains individus un score de propension compris entre 0 et 1 strictement même si l’hypothèse de support commun n’est pas respectée. Le fragment de code suivant explicte ce problème sur un jeu de données simulées.
library(data.table)
library(ggplot2)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
#avoir un exemple réplicable
set.seed(51651)
#On crée des données simulées pour lesquelles on connaît le vrai score de
# propension
#On commence par simuler une variable de conditionnement
simul_dat<-data.table(runif(100000,
min=0,
max=1))
colnames(simul_dat)<-c("x")
#On crée une variable qui stocke le vrai score de propension
#On génère une violation de l'hypothèse de support commun en mettant une
# région où celui-ci est nul
simul_dat[,
p:=fcase(
x<1/3,
0.3,
x<2/3,
0,
default=0.7
)]
#On génère la variable d'assignation à l'intervention à partir de ce
# vrai score de propension
simul_dat[,
d:=rbinom(size=1,
n=.N,
prob = p)]
#On estime le score de propension avec une spécification linéaire et une
# fonction de lien logistique
score_propension_estime<-glm(d ~ x,
data=simul_dat,
family=binomial(link=logit))$fitted.values
simul_dat<-cbind(simul_dat,
score_propension_estime)
#Visualisation
simul_dat_long<-melt(simul_dat[,
-c("d")],
id.vars = "x",
variable.name="score_propension",
value.name="valeur_pscore")
ggplot(data=simul_dat_long,
aes(x=x,
y=valeur_pscore,
group=score_propension,
linetype=score_propension))+
geom_line(color="red",
linewidth=1)+
scale_linetype(name="Score de propension",
labels=c("Réel",
"Estimé"))+
xlab("Variable de conditionnement")+
ylab("Score de propension")+
scale_y_continuous(labels=scales::percent)+
theme_classic()+
theme(text=element_text(size=16),#taille du texte
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),#grille de lecture
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))
Figure 5.7: Parce que l’on a fait un choix de spécification trop rigide, l’estimation paramétrique du score de propension conduit à imputer un score de propension compris entre 0 et 1 strictement (et même ici proche de 0.5) à un ensemble assez grand d’individus pour lesquels le vrai score de propension est nul. Le seul fait que les valeurs du score de propension estimée sont différente, et même assez éloignées de 0 et 1 ne suffit pas à repérer cette violation de l’hypothèse de support commun.
La situation n’est pas pour autant désespérée, et l’on peut tout de même utiliser le score de propension estimé pour repérer cette violation de l’hypothèse de support commun ! Pour cela, on peut repérer que sur la figure 5.7, il y a une grande plage de valeurs du score de propension estimé pour lesquelles le vrai score de propension est nul, c’est-à-dire pour lesquelles il n’y a en fait pas d’individu ayant fait l’objet de l’intervention. Le mieux est en fait de le repérer en étudiant la distribution du score de propension dans les groupes définis par le fait d’avoir fait ou non l’objet de l’intervention. Cela peut se faire par exemple en représentant un histogramme des valeurs du score de propension estimé pour chaque groupe défini par le statut vis-à-vis de l’intervention.
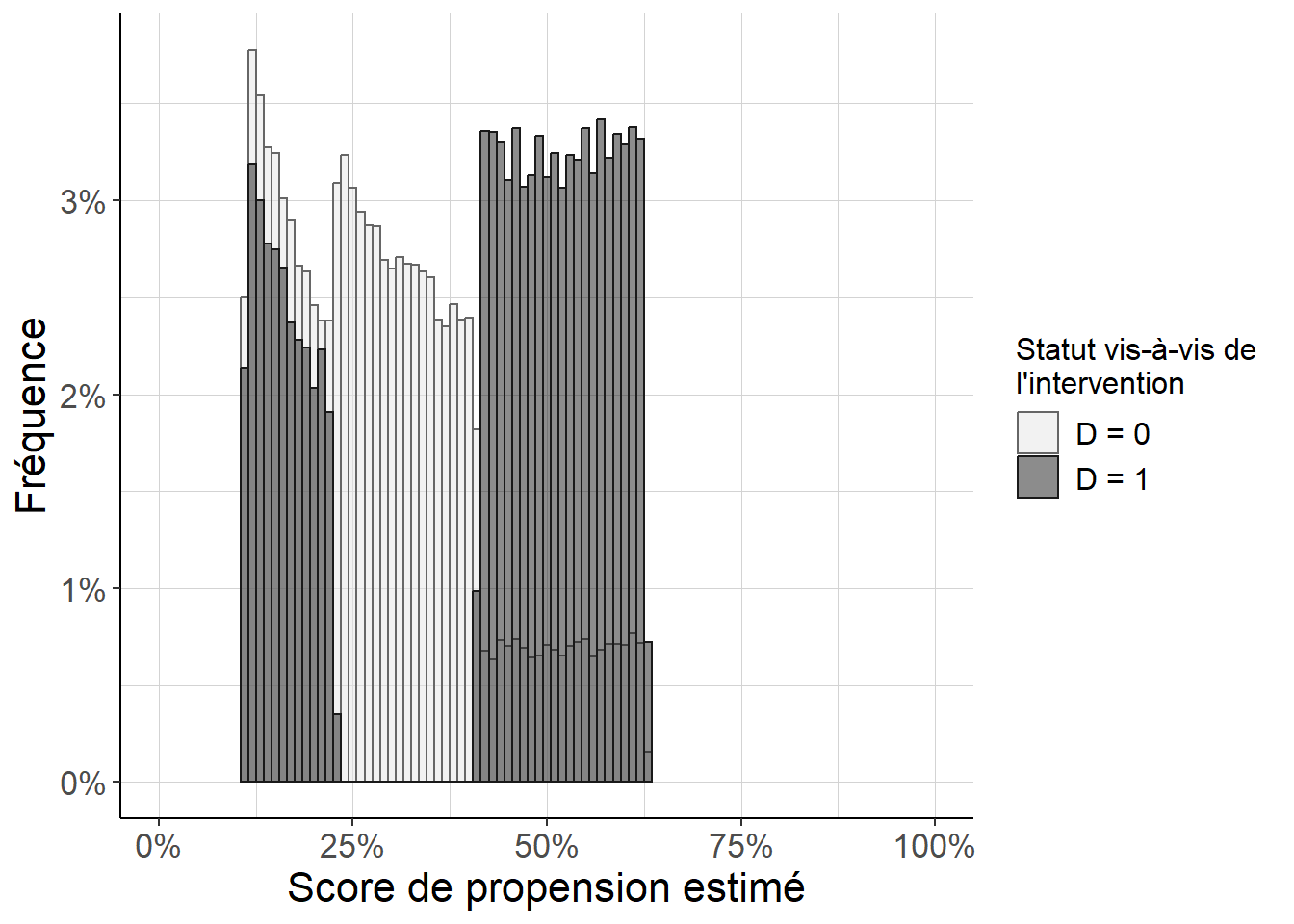
Figure 5.8: On repère ici que pour tout une plage de scores de propension estimée, il n’y a aucun individu ayant fait l’objet de l’intervention. Cela va poser un problème pour pouvoir faire la comparaison à l’interieur des strates définies par ces valeurs du score de propension estimée. De plus, comme les valeurs estimées du score de propension dans cette plage sont très éloignées de 0, qui est la vraie valeur du score de propension pour les strates au sein desquelles on ne peut pas faire la comparaison pertinente, cela signifie que la spécification retenue pour l’estimation du score de propension est inadaptée : les valeurs estimées du score de propension sont éloignées des vraies valeurs du score de propension.
5.5.3.2 Tester la propriété équilibrante du score de propension estimé
Si l’on connaissait les vraies valeurs prises par le score de propension, et non ses valeurs estimées, on saurait qu’en se plaçant à l’intérieur de strates définies par ces vraies valeurs, la distribution des caractéristiques observables définies par les variables de conditionnement est la même dans le groupe des individus qui ont fait l’objet de l’intervention et dans le groupe de ceux qui n’en ont pas fait l’objet. Pour vérifier que l’on dispose d’une estimation de qualité raisonnable du score de propension, une idée est donc de regarder si les valeurs estimées ont encore cette propriété, c’est-à-dire si, à l’intérieur de strates définies par les valeurs estimées du score de propension, la distribution des caractéristiques observables est bien la même dans les deux groupes.
Le fragment de code suivant se propose d’appliquer ces idées sur un exemple très proche de l’exemple précédent élaboré à partir de données simulées, mais cette fois-ci sans problème de support commun, en utilisant une technique de repondération.
library(data.table)
library(ggplot2)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
#avoir un exemple réplicable
set.seed(51651)
#On crée des données simulées pour lesquelles on connaît le vrai score de
# propension
#On commence par simuler une variable de conditionnement
simul_dat<-data.table(runif(100000,
min=0,
max=1))
colnames(simul_dat)<-c("x")
#On crée une variable qui stocke le vrai score de propension
#On génère une violation de l'hypothèse de support commun en mettant une
# région où celui-ci est nul
simul_dat[,
p:=fcase(
x<1/3,
0.3,
x<2/3,
0.01,
default=0.7
)]
#On génère la variable d'assignation à l'intervention à partir de ce
# vrai score de propension
simul_dat[,
d:=rbinom(size=1,
n=.N,
prob = p)]
#On estime le score de propension avec une spécification linéaire et une
# fonction de lien logistique
score_propension_estime<-glm(d ~ x,
data=simul_dat,
family=binomial(link=logit))$fitted.values
simul_dat<-cbind(simul_dat,
score_propension_estime)
#On génère les poids pertinents pour la repondération, en considérant aussi les
# poids normalement impossibles à utiliser que l'on construit directement à
# partir du vrai score de propension
simul_dat[,
c("poids",
"poids_infaisables"):=
list(d*(sum(d)/.N)/score_propension_estime+
(1-d)*(sum(1-d)/.N)/(1-score_propension_estime),
d*(sum(d)/.N)/p+
(1-d)*(sum(1-d)/.N)/(1-p))]
#On peut comparer l'écart relatif entre la valeur moyenne de la variable de
# conditionnement entre selon que l'on a ou pas fait l'objet de
# l'intervention, avec ou sans les poids
balancing_test<-simul_dat[,
list(diff_brute=(sum(d*x)/sum(d)-
sum((1-d)*x)/sum(1-d))/
(sum((1-d)*x)/sum(1-d)),
diff_repond=(sum(poids*d*x)/sum(poids*d)-
sum(poids*(1-d)*x)/sum(poids*(1-d)))/
(sum(poids*(1-d)*x)/sum(poids*(1-d))),
diff_repond_infaisables=
(sum(poids_infaisables*d*x)/
sum(poids_infaisables*d)-
sum(poids_infaisables*(1-d)*x)/
sum(poids_infaisables*(1-d)))/
(sum(poids_infaisables*(1-d)*x)/
sum(poids_infaisables*(1-d))))
]
balancing_test## diff_brute diff_repond diff_repond_infaisables
## 1: 0.4622634 -0.1127603 0.0007059366Dans cet exemple fictif, si la repondération à partir des valeurs estimées du score de propension permet de réduire l’écart relatif entre le groupe qui a fait l’objet de l’intervention et le groupe qui n’en ai pas fait l’objet, celui-ci reste relativement élevé (11.28% en valeur absolue), au contraire de ce qui serait le cas si on pouvait utiliser des poids estimés à partir du vrai score de propension (0.07%). Cela montre que ce test de la propriété équilibrante du score de propension estimé apporte une information intéressante sur la qualité et la pertinence du choix de spécification dans l’étape d’estimation.
On peut également refaire ce travail en comparant plusieurs approches possibles pour estimer le score de propension lorsque l’on reprend les données de Dehejia et Wahba (1999), en supposant toujours que conditionner sur les revenus du travail observés en 1974 suffit pour traiter l’entrée dans le NSW comme le résultat d’une expérience aléatoire contrôlée ou d’une expérience naturelle. On constate alors que lorsque l’on retient la spécification souple, l’écart relatif de revenu du travail en 1974 entre ceux qui sont entrés dans le programme et les autres, après l’étape de repondération, est très important, et dans certains cas plus prononcé (en valeur absolue) qu’il ne l’était avant repondération. Faire ce test aurait donc pu alerter sur les problèmes posés par cette spécification même sans passer par la comparaison avec l’approche non-paramétrique très flexible mais aussi assez coûteuse à introduire. Au contraire, lorsque l’on choisit la spécification souple, l’écart relatif est beaucoup plus faible, et tout à fait comparable à ce que l’on obtient dans l’approche non-paramétrique très souple. En somme, on dispose là d’un outil utile et assez discriminant pour mettre en évidence une situation problèmatique où le choix d’une spécification trop rigide peut conduire à des résultats erronés.
library(cobalt)
library(data.table)
library(ggplot2)
library(viridis)
#On récupère les données
data("lalonde")
lalonde<-data.table(lalonde)
#On crée la variable qui indique des revenus du travail nul en 1974
lalonde[,
u74:=as.numeric(re74==0)]
#Fonction qui renvoie les probabilités prédites d'entrée dans le programme
# pour chaque observation, pour un choix de spécification et une
# fonction de lien dans un modèle dichotomique
estimationparamdichot<-function(specification,
link_function){
glm(as.formula(paste0("treat ~",
specification)),
data = lalonde,
family = binomial(link = link_function))$fitted.values
}
#Fonction qui renvoie les probabilités prédites d'entrée dans le programme
# pour chaque observation, pour un choix de spécification et une estimation
# par les moindres carrés ordinaires
estimationparamMCO<-function(specification){
lm(as.formula(paste0("treat ~",
specification)),
data=lalonde)$fitted.values
}
#Tentative d'estimation non-paramétrique : on regroupe les observations par
# pseudostrates de taille minimale définie (en nombre d'observations) et on
# calcule la part des individus entrés dans le programme à l'intérieur de
# chacune de ces strates
estimationnonparam<-function(taillepseudostrate,
specificationNP){
#On récupère le nombre d'individus observés pour chaque niveau de revenu
re74groups_lalonde<-setorder(lalonde[,
list(nb_indiv=.N),
by=c("re74")],
re74)
#On associe à chaque niveau de revenu une pseudostrate en première intention
# en faisant des groupes de taille au moins pseudokernel en partant de 0
re74groups_lalonde[,
nb_cumul_indiv:=cumsum(nb_indiv)]
re74groups_lalonde[,
re74group:=floor(nb_cumul_indiv/
taillepseudostrate)*
taillepseudostrate]
#Il faut faire attention car la dernière pseudostrate est potentiellement
# toute petite ! On la réagrège avec l'avant dernière
derniergroupe=max(re74groups_lalonde$re74group)
if(max(re74groups_lalonde[re74group==derniergroupe]$nb_cumul_indiv-
derniergroupe)<=taillepseudostrate)
{
avantderniergroupe<-
max(re74groups_lalonde[re74group!=derniergroupe]$re74group)
re74groups_lalonde[re74group==derniergroupe,
re74group:=avantderniergroupe]
}
#Il faut aussi mettre le groupe des 0 à part
re74groups_lalonde[re74==0,
re74group:=0]
#On peut remettre chaque individu dans son groupe
lalondedat<-merge(lalonde[,
c("re74",
"treat")],
re74groups_lalonde[,
c("re74",
"re74group")],
by=c("re74"))
#Dans chaque groupe on estime un modèle de probabilité linéaire et on
# récupère les probabilités prédites
nonparam_propensity_score<-
lapply(levels(factor(lalondedat$re74group)),
FUN=function(x){
cbind(lalondedat[re74group==x,
-c("re74group","treat")],
round(lm(paste0("treat ~",
specificationNP),
data=lalondedat[re74group==x])$fitted.values,
10))
})
nonparam_propensity_score<-unique(rbindlist(nonparam_propensity_score))
}
#Fonction qui permet de faire la comparaison entre toutes ces approches
# Il faut choisir une spécification pour les modèles paramétriques et une
# taille pour les pseudo-strates pour l'approche non-paramétrique
comparison_estimation_method<-function(specification,
taillepseudostrates){
paramdichtoresults<-sapply(c("logit",
"probit",
"cauchit"),
FUN=function(x){
estimationparamdichot(specification=
specification,
x)})
paramMCOresults<-estimationparamMCO(specification=specification)
lalondedat<-cbind(lalonde[,
c("re74",
"treat")],
paramdichtoresults,
paramMCOresults)
colnames(lalondedat)[6]<-"MCO"
nonparamresults1<-estimationnonparam(taillepseudostrate = taillepseudostrates,
specificationNP = "1")
nonparamresults2<-estimationnonparam(taillepseudostrate = taillepseudostrates,
specificationNP = "re74")
lalondedat<-merge(lalondedat,
nonparamresults1,
by=c("re74"))
lalondedat<-merge(lalondedat,
nonparamresults2,
by=c("re74"))
colnames(lalondedat)[7]<-"Non-param. 1"
colnames(lalondedat)[8]<-"Non-param. 2"
lalondedat
}
specification_simple<-comparison_estimation_method(specification = "re74",
taillepseudostrates = 100)
specification_souple<-comparison_estimation_method(specification = "re74 + u74",
taillepseudostrates = 100)
#On calcule les poids associés à chaque estimation du score de
# propension et on fait le test de la propriété équilibrante
specification_simple[,indiv_id:=as.character(.I)]
#On met tout dans une table
estimations<-rbind(specification_simple[,indiv_id:=as.character(.I)],
specification_souple[,indiv_id:=as.character(.I)],
idcol="specification")
#Plus facile à manipuler en format long
estimations<-melt(estimations,
id.vars=c("specification",
"indiv_id",
"re74",
"treat"),
variable.name=c("link_function"),
value.name="pscore")
#On met aussi l'écart brut
estimations<-rbind(estimations,
estimations[link_function=="logit"][
,
c("link_function",
"pscore"):=list("ecart_brut",
sum(lalonde$treat)/nrow(lalonde))])
#On crée le jeu de poids pour chaque estimation du score de propension
estimations[,
poids:=treat*(sum(treat)/.N)*(1/pscore)+
(1-treat)*(sum(1-treat)/.N)*(1/(1-pscore)),
by=list(specification,
link_function)]
balancing_test<-estimations[,
list(balancing_test=
(sum(treat*poids*re74)/
sum(treat*poids)-
sum((1-treat)*poids*re74)/
(sum((1-treat)*poids)))/
(sum((1-treat)*poids*re74)/
sum((1-treat)*poids))),
by=c("specification",
"link_function")]
Figure 5.9: En s’intéressant à la différence repondérée du revenu du travail moyen en 1974 entre les individus participant au NSW et les autres, on voit que lorsque l’on choisit la spécification simple, cet écart est très grand, et même parfois pire que celui que l’on observe sans repondération. Au contraire, le choix d’une spécification à peine plus souple, qui permet simplement la distinction entre ceux qui n’ont perçu aucun revenu du travail en 1974 et les autres conduit à des poids qui rendent beaucoup plus comparables les deux groupes. Ainsi, tester la propriété équilibrante du score de propension, ici par repondération, permet de mettre à l’épreuve l’adéquation du choix de spécification au problème étudié, et le cas échéant de rejeter les spécifications inadaptées.
Remarque
On a ici proposé de considérer l’écart relatif entre le groupe des individus entrés dans le programme et celui de ceux qui n’y sont pas entrés pour tester la propriété équilibrante du score de propension estimé. Cela ne pose pas de problème dans la mesure où, dans cet exemple, on ne considère qu’une seule variable de conditionnement, les revenus du travail observés en 1974. Lorsque l’on considère plusieurs variables, il est fréquent de considérer la différence des moyennes pour chaque variable, divisée par (un terme proportionnel à) l’écart-type de cette variable, c’est-à-dire à la racine carrée de sa variance. L’intéret est que cela permet de faire des comparaisons entre variables de conditionnement sans avoir à se soucier de leurs niveaux moyens ou de l’échelle avec laquelle elles sont mesurées. Il est important lorsque l’on fait cela de s’assurer que l’on utilise bien le même écart-type au dénominateur avant et après l’étape de stratification, d’appariement ou de repondération : seule l’écart moyen au numérateur doit changer (Stuart (2010))
Une voie alternative est celle de l’estimation non-paramétrique, par exemple en ayant recours à ce que l’on appelle un estimateur à noyau, qui exploite bien un concept de proximité entre observations, mais sans aller jusqu’à supposer une structure aussi contraignant sur la dépendance entre score de propension et variables de conditionnement.↩︎