1.3 Variables aléatoires réelles unidimensionnelles
Cette sous-section vise à récapituler certains concepts dans le cas des variables aléatoires réelles unidimensionnelles. La sous-section suivante généralise ensuite ces concepts au cas multidimensionnel. C’est en général le cas multidimensionnel qui est utile pour une bonne compréhension des concepts liés aux régressions linéaires. Cela étant, l’intuition acquise sur le cas uniidimensionnel se généralise sans difficulté particulière au cas multidimensionnel. Ce chapitre fait en conséquence le choix de détailler le cas unidimensionnel, en particulier en ce qui concerne les concepts d’espérance (1.3.2) et d’espérance conditionnelle (1.3.3), ainsi que leurs liens avec la moyenne empirique (1.3.6), avant de passer au cas général (1.4).
1.3.1 Loi, distribution et quantiles
Définition
La loi de probabilité d’une variable aléatoire réelle est la fonction qui à chaque sous-ensemble de la droite réelle associe la probabilité, comprise entre 0 et 1, que les valeurs de cette variable aléatoire appartiennent à ce sous-ensemble. On parle aussi parfois de distribution de cette variable aléatoire.
Avertissement
La loi de probabilité d’une variable aléatoire ne suffit pas à la caractériser.
Pour s’en convaincre, on peut considérer l’expérience aléatoire consistant à tirer aléatoirement et de façon uniforme un individu dans la population française. Si \(X\) désigne la variable aléatoire qui renvoie 1 lorsque l’âge de l’individu tiré est inférieur à l’âge médian, et 0 sinon, et \(Y\) désigne la variable aléatoire qui renvoie 1 lorsque la taille de l’individu tiré est inférieure à la taille médiane, alors \(X\) et \(Y\) ont la même loi, mais \(X\) et \(Y\) ne coïncident par (il existe des individus \(\omega\) qui sont à la fois âgés (\(X(\omega)\)=0) et de grande taille (\(Y(\omega)=1\))).
Définition
À toute variable aléatoire réelle peut être associée une fonction de la droite réelle \(\mathbb{R}\) vers le segment \([0,\, 1]\) appelée fonction de répartition. La fonction de répartition de la variable aléatoire \(X\) associe à chaque nombre réel \(x\) la probabilité que \(X\) prenne des valeurs inférieures ou égales \(x\), c’est-à-dire \(\mathbb{P}(X \leq x)\).
La fonction de répartition d’une variable aléatoire réelle permet de définir sa fonction quantile.
Définition
En notant \(F\) la fonction de répartition de la variable aléatoire réelle \(X\), la fonction quantile de \(X\) est une fonction \(G\) du segment \([0,\, 1]\) dans la droite réelle achevée \(\bar{\mathbb{R}}\), c’est-à-dire l’union de la droite réelle \(\mathbb{R}\) et de l’ensemble contenant les deux infinis \(\left\{-\infty,\, +\infty\right\}\). À tout \(q\) compris entre 0 et 1, la fonction quantile \(G\) associe le plus grand nombre \(G(q)\) (y compris les deux infinis) tel que pour tout \(x\), si \(F(x)\) est supérieur ou égal à \(q\), alors \(x\) est supérieur ou égal à \(G(q)\).
Par exemple, si \(X\) désigne la taille en cm dans la population française, alors la taille médiane \(G(\frac{1}{2})\) est la taille telle que pour toute autre taille \(x\), si au moins 50% de la population française est d’une taille inférieure ou égale à \(x\), alors \(x\) est supérieure ou égale à \(G(\frac{1}{2})\).
À retenir
La fonction de répartition et la fonction quantile caractérisent de façon unique la loi de probabilité d’une variable aléatoire réelle. En d’autres termes, deux variables aléatoires réelles ont la même loi de probabilité si et seulement si elles ont la même fonction de répartition, ou de façon équivalente si et seulement si elles ont la même fonction quantile.
1.3.2 Espérance
Définition
L’espérance d’une variable aléatoire correspond à la moyenne des valeurs possibles de cette variable aléatoire, avec des poids égaux à la probabilité de réalisation de chacune de ces valeurs.
Lorsque la variable aléatoire réelle \(X\) prend un nombre fini \(n\) de valeurs, que l’on peut noter \(x_1\) à \(x_n\), son espérance, notée \(\mathbb{E}[X]\) est la somme de ces valeurs, pondérées par leur probabilité de réalisation :
\[\mathbb{E}[X] := \sum_{i=1}^n x_i \mathbb{P}(X=x_i)\]
Par exemple, si l’expérience consiste en le lancer d’un dés à six faces, et que la variable aléatoire considérée est le résultat de ce lancer, alors l’espérance est, dans le cas où le dé est bien équilibré \(\frac{1+2+3+4+5+6}{6}=3.5\).
De même, si l’expérience aléatoire consiste en le tirage aléatoire équiprobable d’un individu dans la population des salariés français, et que la variable aléatoire considérée est le salaire de cet individu, alors l’espérance de cette variable aléatoire est \(\frac{1}{N}\sum_{i \in \mathcal{I}} w_i\), où \(N\) est le nombre de salariés français, et \(w_i\) désigne le salaire du salarié \(i\). En d’autres termes, l’espérance est le salaire moyen dans toute la population, par opposition au salaire moyen dans l’échantillon observé, ici de taille 1.
Si on considère l’expérience aléatoire consistant à tirer aléatoirement de façon équiprobable un individu dans la population des actifs français, et que l’on considère la variable aléatoire qui vaut 1 si cet individu est au chômage, et 0 sinon, alors l’espérance de cette variable aléatoire est égale au taux de chômage, c’est-à-dire à la proportion de chômeurs dans la population active.
De façon plus générale, si \(X\) est une variable aléatoire dichotomique, c’est-à-dire une variable aléatoire dont les valeurs appartiennent à l’ensemble \(\{0,\, 1 \}\), alors \(\mathbb{E}[X]=\mathbb{P}(X=1)\).
Cette définition peut être généralisée à un ensemble beaucoup plus vaste de variables aléatoires – les variables aléatoires intégrables – dans un cadre fondé sur l’intégrale de Lebesgue. Dans tout le reste de ce texte, on supposera toujours que toutes les variables sont intégrables, c’est-à-dire que toutes les espérances sont bien définies, et de valeur finie.
L’espérance possède les propriétés essentielles suivantes.
À retenir
Monotonie : si \(X\) et \(Y\) sont deux variables aléatoires réelles portant sur la même expérience telles que pour tout résultat possible de l’expérience \(\omega\) on ait \(X(\omega) \leq Y(\omega)\), alors \(\mathbb{E}[X] \leq \mathbb{E}[Y]\).
À retenir
Linéarité : si \(X\) et \(Y\) sont deux variables aléatoires réelles portant sur la même expérience, et si \(\lambda\) et \(\mu\) sont deux nombres réels, alors \(\mathbb{E}[\lambda X + \mu Y] = \lambda \mathbb{E}[X] + \mu \mathbb{E}[Y]\).
Deux variables aléatoires \(X\) et \(Y\) de même loi ont la même espérance. La réciproque n’est en revanche pas vraie. Ainsi, si \(X\) est la variable aléatoire constante égale à 0, et \(Y\) une variable aléatoire qui vaut -1 avec la probabilité \(\frac{1}{2}\) et 1 avec la probabilité \(\frac{1}{2}\), alors \(\mathbb{E}[X]=\mathbb{E}[Y]\), mais \(X\) et \(Y\) n’ont pas la même loi.
Avertissement
Il importe de distinguer le concept d’espérance d’une variable aléatoire du concept de moyenne empirique. En effet, l’espérance est un nombre réel qui n’est pas soumis à des variations aléatoires, tandis que la moyenne empirique est une grandeur qui dépend du tirage aléatoire d’un échantillon et doit donc être considérée comme une variable aléatoire.
1.3.3 Espérance conditionnelle
Définition
Si \(X\) et \(Y\) sont deux variables aléatoires portant sur la même expérience aléatoire, alors l’espérance conditionnelle \(\mathbb{E}[Y\mid X]\) est une variable aléatoire portant sur cette expérience aléatoire. Plus précisément, pour un résultat possible \(\omega\), l’espérance conditionnelle \(\mathbb{E}[Y\mid X] (\omega)\) correspond à la moyenne des valeurs possibles de \(Y\) avec des poids égaux à la probabilité de réalisation de chacune de ces valeurs à l’intérieur de l’ensemble des résultats possibles \(\omega'\) tels que \(X(\omega')=X(\omega)\).
Cette définition implique que si \(\omega\) et \(\omega'\) vérifient \(X(\omega)=X(\omega')\), alors \(\mathbb{E}[Y\mid X](\omega)=\mathbb{E}[Y\mid X](\omega')\). Par conséquent, l’espérance conditionnelle \(\mathbb{E}[Y\mid X]\) ne peut pas varier de façon plus fine que \(X\), au contraire de \(Y\) : en général, on peut très bien avoir \(Y(\omega) \neq Y(\omega')\) quand bien même \(X(\omega)=X(\omega')\).
Par exemple, si l’expérience considérée est le tirage équiprobable d’un salarié dans la population des salariés français, que \(X\) est la variable aléatoire qui renvoie le sexe à l’état-civil de ce salarié, et \(Y\) la variable aléatoire qui renvoie son salaire, alors \(\mathbb{E}[Y \mid X]\) est la variable aléatoire qui renvoie le salaire moyen des femmes dans toute la population si l’individu tiré est une femme, et le salaire moyen des hommes dans toute la population si l’individu tiré est un homme.
Si \(X\) et \(Y\) sont deux variables aléatoires prennent un nombre fini de valeurs notées \(x_1\) à \(x_m\) et \(y_1\) à \(y_n\), alors l’espérance conditionnelle de \(Y\) sachant \(X\), notée \(\mathbb{E}[Y \mid X]\) est la variable aléatoire définie par : \[\mathbb{E}[Y \mid X] := \sum_{i=1}^m \mathbf{1}_{\{x_i\}}(X) \frac{\sum_{j=1}^n y_j \mathbb{P}(X=x_i, Y=y_j)}{\sum_{j=1}^n \mathbb{P}(X=x_i, Y=y_j)}\] où \(\mathbf{1}_{\{x_i\}}(X)\) est la variable aléatoire qui vaut 1 si \(X=x_i\) et 0 sinon. En d’autres termes, \(\mathbb{E}[Y \mid X]\) correspond à la somme des valeurs possibles de \(Y\) pondérées par leur probabilité de réalisation étant donnée la valeur de \(X\). Il importe de noter que dans ce cas des variables aléatoires prenant un nombre fini de valeurs, l’espérance conditionnelle \(\mathbb{E}[Y \mid X]\) a au plus le même nombre \(m\) de valeurs que \(X\) (qui diffère en général du nombre de valeurs possibles \(n\) de \(Y\)).
En choisissant un certain \(x_i\) fixé, il est également possible de considérer l’espérance conditionnelle de \(Y\) sachant \(X=x_i\) comme un nombre réel et non plus une variable aléatoire. Celui-ci est tout simplement défini par : \[\mathbb{E}[Y \mid X=x_i] := \frac{\sum_{j=1}^n y_j \mathbb{P}(X=x_i, Y=y_j)}{\sum_{j=1}^n \mathbb{P}(X=x_i, Y=y_j)}\] Ces définitions peuvent être étendues plus généralement aux variables aléatoires intégrables, et non aux seules variables aléatoires ne prenant qu’un nombre fini de valeurs.
À retenir
Les propriétés fondamentales de l’espérance – monotonie et linéarité – valent également pour l’espérance conditionnelle.
L’espérance conditionnelle a de surcroît plusieurs propriétés qui en font un outil particulièrement important dans la panoplie de la statisticienne et du statisticien.
À retenir
Si \(\phi\) est une fonction quelconque, alors \(\mathbb{E}[\phi(X) Y \mid X] = \phi(X) \mathbb{E}[Y \mid X]\).
Une conséquence immédiate de cette propriété est qu’en prenant pour \(Y\) la variable aléatoire constante égale à 1, et en raisonnant pour un certain \(x\) fixé : \(\mathbb{E}[\phi(X) \mid X=x] = \phi(x)\).
À retenir
Une autre propriété essentielle de l’espérance conditionnelle est la loi des espérances itérées : l’espérance de l’espérance conditionnelle est égale à l’espérance.
si \(X\) et \(Y\) sont deux variables aléatoires réelles, alors \(\mathbb{E}[Y] = \mathbb{E}\left[\mathbb{E}\left[ Y \, | \, X\right]\right]\). Dans le cas où \(X\) prend un nombre fini \(m\) de valeurs \(x_1\) à \(x_m\), cette égalité peut également s’écrire sous la forme d’une somme pondérée : \[\mathbb{E}[Y] = \sum_{i=1}^m \mathbb{E}[Y \mid X=x_i] \mathbb{P}(X=x_i)\] En d’autres termes, l’espérance de \(Y\) est la moyenne des espérances conditionnelles de \(Y\) sachant que \(X\) prend chaque valeur possible, avec un poid égal à la probabilité que \(X\) prenne effectivement cette valeur.
On peut pour comprendre ce résultat revenir à l’exemple du tirage équiprobable d’un salarié dans la population des salariés français, où \(X\) est la variable aléatoire qui renvoie le sexe à l’état-civil de ce salarié, et \(Y\) la variable aléatoire qui renvoie son salaire. Dans ce cas, l’espérance conditionnelle \(\mathbb{E}[Y \mid X] (\omega)\) est égale au salaire moyen des femmes si \(\omega\) est une femme, et au salaire moyen des hommes si \(\omega\) est un homme. Par ailleurs, l’espérance \(\mathbb{E}[Y]\) est le salaire moyen dans toute la population. La loi des espérances itérées affirme simplement que dans cette espérance est égale à la moyenne des espérances conditionnelles, avec des poids égaux à la probabilité que l’on ait tiré ou bien une femme ou bien un homme. Comme ces probabilités sont égales à la part de femmes et d’hommes dans la population totale, cela revient à dire que le salaire moyen sur toute la population des salariés n’est autre que la moyenne du salaire moyen des femmes et du salaire moyen des hommes, avec des poids égaux aux parts respectives des deux sexes.
À retenir
Si deux variables aléatoires réelles \(X\) et \(Y\) sont indépendantes, alors l’espérance conditionnelle \(\mathbb{E}[Y \mid X]\) est constante.
En d’autres termes, si \(X\) et \(Y\) sont indépendantes, alors \(\mathbb{E}[Y \mid X] = \mathbb{E}[Y]\). La réciproque n’est en revanche pas vraie. En effet, si \(Z\) est une variable aléatoire qui vaut -1 avec la probabilité \(\frac{1}{2}\) et 1 avec la probabilité \(\frac{1}{2}\), et \(X\) une variable aléatoire indépendante de \(Z\) et suivant une loi uniforme sur le segment \([0,\,1]\), alors \(\mathbb{E}[ZX \mid X] = 0\), mais \(X\) et \(ZX\) ne sont pas indépendantes.
Le fragment de code suivant permet de visualiser le nuage de points généré par le tirage indépendant de 1000 couples de variables aléatoires \((X_i, Y_i)\) de même loi jointe, tels que \(\mathbb{E}[Y_i \mid X_i]= \mathbb{E}[Y_i]\) mais \(Y_i\) et \(X_i\) ne sont pas indépendantes.
library(data.table)
library(ggplot2)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
# avoir un exemple réplicable
set.seed(651351)
#On fixe le nombre de tirages
nbr_tirages<-1000
#On tire nbr_tirages valeurs de X indépendamment avec une loi uniforme sur [0, 1]
x_valeurs<-runif(nbr_tirages,
min=0,
max=1)
#On tire nbr_tirages valeurs de Z indépendamment avec une loi uniforme sur [-1, 1]
z_valeurs<-runif(nbr_tirages,
min=-1,
max=1)
#On réunit les valeurs dans un data.table
table_valeurs<-data.table(x_valeurs,
z_valeurs)
#On crée les variables Y:=ZX
table_valeurs[,
y_valeurs:=x_valeurs*z_valeurs]
#On crée une figure agréable à l'aide du package ggplot2
ggplot(data=table_valeurs,
aes(x=x_valeurs,
y=y_valeurs))+
geom_point(color="gray")+#visualiser sour la forme d'un nuage de points
xlab("Valeur de X")+#Nom des axes
ylab("Valeur de Y")+
geom_hline(yintercept=0,
color="red")+#une ligne rouge pour l'espérance conditionnelle
annotate("text",
x=0.75,
y=-0.125,
label="Espérance conditionnelle : 0",
size=4,
color="red")+#Donner un label à la ligne rouge
theme_classic()+#enlever l'arrière-plan gris par défaut
theme(text=element_text(size=16),
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))#le quadrillage léger![La variable aléatoire \(Y\) n’est pas indépendante de \(X\) : sa dispersion n’est pas la même selon la valeur de \(X\). En revanche, son espérance conditionnelle \(\mathbb{E}[Y \mid X]\) est constante et égale à 0 : \(Y\) est indépendante en moyenne de \(X\).](main_files/figure-html/mean-independence-1.png)
Figure 1.1: La variable aléatoire \(Y\) n’est pas indépendante de \(X\) : sa dispersion n’est pas la même selon la valeur de \(X\). En revanche, son espérance conditionnelle \(\mathbb{E}[Y \mid X]\) est constante et égale à 0 : \(Y\) est indépendante en moyenne de \(X\).
Ces considérations permettent de proposer un concept distinct de l’indépendance.
Définition
Si \(X\) et \(Y\) sont deux variables aléatoires réelles, \(Y\) est indépendante en moyenne de \(X\) si l’espérance conditionnelle \(\mathbb{E}[Y \mid X]\) est indépendante de \(X\).
Formellement, cette définition équivaut à \(\mathbb{E}[Y \mid X] = \mathbb{E}[Y]\). Le paragraphe précédent montre que si \(X\) et \(Y\) sont indépendantes, alors \(Y\) est indépendante en moyenne de \(X\), mais que la réciproque n’est pas vraie : dans le contre-exemple proposé, \(Y=ZX\) est indépendante en moyenne de \(X\) mais \(X\) et \(Y\) ne sont pas indépendantes.
Par ailleurs, \(Y\) peut être indépendante en moyenne de \(X\) sans que \(X\) soit indépendante en moyenne de \(Y\), alors que le concept d’indépendance est symétrique. Ainsi, dans le contre-exemple examiné, \(Y=ZX\) est indépendante en moyenne de \(X\), mais \(X\) n’est pas indépendante en moyenne de \(Y\). En effet, \(\mathbb{E}[X \mid Y] = |Y|\) varie bien avec \(Y\).
Si \(e\) est un événement, c’est-à-dire un sous-ensemble de l’ensemble des cas possibles, alors on peut lui associer la variable aléatoire \(X_e\) qui vaut 1 si \(e\) se produit et 0 sinon.
Définition
Si \(A\) et \(B\) sont deux événements, alors on peut définir la probabilité conditionnelle de \(A\) sachant \(B\) comme l’espérance conditionnelle \(\mathbb{P}(A \mid B):=\mathbb{E}[X_A \mid X_B=1]\).
En reprenant la définition formelle de l’espérance conditionnelle, cette définition se ramène à : \[\mathbb{P}(A \mid B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}\]
On dispose enfin de la formule de Bayes qui permet de passer du conditionnement d’un événement par un autre au conditionnement inverse :
À retenir
Si \(A\) et \(B\) sont deux événements, alors \(\mathbb{P}(A \mid B) = \frac{\mathbb{P}(A)}{\mathbb{P}(B)}\mathbb{P}(B \mid A)\)
1.3.4 Variance et écart-type
Définition
Si \(X\) est une variable aléatoire réelle intégrable, alors sa variance, notée \(\mathcal{V}(X)\) est définie comme l’espérance du carré de l’écart de \(X\) à son espérance.
Formellement, cette définition s’écrit simplement : \(\mathcal{V}(X) := \mathbb{E}\left[\left(X - \mathbb{E}\left[X\right]\right)^2\right]\). Une définition équivalente est \(\mathcal{V}(X) := \mathbb{E}\left[X^2\right] - \mathbb{E}\left[X\right]^2\). Un calcul qui mobilise les propriétés élémentaires de l’espérance permet d’établir l’équivalence des deux définitions.
Définition
L’écart-type de la variable aléatoire réelle \(X\), que l’on peut noter \(\sigma(X)\) est défini comme la racine carrée de sa variance.
Autrement dit, cette définition s’écrit simplement : \(\sigma(X) := \sqrt{\mathcal{V}(X)}\).
En revenant à l’exemple du tirage équiprobable d’un individu dans la population active, et à la variable indicatrice qui vaut 1 si cet individu est au chômage et 0 sinon, on se souvient que l’espérance de cette variable aléatoire est égale au taux de chômage, que l’on peut noter \(\tau\). Comme les valeurs de cette variable aléatoire sont 0 et 1, on peut voir que cette variable aléatoire est égale à son carré. En effet, pour tout tirage possible d’un individu \(\omega\) : ou bien \(\omega\) est chômeur, et dans ce cas \(X(\omega)^2 = 1 =X(\omega)\), ou bien il n’est pas chômeur et dans ce cas \(X(\omega)^2=0 = X(\omega)\). Par conséquent, la variance de cette variable aléatoire est égale à \(\tau - \tau^2 = \tau (1-\tau)\), et son écart-type à \(\sqrt{\tau(1-\tau)}\).
Ce résultat se généralise à toutes les variables aléatoires dichotomiques, c’est-à-dire à toutes les variables aléatoires dont les valeurs appartiennent à l’ensemble \(\{0, \, 1\}\). Pour celles-ci, on a toujours \(\mathcal{V}(X)=\mathbb{E}[X]\{1-\mathbb{E}[X]\}\).
À retenir
La variance \(\mathcal{V}(X)\) quantifie en un sens la dispersion de la variable aléatoire \(X\).
En effet, la variable aléatoire \(X\) est constante si et seulement si elle est de variance nulle. On dispose de plus de l’inégalité de Bienaymé-Tchebychev : si \(\alpha\) est un nombre réel strictement positif, alors \(\mathbb{P}(|X-\mathbb{E}[X]|\geq \alpha) \leq \frac{\mathcal{V}(X)}{\alpha^2}\). Ainsi, plus la variance d’une variable aléatoire est faible, plus il est improbable qu’elle prenne des valeurs éloignées de son espérance.
1.3.5 Covariance et corrélation
Définition
Si \(X\) et \(Y\) sont deux variables aléatoires réelles définie sur le même espace de départ, alors leur covariance est définie comme la différence entre l’espérance de leur produit et le produit de leurs espérances.
Formellement, cette définition s’écrit : \(\mathcal{C}(X, Y) := \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y]\). Une définition équivalente est \(\mathcal{C}(X, Y) := \mathbb{E}\left[\left(X-\mathbb{E}[X]\right)\left(Y-\mathbb{E}[Y]\right)\right]\). L’équivalence des deux définitions peut se montrer en revenant aux propriétés élémentaires de linéarité de l’espérance.
La covariance a les propriétés fondamentales suivantes.
À retenir
Bilinéarité : si \(X\), \(Y\) et \(Z\) sont trois variables aléatoires réelles définies sur la même expérience aléatoire, et si \(\lambda\) et \(\mu\) sont deux nombres réels, alors \(\mathcal{C}(\lambda X + \mu Y, Z) = \lambda \mathcal{C}(X, Z) + \mu \mathcal{C}(Y, Z)\).
À retenir
Symétrie : si \(X\) et \(Y\) sont deux variables aléatoires réelles définies sur le même espace de départ, alors \(\mathcal{C}(X, Y) = \mathcal{C}(Y, X)\).
À retenir
Positivité : si \(X\) est une variable aléatoire réelle, alors \(\mathcal{C}(X, X) \geq 0\). En fait, la covariance d’une variable avec elle-même est égale à sa variance, de sorte que l’égalité n’est atteinte que pour les variables aléatoires constantes.
Une autre propriété importante de la covariance tient à son lien avec l’indépendance.
À retenir
Si \(Y\) est indépendante en moyenne de \(X\), et donc a fortiori si \(X\) et \(Y\) sont indépendantes, alors \(\mathcal{C}(X,Y)=0\).
Avertissement
La réciproque n’est en revanche pas vraie.
En effet, si \(X\) est une variable aléatoire qui vaut \(-1\) avec la probabilité \(\frac{1}{3}\), 0 avec la probabilité \(\frac{1}{3}\) et 1 avec la probabilité \(\frac{1}{3}\), et \(Y=X^2 + \frac{1}{2}\mathbf{1}_{\{1\}}(X) Z\), où \(\mathbf{1}_{\{1\}}(X)\) désigne la variable aléatoire qui vaut 1 si \(X=1\) et 0 sinon, et \(Z\) est une variable aléatoire indépendante de \(X\) de même loi que \(X\), alors \(\mathcal{C}(X,Y) = 0\), mais \(Y\) n’est pas indépendante en moyenne de \(X\), car \(\mathbb{E}[Y \mid X=1]=1\) et \(\mathbb{E}[Y \mid X=0]=0\), et \(X\) n’est pas indépendante en moyenne de \(Y\), car \(\mathbb{E}[X \mid Y=0]=0\) et \(\mathbb{E}[X \mid Y=\frac{1}{2}]=1\).
Le fragment de code suivant permet de visualiser le nuage de point généré par le tirage indépendant de 1000 couples de variables aléatoires de même loi jointe, tels que \(\mathcal{C}(X_i,Y_i)=0\) mais \(X_i\) n’est pas indépendante en moyenne de \(Y_i\) et \(Y_i\) n’est pas indépendante en moyenne de \(X_i\).
library(data.table)
library(ggplot2)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
# avoir un exemple réplicable
set.seed(651351)
#On fixe le nombre de tirages
nbr_tirages<-1000
#On tire nbr_tirages valeurs de X indépendamment avec une loi uniforme sur [-1, 1]
x_valeurs<-runif(nbr_tirages,
min=-1,
max=1)
#On tire nbr_tirages valeurs de Z indépendamment avec une loi uniforme sur [-1, 1]
z_valeurs<-runif(nbr_tirages,
min=-1,
max=1)
#On réunit les valeurs dans un data.table
table_valeurs<-data.table(x_valeurs,
z_valeurs)
#On crée les variables Y:=ZX
table_valeurs[,
y_valeurs:=x_valeurs^2 +(x_valeurs/2+1/2)*z_valeurs]
#On crée une figure agréable à l'aide du package ggplot2
ggplot(data=table_valeurs,
aes(x=x_valeurs,
y=y_valeurs))+
geom_point(color="gray")+#visualiser sour la forme d'un nuage de points
xlab("Valeur de X")+#Nom des axes
ylab("Valeur de Y")+
theme_classic()+#enlever l'arrière-plan gris par défaut
theme(text=element_text(size=16),
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))#le quadrillage léger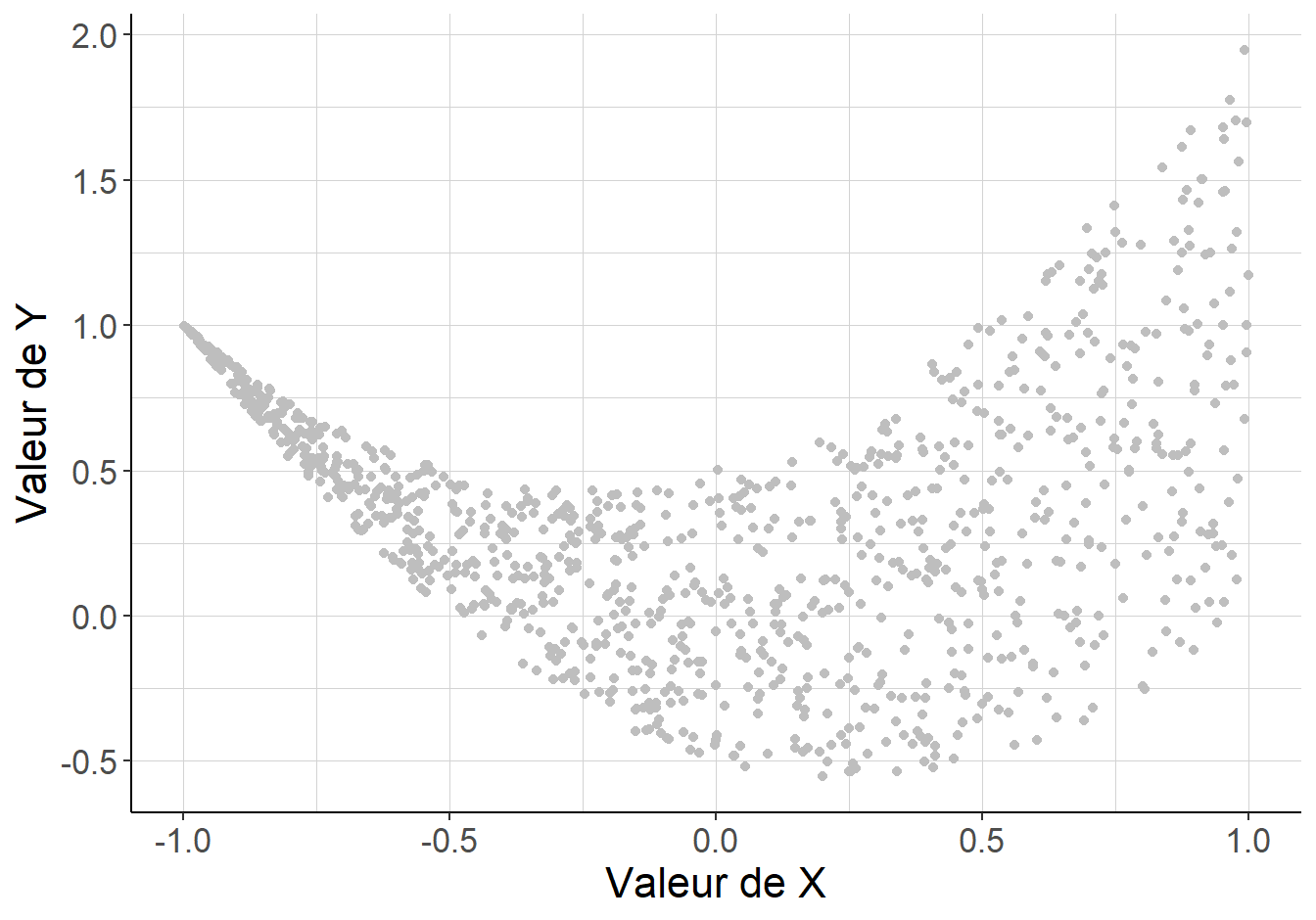
Figure 1.2: La variable aléatoire \(Y\) n’est pas indépendante en moyenne de \(X\) : son espérance conditionnelle vaut 1 si \(X=-1\) ou \(X=1\), mais 0 si \(X=0\). La variable aléatoire \(X\) n’est pas indépendante en moyenne de \(Y\) : son espérance conditionnelle vaut 1 si \(Y\) vaut 2 et \(\frac{1}{4}\) si \(Y\) vaut \(-\frac{9}{16}\). En revanche, la covariance de \(X\) et \(Y\) vaut 0.
Définition
Si \(X\) et \(Y\) sont deux variables aléatoires réelles non-constantes définies sur le même espace de départ, alors leur corrélation, notée \(\rho_{XY}\) est définie comme le rapport de leur covariance sur la racine carrée du produit de leur variances.
Formellement, cette définition s’écrit : \(\rho_{XY}:=\frac{\mathcal{C}(X,Y)}{\sqrt{\mathcal{V}(X)\mathcal{V}(Y)}}\).
Cette quantité est comprise en -1 et 1. Si \(\rho_{XY}=1\) (resp. -1), alors il existe deux nombres réels \(\alpha\) et \(\beta\), avec \(\beta\) strictement positif (resp. strictement négatif) tels que \(Y = \alpha + \beta X\). Si \(Y\) est indépendante en moyenne de \(X\), et donc a fortiori si \(X\) et \(Y\) sont indépendantes, alors leur corrélation est nulle.
1.3.6 Étude de la moyenne empirique
On peut considérer le tirage aléatoire d’un échantillon de quelques individus au sein d’une population plus grande. Soit \(n\) un entier naturel non-nul, qui correspond au nombre d’individus tirés, et soient \(X_1\) jusqu’à \(X_n\) des variables aléatoires réelles indépendantes de même loi. La variable alatoire \(X_i\) désigne ici la valeur de la variable \(X\) à laquelle on s’intéresse pour le \(i\)-ème tirage d’un individu dans la population. Comme on tire de façon équiprobable dans la population, toutes ces variables doivent avoir la même espérance, qui est essentiellement la moyenne de la variable \(X\) dans la population entière, par opposition à la moyenne dans l’échantillon que l’on vient de tirer. On peut noter \(\mathbb{E}[X]\) cette espérance. Pour la même raison, toutes les variables \(X_i\) ont la même variance \(\mathcal{V}(X)\). On peut définir la moyenne empirique sur ces tirages, c’est-à-dire la variable aléatoire \(S_n = \frac{1}{n} \sum_{i=1}^n X_i\).
La linéarité de l’espérance assure que \(\mathbb{E}[S_n] = \mathbb{E}[X]\). Par ailleurs, on peut montrer en revenant aux propriétés de bilinéarité de la covariance, et en utilisant l’indépendance des variables aléatoires \(X_1\) à \(X_n\) que \(\mathcal{V}(S_n) = \frac{1}{n} \mathcal{V}(X)\). Ainsi, la variance de la moyenne empirique \(S_n\) décroît lorsque \(n\) augmente, et tend vers 0 lorsque \(n\) tend vers l’infini. En vertu de l’inégalité de Bienaymé-Tchebychev, cela implique que la variable aléatoire \(S_n\) est d’autant plus concentrée autour de la valeur \(\mathbb{E}[X]\) que \(n\) est grand.
Le fragment de code suivant simule le comportement de la moyenne empirique du lancer d’un dés à 6 faces lorsque le nombre de lancers devient très grand.
À retenir
La moyenne empirique peut s’identifier à l’espérance lorsque le nombre d’observations tend vers l’infini. Ce résultat est connu sous le nom de loi des grands nombres.
library(ggplot2)
library(data.table)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
#avoir un exemple réplicable
set.seed(51651)
#On fixe le nombre maximal de lancers que l'on explore
nbr_lancers_max<-1000
#On génère ce nombre de lancers de dés : une variable aléatoire qui peut
#prendre de façon équiprobable n'importe quelle valeur entière de 1 à 6
lancers<-floor(runif(nbr_lancers_max,
min=1,
max=7))
#On crée une fonction qui calcule la moyenne empirique sur les nbr_lancers
#premiers lancers
moyenne<-function(nbr_lancers){
1/nbr_lancers*sum(lancers[1:nbr_lancers])
}
#On applique cette fonction pour tous les entiers de 1 jusqu'à nbr_lancers_max
# et on stocke les résultats dans un data.table
moyenne_nbr_lancers<-data.table(unlist(lapply(FUN=moyenne,
1:nbr_lancers_max)))
#Quelques opérations simples sur le data.table pour avoir
# 1. une variable dans laquelle on stocke le nombre de lancers correspondant au
# calcul de la moyenne empirique
# 2. un nom de variable plus explicite
moyenne_nbr_lancers[,
nbr_lancers:=.I]
colnames(moyenne_nbr_lancers)[1]<-c("moyenne_empirique")
#On crée une figure agréable à l'aide du package ggplot2
ggplot(data=moyenne_nbr_lancers,
aes(x=nbr_lancers,
y=moyenne_empirique))+
geom_point()+#visualiser sour la forme d'un nuage de points
coord_cartesian(ylim=c(1,6),
xlim=c(1,nbr_lancers_max))+#fixer l'échelle des axes
xlab("Nombre de lancers")+#Nom des axes
ylab("Moyenne empirique")+
geom_hline(yintercept=3.5,
color="red")+#une ligne rouge pour l'espérance
annotate("text",
x=3*nbr_lancers_max/4,
y=3.25,
label="Espérance : 3.5",
size=4,
color="red")+#Donner un label à la ligne rouge
theme_classic()+#enlever l'arrière-plan gris par défaut
theme(text=element_text(size=16),
strip.text.x = element_text(size=16),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))#le quadrillage léger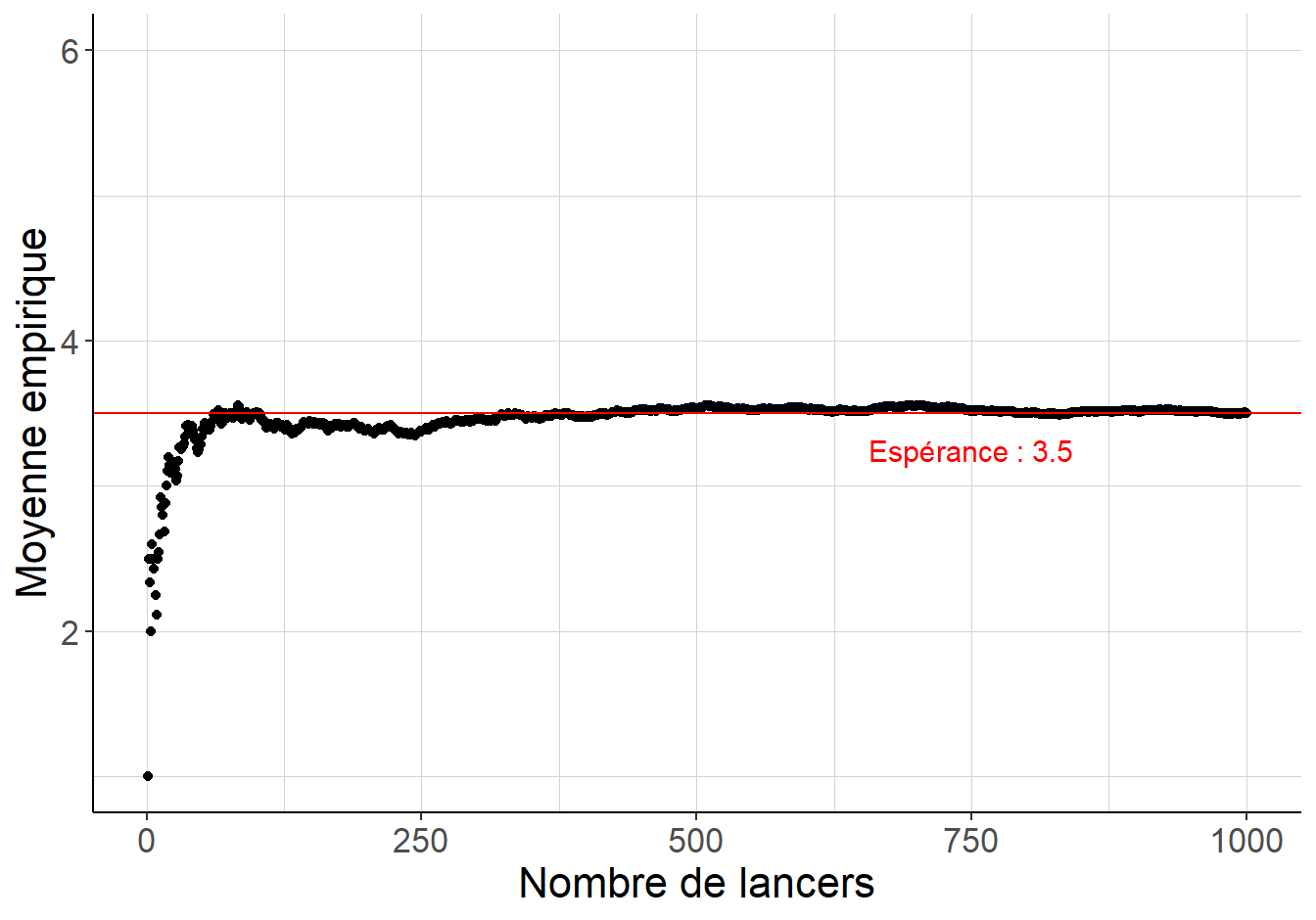
Figure 1.3: Lorsque le nombre de lancers simulés devient très grand, la moyenne empirique des résultats des lancers d’un dé équilibré à 6 faces s’identifie à l’espérance \(\frac{1+2+3+4+5+6}{6}=3.5\).
Ce résultat sert de fondement à la très grande majorité des outils statistiques usuels. C’est essentiellement lui qui justifie l’existence d’un lien entre les quantités observables dans des données, généralement en échantillon fini, et des quantités impossibles ou très difficiles à observer directement, par exemple parce qu’elles portent sur la population exhaustive ou qu’elles font intervenir un modèle théorique plus ou moins explicite.
C’est ainsi en vertu de ce résultat qu’il n’est pas dénué de sens de parler à la fois de l’écart-type empirique d’une variable, c’est-à-dire de l’écart-type mesuré directement à partir de données observées sur un échantillon fini, et de l’écart-type de la variable correspondant dans la population totale. En effet, le premier, calculé à partir de moyennes empiriques peut s’identifier lorsque la taille de l’échantillon devient suffisamment grande au second qui s’exprime à l’aide d’espérances.
Le résultat précédent peut par ailleurs encore être raffiné : on peut montrer que lorsque \(n\) tends vers l’infini, la loi de la variable aléatoire \(\sqrt{\frac{n}{\mathcal{V}(X)}} \{S_n - \mathbb{E}[X]\}\) s’identifie à la loi normale centrée (c’est-à-dire d’espérance nulle) réduite (c’est-à-dire d’écart-type égal à 1). Ce résultat est appelé théorème central limite. Il est particulièrement utile pour quantifier l’incertitude liée à l’utilisation de la moyenne empirique \(S_n\) comme estimateur de l’espérance \(\mathbb{E}[X]\). En effet, pour \(n\) suffisamment grand, il permet d’approximer la distribution de \(S_n\). Il est en particulier utilisé pour de nombreux résultats ayant trait à la construction d’intervalles de confiance ou de tests statistiques.
Le fragment de code suivant permet de visualiser sous la forme d’un histogramme la distribution des valeurs de 10000 calculs indépendants de la moyenne empirique d’un certain nombre \(n\) de lancers d’un dé à 6 faces, et de la comparer à la distribution attendue pour une variable aléatoire de loi normale d’espérance 3.5 et de variance \(\frac{1}{n} \mathcal{V}(X)\). On perçoit bien que (i) les distributions se resserrent autour de l’espérance égale à 3.5 à mesure que le nombre de lancers augmente, et (ii) que la qualité de l’approximation par la loi normale s’améliore à mesure que le nombre de lancers devient très grand.
library(ggplot2)
library(data.table)
#On commence par fixer le générateur de nombres pseudo-aléatoires pour
#avoir un exemple réplicable
set.seed(51651)
#On fixe le nombre de calculs de la moyenne empirique que l'on va étudier
nbr_moyennes<-10000
#On calcule l'espérance et l'écart-type de la variable aléatoire correspondant
# au lancer d'un dé
esperance<-(1+2+3+4+5+6)/6
ecarttype<-sqrt((1+2^2+3^2+4^2+5^2+6^2)/6-esperance^2)
#On crée une fonction qui
# 1. génère nbr_moyennes échantillons de lancers de dé, chacun de taille nbr_lancers
# 2. calcule la moyenne empirique pour chacun de ces échantillons
# 3. représente la distribution de ces moyennes empiriques sous la forme
# d'un histogramme
histo_moyennes<-function(nbr_lancers){
#On génère les lancers de dés : des variables aléatoires qui peuvent
#prendre de façon équiprobable n'importe quelle valeur entière de 1 à 6
# et on les stocke dans un data.table
lancers<-data.table(floor(runif(nbr_moyennes*nbr_lancers,
min=1,
max=7)))
#On attribue à chaque lancer son numéro d'ordre
lancers[,
id_lancer:=.I]
#On renomme la variable
colnames(lancers)[1]<-"resultat"
#On calcule les moyennes empiriques
moyennes<-lancers[,
list(moyenne=mean(resultat)),
by=floor((id_lancer-1)/nbr_lancers)]
#On crée une figure agréable à l'aide du package ggplot2
figure<-ggplot(data=moyennes,
aes(x=moyenne))+
geom_histogram(alpha=0.5,
bins=100,
aes(y=0.01*..density..))+#visualiser un histogramme
geom_function(fun = function(x)
0.01*
(sqrt(nbr_lancers)/ecarttype)*
1/sqrt(2*pi)*
exp(-1/2*((x-esperance)/(ecarttype/sqrt(nbr_lancers)))^2),
color="red")+
#Densité de la loi normale de même espérance et de même variance
coord_cartesian(#ylim=c(0,0.1),
xlim=c(max(1,
3.5-1/sqrt(nbr_lancers)*1.707825*4),
min(6,
3.5+1/sqrt(nbr_lancers)*1.707825*4)))+#échelle des axes
scale_y_continuous(labels = scales::percent)+#Mesurer la fréquence en %
xlab("Moyenne empirique")+#Nom des axes
ylab("Fréquence relative")+
annotate("text",
x=min(3.5+2.5/sqrt(nbr_lancers)*1.707825),
y=0.75*0.01*1/(1.707825/sqrt(nbr_lancers)*sqrt(2*pi)),
label=paste0(nbr_lancers,
" lancers"),
size=6)+#Donner un label à chaque figure
theme_classic()+#enlever l'arrière-plan gris par défaut
theme(text=element_text(size=32),
strip.text.x = element_text(size=32),
panel.grid.minor = element_line(colour="lightgray",
linewidth=0.01),
panel.grid.major = element_line(colour="lightgray",
linewidth=0.01))#le quadrillage léger
print(figure)
}
histo_moyennes(5)## Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(density)` instead.histo_moyennes(1000)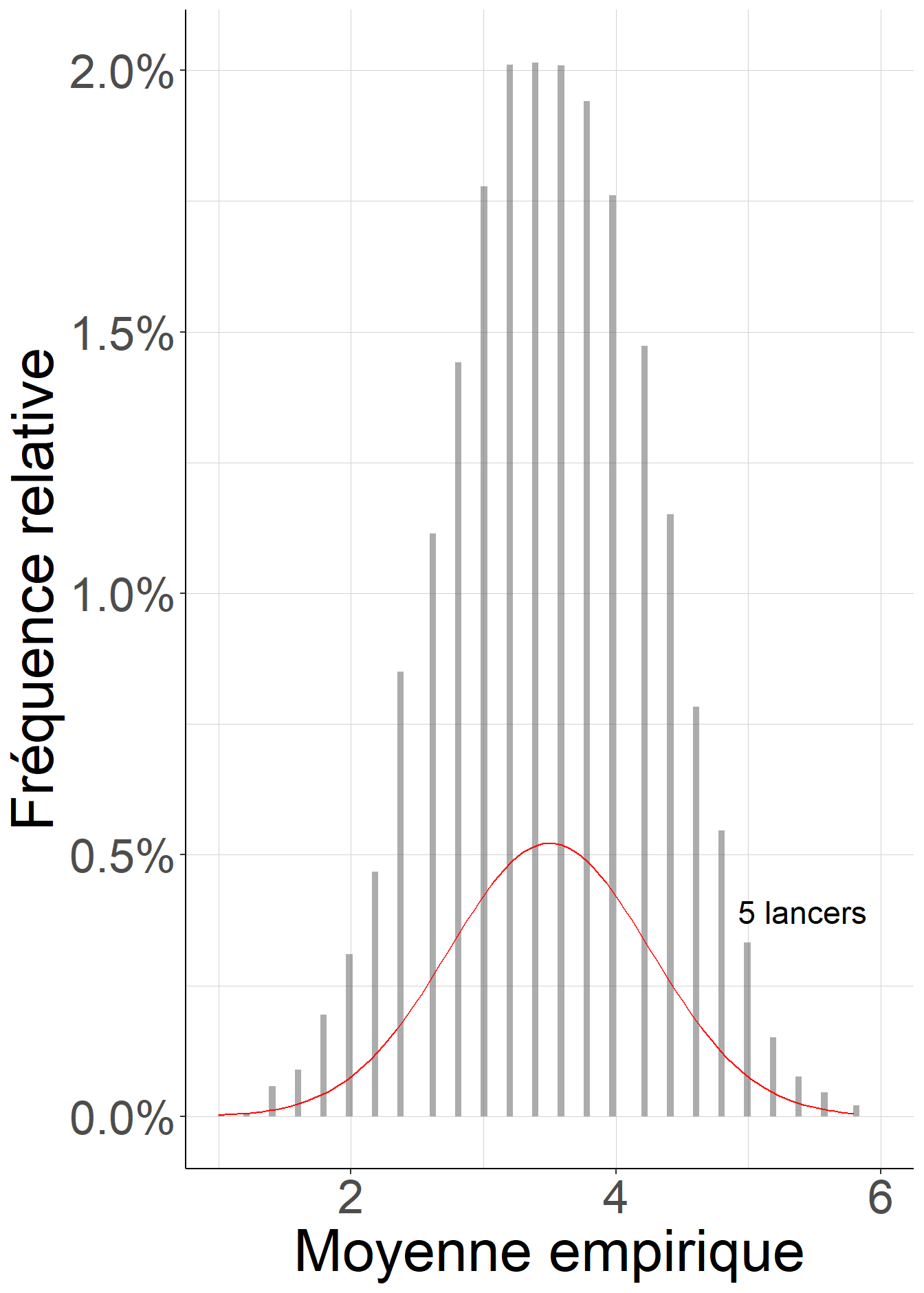
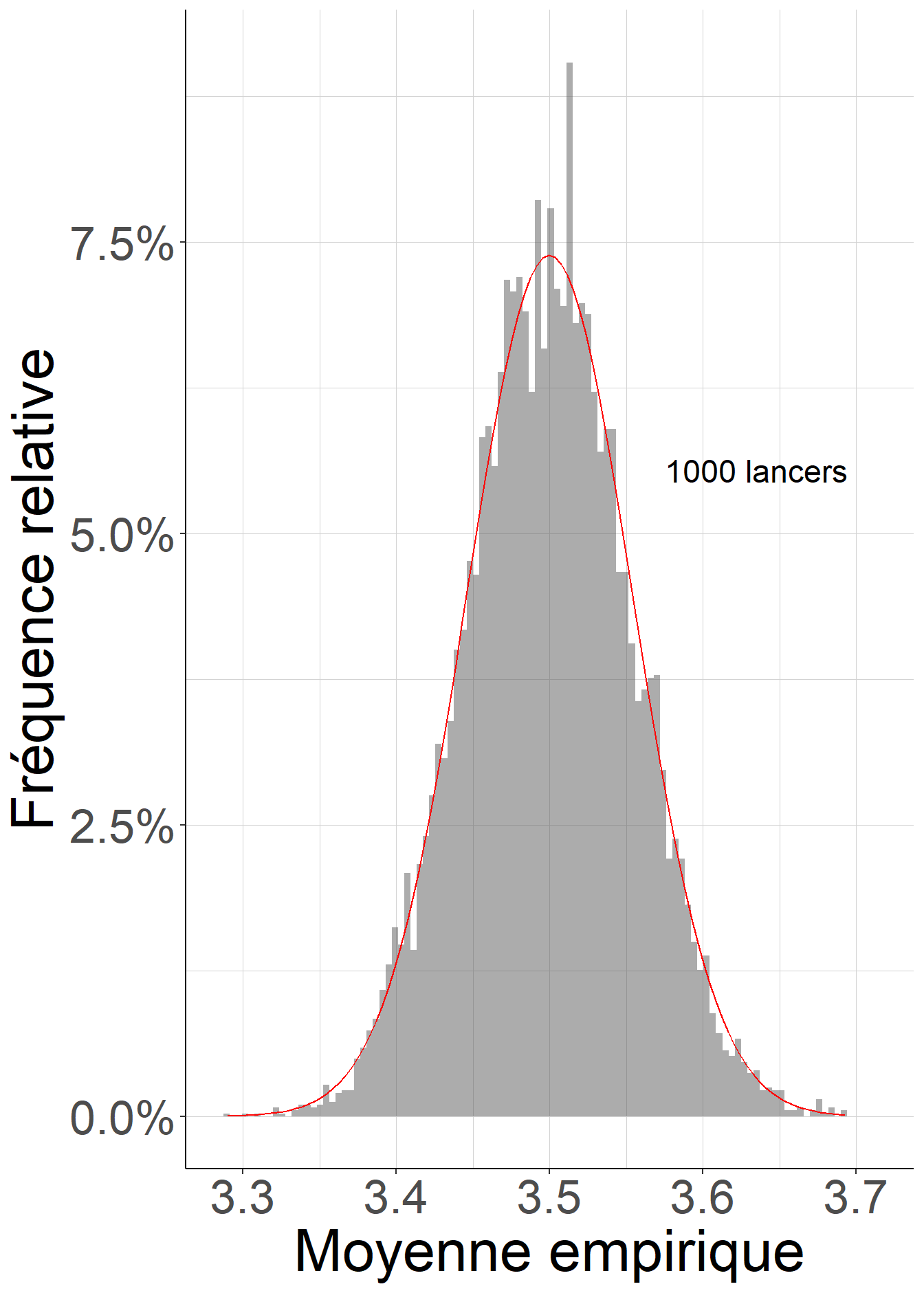
Figure 1.4: Lorsque le nombre de lancers devient très grand, la distribution des moyennes empiriques est de plus en plus concentrée autour de l’espérance, et est de mieux en mieux approximée par une loi normale.